10.2.2. Поверхностные явления

В отличие от газов жидкости имеют поверхность, отделяющую их от другой (например, газовой) фазы. Рассмотрим явления, происходящие на этой поверхности раздела.

Рис. 10.8

Силы взаимодействия между молекулами жидкости быстро убывают по мере увеличения расстояния между ними, т.е. они короткодействующие. В связи с этим можно считать, что некоторая молекула, выделенная внутри жидкости, взаимодействует лишь с ограниченным числом ближайших соседей, попадающих внутрь сферы радиуса R (радиуса взаимодействия) – на расстояниях r > R взаимодействие отсутствует.

Если сфера взаимодействия лежит внутри жидкости, то в силу изотропности свойств жидкости результирующая сила, действующая на молекулу, равна нулю (рис. 10.8, а). Если же сфера взаимодействия частично выходит за пределы жидкости, то полной компенсации не будет – возникнет результирующая сила, направленная в глубь жидкости (рис. 10.8, б, в). Таким образом, результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, которое называется внутренним (или межмолекулярным).

Рис. 10.9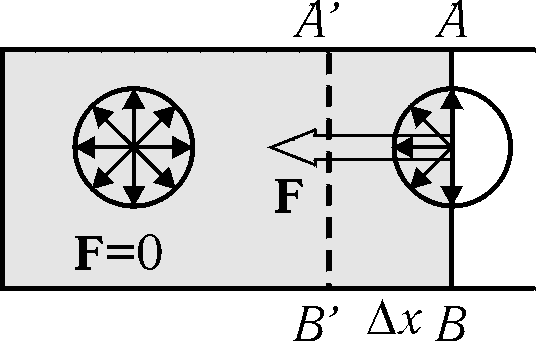

Рассмотрим теперь тонкую пленку жидкости, натянутую на неподвижный проволочный каркас прямоугольной формы (рис. 10.9). Сфера взаимодействия вырезает на поверхности пленки круг радиусом R. Если этот круг расположен полностью внутри пленки, то суммарная сила, действующая на выделенную молекулу, равна нулю. Иная ситуация складывается для молекулы, находящейся на границе раздела "жидкость-воздух": здесь круг взаимодействия частично выходит за пределы жидкости (рис. 10.9). В результате возникает не скомпенсированная сила, направленная в глубь жидкости перпендикулярно к линии раздела, и касательная поверхности жидкости.

Суммарная сила F, действующая на все молекулы, находящаяся на границе раздела "пленка-воздух", пропорциональна числу молекул N, которое, в свою очередь, пропорционально длине l линии раздела. Таким образом,

,

(10.6)

где  – коэффициент поверхностного натяжения.

Из (10.6) видно, что коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины линии раздела и направленной в глубь пленки перпендикулярно к линии раздела.

Если граница раздела АВ (рис. 10.9) не закреплена, то под действием силы поверхностного натяжения эта граница будет перемещаться и спустя некоторое время займет положение A'B'. Работа этой силы

,

Рис. 10.10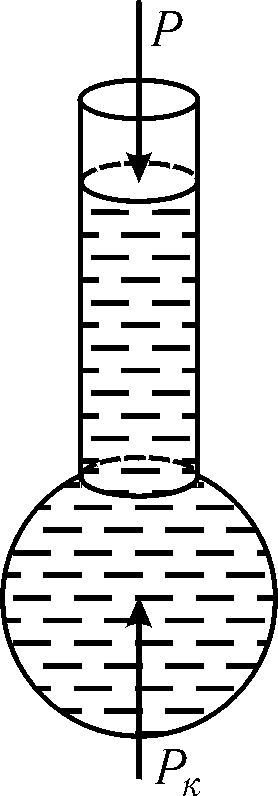

или

,

(10.7)

где  – изменение площади пленки жидкости. Из (10.7) можно дать другое определение коэффициента поверхностного натяжения как работы, которую совершают поверхностные силы по изменению площади свободной поверхности жидкости на единицу.

Если поверхность раздела искривлена, то силы поверхностного натяжения приводят к возникновению дополнительного капиллярного давления. Чтобы получить выражение для капиллярного давления, рассмотрим вертикальную трубку, заполненную жидкостью (рис. 10.10). На конце трубки образуется капля, имеющая в первом приближении сферическую форму. Жидкость в трубке находится в состоянии равновесия, поскольку гидростатическое давление компенсируется капиллярным давлением P_K, возникающим под искривленной поверхность жидкости.

Чтобы увеличить объем висящей капли, необходимо совершить работу против капиллярных сил:

.

(10.8)

Эта работа будет затрачена на увеличение свободной поверхности капли

.

(10.9)

Приравнивая (10.8) к (10.9) и учитывая, что для капли , а , получаем

.

(10.10)

Отметим, что капиллярное давление направлено всегда по радиусу кривизны поверхности к ее центру и может быть весьма значительным, если радиус кривизны поверхности мал.

Капиллярное давление играет значительную роль в процессах смачивания, растекания и капиллярного подъема.

Лекція 18.

Загальна характеристика фазових переходiв. Фазовий перехiд першого роду. Рiвняння Клапейрона-Клаузiуса. Фазовi переходи другого роду.