10.1.4. Теоретические изотермы реальных газов (изотермы Ван-дер-Ваальса)

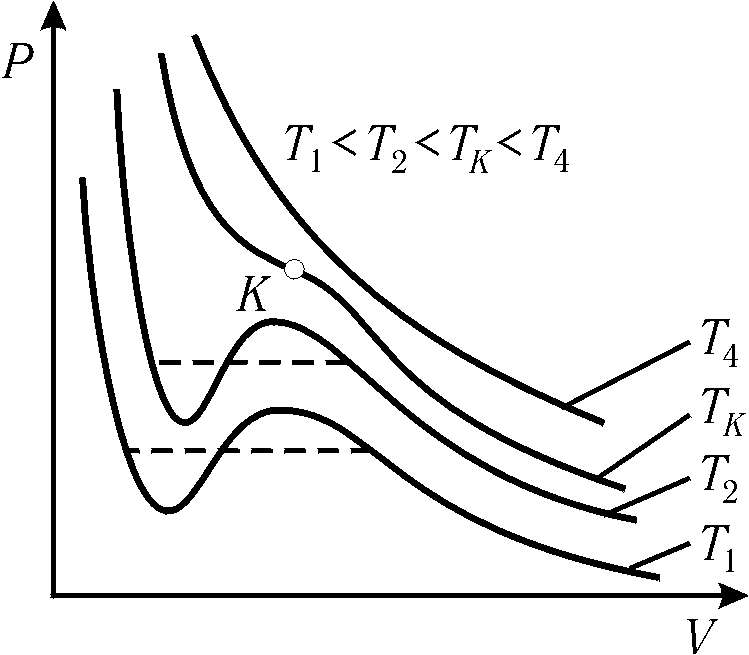
На рис. 10.6 показано семейство изотерм реального газа, рассчитанных по уравнению Ван-дер-Ваальса. В области высоких температур они достаточно близки к экспериментальным. При более низких температурах на теоретических изотермах появляется характерный "завиток", отражающий некоторые детали процессов сжижения газов и испарения жидкостей.

Рис. 10.6

Рис. 10.7

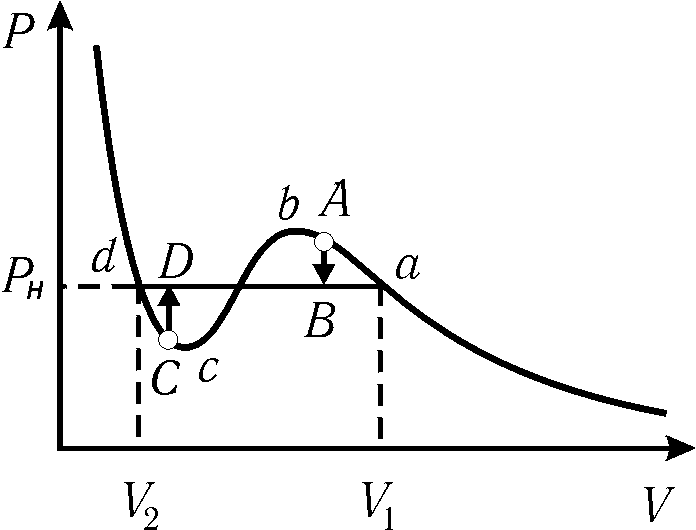
Рассмотрим подробнее этот участок.

При сжатии реального газа до объема V₁ (рис. 10.7) обычно начинается его сжижение. Однако если газ очищен от примесей (пылинок, ионов и т.д.), которые могут являться центрами конденсации, он может оставаться в газовом состоянии при давлениях, более высоких по сравнению с давлением насыщенного пара – точка А на рис. 10.7. Такое состояние называется пересыщенным паром и является метастабильным (малоустойчивым) – при внесении в него центров конденсации сразу же происходит переход в более устойчивое двухфазное состояние (переход А  В). Аналогичная картина наблюдается при переходе из жидкого состояния в двухфазное. Чистая жидкость, в которой отсутствуют центры парообразования, может переходить в растянутое (перегретое) малоустойчивое состояние – участок dc на рис. 10.7.

Участок cb изотермы Ван-дер-Ваальса, на котором увеличению давления соответствует увеличение объема, принципиально неустойчив и реализован быть не может.

Следует отметить, что оба метастабильных состояния вещества находят практическое применение при регистрации микрочастиц (камера Вильсона, пузырьковая камера).

10.1.5. Расчет критических параметров вещества из уравнения Ван-дер-Ваальса

На рис. 10.5 пунктиром показаны границы, разделяющие семейство изотерм Ван-дер-Ваальса на области газообразного (I), жидкого (II) и двухфазное состояние (III). Все эти области имеют общую точку К, которая является критической и совпадает с точкой перегиба критической изотермы.

Уравнения Ван-дер-Ваальса является уравнением третьей степени относительно объема и может быть представлено в виде

.

(10.3)

Как известно алгебраическое уравнение третьей степени имеет три корня, которые могут быть либо все действительными, либо один действительный, а два комплексно сопряженными. В критической точке уравнение Ван-дер-Ваальса имеет три действительных совпадающих корня, соответствующих значению критического объема V_K. Пользуясь теоремой Виета, уравнение Ван-дер-Ваальса можно записать в виде

или

(10.4)

Сравнивая коэффициенты при различных степенях V в уравнениях (10.3) и (10.4), можно получить систему уравнений относительно критических параметров

Из этой системы следует

.

(10.5)

Результаты расчетов по формуле (10.5) достаточно близки к опытным значениям критических параметров.

Лекція 17.

10.2. Жидкое состояние

10.2.1. Общие представления. Характер теплового движения молекул жидкости

Согласно представлениям, изложенным в предыдущем параграфе, жидкое состояние по своим свойствам близко к газообразному, отличаясь от него в первую очередь большей плотностью, т.е. меньшим межмолекулярным расстоянием. Однако такие представления не совсем точны, поскольку жидкое состояние существенно ближе к твердому (кристаллическому) состоянию. Об этом свидетельствует следующее:

• плотность жидкости и ее теплоемкость близки к соответствующим значениям для твердых тел;

• теплота испарения значительно выше теплоты плавления;

• экспериментально показано существование в жидкости определенного порядка в расположении молекул, сходного по ряду параметров с упорядоченностью, характерной для твердых тел.

Для жидкостей глубина потенциальной ямы межмолекулярного взаимодействия (см. рис. 10.1) сравнима с энергией хаотического теплового движения (kT), что обусловливает колебательно-поступательный характер теплового движения молекул жидкости. Находясь в некотором равновесном положении, молекула жидкости колеблется с частотой 10¹³ Гц. За время жизни в положении равновесия    10^‑8 c (время "оседлости") молекула успевает совершить в среднем 10⁵ колебаний, а затем переходит в новое положение равновесия. С повышением температуры растет средняя кинетическая энергия молекул и, кроме того, вследствие расширения жидкости в ней растет число пустых мест (вакансий). Эти факторы облегчают переход молекулы из одного положения равновесия в другое.

Время "оседлой" жизни молекул зависит от температуры

,

где W – энергия, необходимая для перехода молекулы из одного равновесного положения в другое (энергия активации).

Такой характер теплового движения молекул жидкости определяет их механические свойства. При кратковременных воздействиях (t < ) жидкости ведут себя как хрупкие твердые тела. Такой случай реализуется при прохождении через жидкость упругих ультразвуковых волн. При более длительных воздействиях жидкости текут и в них создаются силы сопротивления истечению – силы вязкости (внутреннего трения).