2. Статистический смысл второго начала термодинамики

Для того чтобы глубже уяснить суть второго начала термодинамики, обратимся к представлениям статистической физики.

Термодинамическая система может находиться в различных микросостояниях, которым соответствуют различные распределения молекул по скоростям, энергиям, координатам и т.д. Одному и тому же макросостоянию системы, находящейся в термодинамическом равновесии, вообще говоря, соответствует множество микросостояний. Термодинамически равновесная система может самопроизвольно переходить из одного микросостояния в другое, однако макроскопическое состояние, характеризуемое параметрами P, V, T и т. д., при этом не меняется

Пусть в течение некоторого достаточно длительного промежутка времени наблюдения за системой i-е микроскопическое состояние реализовывалось N_i раз. Тогда вероятность i-го микросостояния определяется как соотношение , где N – общее число микросостояний, которое реализовалось за время наблюдения.

Рис. 9.11

Рассмотрим теперь в качестве простейшей модели термодинамической системы идеальный газ, состоящий из двух молекул а и b. Разделим объем, в котором заключен газ, на две равные ячейки и рассмотрим возможные распределения молекул. Очевидно, что возможно четыре распределения (рис. 9.11) с вероятностью каждого из них. Микросостояния 1 и 2 соответствуют равномерному распределению газа по всему объему и являются эквивалентными. Следовательно, вероятность состояния, в котором газ равномерно распределен по всему объему , т.е. равна веро­ят­ности отдельного распределения на число способов, которыми может быть осуществлено это распределение.

Число способов, с помощью которых реализуется данное состояние системы, называется термодинамической вероятностью состояния. Таким образом, в рассматриваемом примере термодинамическая вероятность состояния, в котором газ равномерно распределен по всему объему, равна двум.

По мере увеличения числа молекул термодинамическая вероятность их равномерного распределения по всему объему быстро возрастает. Так, для газа, состоящего из четырех молекул a, b. c, d, возможны шесть эквивалентных микросостояний, в которых газ равномерно распределен по всему объему сосуда. Это состояния ab - cd, ac - bd, ad - bc, bc - ad, bd - ac, cd ‑ ab. Для газа, состоящего из шести молекул, термодинамическая вероятность состояния, в котором газ равномерно заполняет весь объем, возрастает до 20 и т.д. В то же время, независимо от числа молекул, термодинамическая вероятность состояния, в котором газ занимает одну из половинок сосуда, остается постоянной и равной двум.

Проделаем теперь следующий мысленный эксперимент: пусть в исходном состоянии газ находится в одной из половинок сосуда, отделённой от другой половинки непроницаемой перегородкой. Такое состояние газа характеризуется термодинамической вероятностью Р₁=2. Уберём теперь перегородку. Спустя некоторое время мы обнаружим, что газ более или менее равномерно распределён по всему объёму сосуда (рис. 9.12). Такое состояние газа характеризуется термодинамической вероятностью Р₂>Р₁. Таким образом, в системе произошёл процесс в сторону возрастания термодинамической вероятности состояния. Обратный процесс маловероятен, поскольку из огромного числа различных способов размещения молекул лишь два из них соответствуют состоянию, когда газ самопроизвольно соберётся в одной половине сосуда.

Рис. 9.12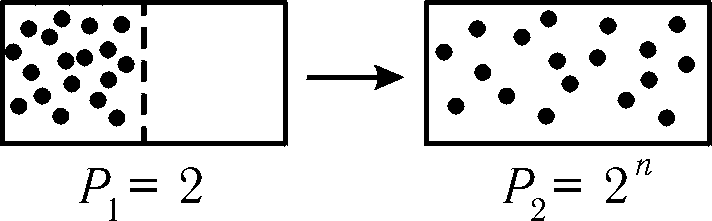

Такое поведение термодинамической вероятности состояния довольно общее и позволяет дать более глубокое понятие об обратимых и необратимых процессах.

Обратимым называется такой процесс, в котором начальное и конечное состояния характеризуются одинаковым значением термодинамической вероятности. Вероятность протекания обратимого процесса в прямом и обратном направлениях одинакова.

Необратимым называется такой процесс, обратный которому маловероятен.

С помощью понятия термодинамической вероятности состояния можно переформулировать второе начало термодинамики следующим образом: все процессы в изолированной системе могут протекать в таких направлениях, когда термодинамическая вероятность состояния не убывает.

Аналогичным образом ведёт себя энтропия, поэтому между термодинамической вероятностью состояния и энтропией должна быть связь. Эта связь была установлена Больцманом (1872 г.) и имеет вид:

,

(9.48)

где k ­ – постоянная Больцмана.

Согласно формуле Больцмана можно дать определение энтропии как меры вероятности осуществления какого-либо макросостояния.