4. Идеальная тепловая машина Карно

Рис. 9.8

В 1927 г. французский военный инженер С. Карно, решая вопрос о рациональной конструкции тепловой машины, повышения ее КПД, предложил циклический процесс, названный его именем.

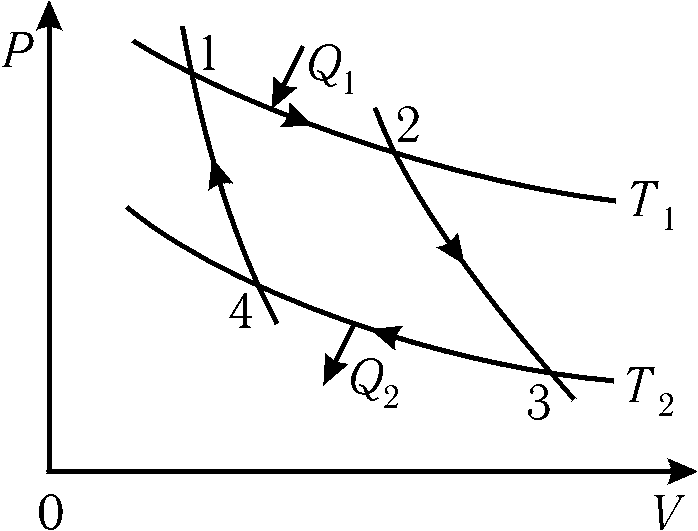
Цикл Карно состоит из двух адиабат и двух изотерм (рис. 9.8). На этом рисунке 12 – изотермическое расширение при температуре T₁; 23 адиабатное расширение; 34 – изотермическое сжатие при температуре T₂; 41 – адиабатное сжатие. Точки цикла 1-4 характеризуются параметрами: 1 (P₁, V₁, T₁); 2 (P₂, V₂, T₁); 3 (P₃, V₃, T₂); 4 (P₄, V₄, T₂).

В идеальной машине Карно пренебрегают такими источниками потерь, как трение между цилиндром и поршнем, утечка теплоты через стенки цилиндра. Можно показать, что КПД тепловой машины не зависит от природы рабочего тела. Как пример, в качестве рабочего тела возьмём идеальный газ.

Работа, выполненная тепловой машиной Карно за один цикл, очевидно равна алгебраической сумме работ на отдельных ее участках:

,

(9.25)

Значения работ на участках 2–3 и 4–1 равны по величине и противоположны по знаку, т.е. A₂₃+A₄₁=0, поэтому

,

(9.26)

Так как при изотермических процессах 12 и 34 теплота в соответствии с первым началом термодинамики полностью расходуется на выполнение работы, то

;	(9.27)
;	(9.28)
.	(9.29)

В выражении (9.28) Q₂ взято со знаком "-", так как в процессе 34 теплота отводится от рабочего тела к холодильнику.

С учетом (9.27)–(9.29) выражение для суммарной работы (9.26) можно представить в виде

.

(9.30)

КПД цикла Карно, как и любой другой тепловой машины, можно найти по (9.24). Поэтому, подставляя (9.27) и (9.30) в (9.24), получаем

.

(9.31)

Поскольку процессы 23 и 41 адиабатные, то для них на основании (9.22) можно записать:

;
.

Разделив эти выражения, приходим к условию замкнутости цикла:

.

(9.32)

С учётом (9.32) выражение для КПД цикла Карно (9.31) упрощается:

(9.33)

или

.

(9.34)

Как видно из (9.34), даже у такого предельно идеализированного цикла КПД меньше единицы. Он может стать равным единице только в случаях Т₁ или Т₂=0, что нереализуемо. Как видно из (9.34), практический путь повышения КПД – это повышение температуры нагревателя, что используется в технике при конструировании тепловых машин последующих поколений.

Можно показать, что КПД цикла Карно выше КПД любой другой тепловой машины:

.

(9.35)

Качественно это неравенство можно пояснить тем, что использование изотермического процесса в цикле Карно сопровождается наиболее эффективным превращением теплоты в работу. Кроме того, при адиабатных процессах 23 и 41 (см. рис. 9.8) теплота не уходит из рабочего тела в окружающую среду.

Лекція 15.