Первое начало термодинамики и его применение к изопроцессам

Первое начало термодинамики – это обобщение закона сохранения энергии с учетом тепловых процессов. Его формулировка: количество теплоты, сообщенное системе, расходуется на выполнение работы против внешних сил и изменение ее внутренней энергии:

.

(9.3)

Первому началу термодинамики можно дать другую формулировку, если учесть, что , т.е.

.

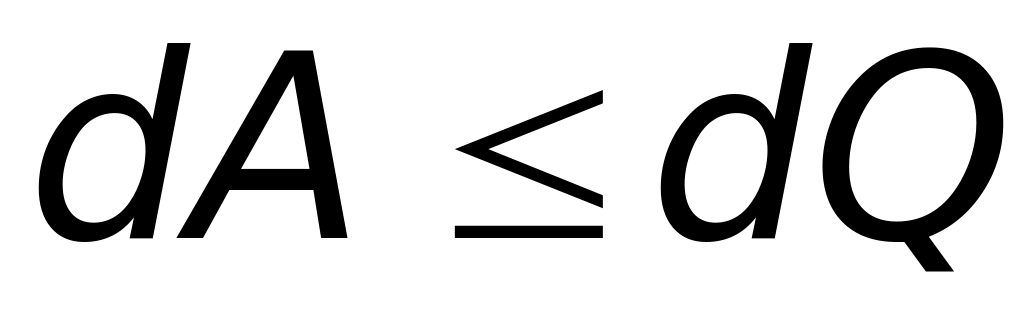(9.4)

На основании (9.4) первое начало термодинамики можно сформулировать следующим образом: невозможно построить двигатель, который совершал бы работу большую, чем количество затраченной теплоты.

Применим первое начало термодинамики к различным изопроцессам.

1. Изохорный процесс. В этом процессе объем остается постоянным, поэтому dA=PdV=0 и

.

В изохорном процессе теплота, подведенная к системе, полностью расходуется на изменение ее внутренней энергии.

2. Изобарный процесс. Так как объем изменяется, то при подведении теплоты к системе она частично превращается в работу и поэтому первое начало термодинамики имеет вид

.

Вычислим согласно (9.2) работу, совершаемую системой при изобарном процессе (P=const)

,

(9.5)

3. Изотермический процесс. При постоянной температуре изменение внутренней энергии идеального газа не происходит – dU=0, поэтому

.

В изотермическом процессе вся теплота, подведенная к газу, расходуется на совершение работы.

Поскольку Pconst, то в (9.2) его нельзя выносить за знак интеграла. Выразим давление P через объем V с помощью уравнения Менделеева-Клапейрона:

.

(9.6)

Подставим (9.6) в (9.2) и вынесем постоянные за знак интеграла

,

откуда

.

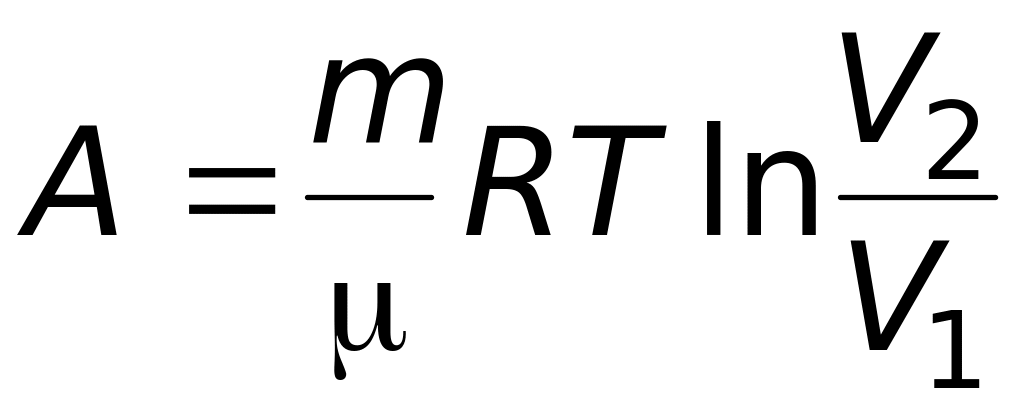9.3. Число степеней свободы. Внутренняя энергия идеального газа

Рис. 9.4

Числом степеней свободы называется число независимых координат, которыми описывается движение тела в пространстве. Материальная точка имеет три степени свободы, поскольку при ее движении в пространстве изменяются три координаты x, y, z. Система из двух материальных точек, расстояние между которыми остается постоянным, имеет пять степеней свободы: три из них приходится на поступательное движение и две – на вращательное (рис. 9.4) вокруг осей x и z. Вращение вокруг оси y не дает дополнительной степени свободы, так как при этом положения материальных точек в пространстве не изменяется.

Средняя кинетическая энергия поступательного движения молекулы равна  – формула (8.12). Это движение можно рассматривать как движение с тремя степенями свободы, поскольку молекулы идеального газа можно принять как материальные точки. Все три степени свободы равноправны, поэтому можно считать, что на одну степень свободы приходится энергия

.

(9.8)

В статистической физике доказывается, что на любую степень свободы движения молекулы (поступательную, вращательную и т.д.) приходится одна и та же энергия, равная . Это утверждение носит название закона распределения энергии по степеням свободы.

В общем случае, когда молекула имеет i степеней свободы, ее кинетическая энергия

.

(9.9)

Подсчитаем теперь внутреннюю энергию одного киломоля идеального газа. Эта энергия может быть найдена умножением средней энергии одной молекулы на их число, т.е. число Авогадро:

.

Поскольку kN_A=R, где R – универсальная газовая постоянная, то

.

(9.10)

Из (9.10) видно, что внутренняя энергия идеального газа полностью определяется его температурой.

Лекція 14.

Класична теорiя теплоємностi газiв. Адiабатний процес.Оборотнi та необоротнi процеси. Круговi процеси (цикли). Принцип дiї теплової машини. Ідеальна теплова машина Карно.