2. Молекулярно-кинетическая теория явлений переноса

В явлениях переноса каждая молекула переносит от слоя к слою некоторую физическую микроскопическую величину a: среднюю энергию движения в явлении теплопроводности – ; массу в явлении диффузии – a=m₀; импульс направленного движения в явлении вязкости – a=mu (см. табл. 8.1)

Рис. 8.11.

Задача молекулярно-кинетической теории состоит в установлении связей между макроскопическими характеристиками явлений переноса dG и микрохарактеристиками a. Для установления этой связи вычислим поток физической величины a через площадку S. На расстоянии, равном длине свободного пробега , слева и справа расположим еще две такие же площадки (рис. 8.11). В месте расположения этих площадок значения физических величин a₁ и a₂, переносимых молекулами, различны. В общем случае различны также скорости хаотического движения молекул ( и ), а в случае явления диффузии – концентрация примесных молекул (n₁ и n₂). Однако, поскольку скорость хаотического движения молекулы меняется с температурой очень медленно, (  ~  см. формулу (8.18)), то можно считать, что .

Поскольку расстояние между площадками равно длине свободного пробега, то молекулы проходят его без столкновений. Очевидно, что поток физической величины a можно найти, умножив a на число молекул dN, пересекающих центральную площадку за время dt:

,

где dN определяется формулой (8.4).

Поток слева направо: ;

поток справа налево: .

Суммарный поток определяется разностью

.

(8.35)

Формула (8.35) – основная при рассмотрении конкретных явлений переноса.

1. Явление теплопроводности. В этом случае (см. табл. 8.1)

,

поэтому из формулы (8.35) следует

.

В явлении теплопроводности основную роль играет перепад температур, поэтому можно считать, что значения концентраций n₁ и n₂ одинаковы: n₁=n₂=n. В связи с этим

.

(8.36)

Выразим разность температур T₁-T₂ через ее градиент:

.

(8.37)

где вместо dx взято расстояние между крайними площадками, равное .

С учетом (8.37) выражение (8.36) принимает вид

.

(8.38)

Полученное уравнение совпадает с уравнением теплопроводности (8.31). Из сопоставления этих уравнений находим коэффициент теплопроводности

.

(8.39)

2. Явление диффузии. Для основного газа поток dG=0, поскольку концентрация этого газа распределена по объему равномерно: n₁=n₂=n. Поэтому в выражении (8.35) мы должны учесть лишь поток, вызванный молекулами примеси. Положив в этом случае a₁=a₂=m₀ и заменив концентрации основного газа n₁ и n₂ на концентрации примеси n₁₀ и n₂₀, из формулы (8.35) получим

.

(8.40)

где _-_=n₁₀m₀-n₂₀m₀ – разность плотностей примесного газа, как и в предыдущем случае, можно выразить через градиент

.

(8.41)

Подставим (8.41) в (8.40):

.

Полученное уравнение совпадает с уравнением диффузии (8.32). Из сопоставления этих уравнений находим коэффициент диффузии

.

(8.42)

3. Явление вязкости. В этом случае (табл. 8.1) dG=dK, a₁=mu₁, a₂=mu₂, поэтому уравнение (8.35) принимает вид

.

(8.43)

В явлении вязкости основную роль играет перепад скорости направленного движения, поэтому n₁=n₂=n и уравнение (8.43) принимает вид

.

Снова, как и в явлении теплопроводности, выразим разность через соответствующий градиент:

.

Тогда

.

Полученное уравнение совпадает с уравнением вязкости (8.33). Из сопоставления этих уравнений можно найти коэффициент вязкости

.
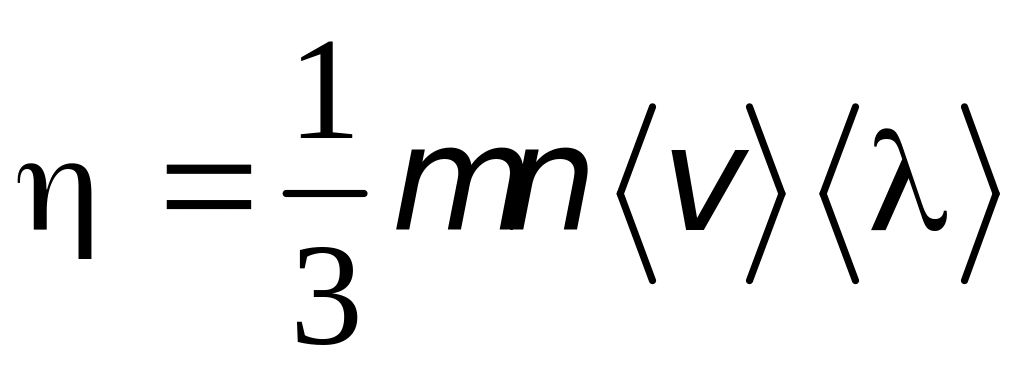