3. Барометрическая формула

Рассмотрим поведение идеального газа в поле силы тяжести. Как известно, по мере подъема от поверхности Земли давление атмосферы уменьшается. Найдем зависимость давления атмосферы от высоты над уровнем моря, используя следующую упрощенную модель.

1. Температура газа и его молекулярный состав не зависят от высоты.

2. Ускорение свободного падения на всех высотах, где существует атмосфера, постоянно.

Известно, что давление жидкости высотой h на дно сосуда определяется формулой P=gh, где  – плотность жидкости, а g – ускорение свободного падения. Эта формула справедлива, если =const. Для жидкостей это условие хорошо выполняется, т.к. жидкость мало сжимаема. С другой стороны, для воздуха это условие нарушается, т.к. с ростом высоты  уменьшается.

Выделим на некоторой высоте h над поверхностью моря объем газа высотой dh и сечением S (рис. 8.6). Тогда давление воздуха на нижнее основание выделенного цилиндра будет

Рис. 8.6.

,

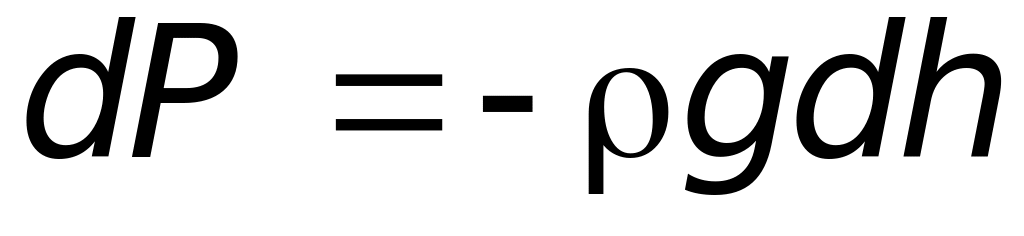(8.20)

где  – плотность воздуха на высоте h, а знак «минус» указывает, что с ростом высоты, давление атмосферы падает.

Найдём плотность воздуха  из уравнения Менделеева–Клапейрона

и подставим в (8.20). После разделения переменных получим:

.

Интегрируя последнее выражение в пределах от h₀ до h, получаем

,

(8.21)

где P и P₀ – давление атмосферы на высоте соответственно h и h₀.

Последняя формула выражает зависимость давления атмосферы от высоты над уровнем моря и называется барометрической формулой.

Если в выражении (8.21) положить h₀=0 (т.е. высоту отсчитывать от уровня моря), то барометрическая формула примет вид

,

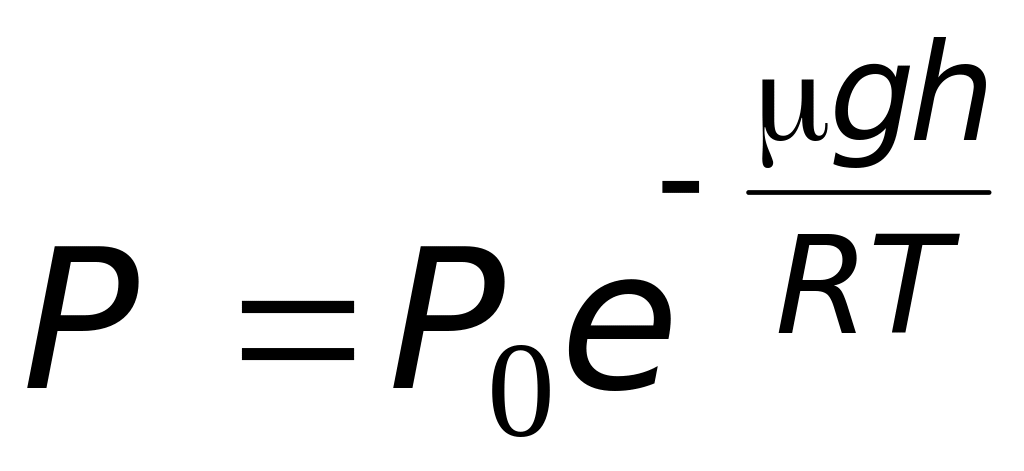(8.22)

Рис. 8.7.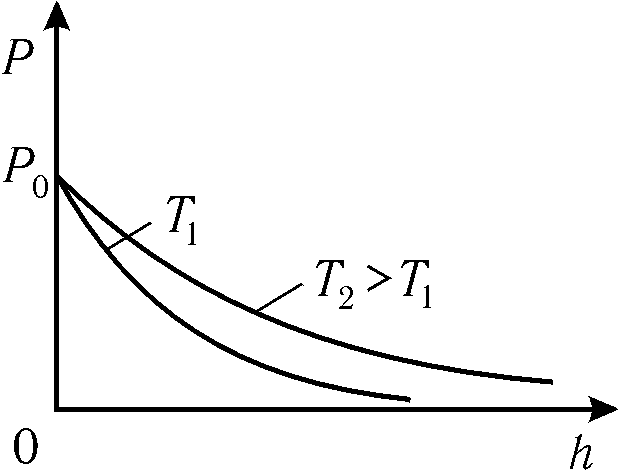

Следует отметить, что несмотря на значительное число упрощений, формула (8.22) достаточно хорошо описывает изменения атмосферного давления с высотой и применяется при определении высоты полета.

Нетрудно видеть, что при возрастании температуры зависимость P(h) будет более пологой (рис. 8.7), что может приводить к рассеиванию атмосферы на больших высотах – покиданию более быстрыми молекулами сферы притяжения данной планеты. Дальнейший анализ (8.22) позволяет также сделать ряд важных для астрономии выводов (отсутствие атмосферы на Луне вследствие малости g и т.д.).

4. Распределение Больцмана

Выразим давление газа на высотах h и h₀ через соответствующее число молекул в единице объема n и n₀:

.	(8.23)
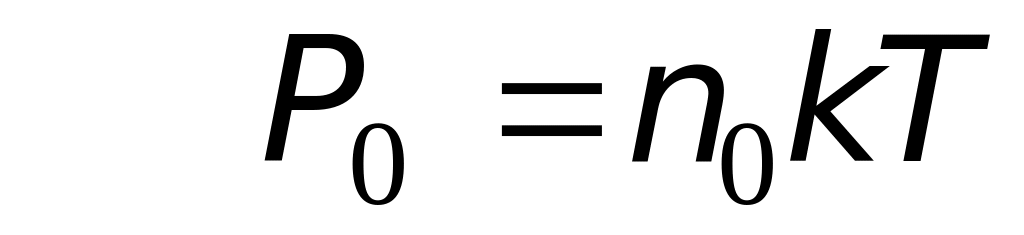.	(8.24)

Показатель степени в (8.21) преобразуем следующим образом:

(8.25)

где W_p= mgh–mgh₀ – изменение потенциальной энергии молекулы.

Температуру T на разных высотах по-прежнему будем считать постоянной.

Подставив (8.23) – (8.25) в формулу (8.21), получим

,

(8.26)

Это и есть распределение Больцмана для частиц, находящихся в потенциальном поле. Хотя эта формула была выведена нами для частного случая распределения молекул в поле тяжести Земли, она имеет универсальный характер – описывает распределение частиц по энергиям в любом потенциальном поле (например, зарядов в электростатическом поле).

Если потенциальную энергию частицы отсчитывать от нуля, то

,

(8.27)

Рис. 8.8.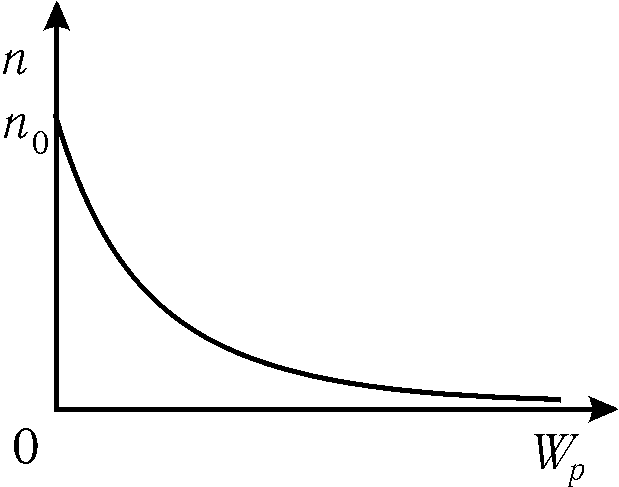

График распределения Больцмана (8.27) показан на рис. 8.8. Видно, что с ростом потенциальной энергии частиц их концентрация убывает. Таким образом, в распределении Больцмана проявляется принцип минимума энергии, который гласит, что любая физическая система стремится занять состояние с наименьшей потенциальной энергией.

В заключение отметим, что распределение Больцмана (8.27) можно обобщить, заменив потенциальную энергию полной энергией:

,

(8.28)