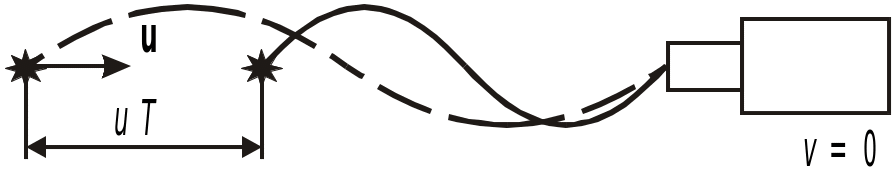4. Эффект Доплера в акустике

Эффект Доплера состоит в изменении частоты звуковых колебаний при движении источника или приемника относительно среды, в которой распространяются звуковые волны.

Обозначим: c — скорость звука в данной среде; u и v — скорость соответственно источника и приемника относительно среды. Различные частные случаи движения источника и приемника приведены в табл. 23.2.

Сделаем необходимые комментарии.

В случае 2 приемник движется навстречу источнику; скорость звука относительно приемника становится c+v. Формула (23.2) получается из (23.1) заменой в числителе с  с+v.

В случае 3 источник движется навстречу приемнику. Пока волна проходит по направлению к приемнику расстояние, равное длине волны ₀, источник успевает сместиться на расстояние uT, где T — период колебаний. Источник как бы сжимает волну в направлении своего движения и ее длина будет .

Таблица 23.2

№№	Движение источника или приёмника	Частота
1			(23.1)
2			(23.2)
			(23.2а)
3			(23.3)
			(23.3а)
4			(23.4)

Формула (23.3) получается из (23.1) заменой в знаменателе:

.

В формуле (23.4) (общий случай) верхний знак берется в случае сближения приемника и источника, а нижний — в случае удаления.

Эффект Доплера используется для определения скорости различных движущихся тел, начиная от астрономических объектов (звезд и галактик) и заканчивая судами и автотранспортом.

Лекція 11.

Молекулярная физика – это раздел физической науки, исследующий физические свойства и агрегатные состояния физических тел в зависимости от их молекулярного строения, характера теплового движения молекул и сил взаимодействия между ними.

Молекулярная физика основана на опытно установленных положениях.

1. Все физические тела состоят из отдельных частиц – молекул или атомов, между которыми имеются пустоты.

2. Частицы находятся в состоянии непрерывного хаотического (теплового) движения, интенсивность которого возрастает с температурой.

3. Между частицами (молекулами) действуют силы межмолекулярного взаимодействия, которые сложным образом зависят от вида частиц и расстояний между ними.

Для теоретического исследования указанного круга вопросов в молекулярной физике используются два взаимно дополняющих метода статистический и термодинамический. Охарактеризуем эти методы.

Состояние системы из небольшого числа частиц можно в принципе описать, используя динамический подход. Для этого, зная начальные координаты и импульсы частиц, необходимо решить уравнения динамики для каждой из них. При составлении таких уравнений необходимо знать конкретный характер взаимодействия между частицами. Если число частиц составляет N, то в общем случае необходимо решить 6N уравнений. В результате можно установить значения координат и импульсов всех частиц в любой момент времени.

Физические тела, исследуемые в молекулярной физике, представляют собой системы с очень большим числом частиц (например, при нормальных условиях в 1 см³ газа находится 10¹⁹ молекул). Для таких систем динамический подход совершенно неприменим, поскольку невозможно ни решить такое число уравнений, ни получить информацию о начальных значениях координат и скоростей всех молекул. Однако именно большое число частиц в макроскопических телах приводит появлению новых статистических закономерностей в поведении таких тел.

Кроме указанных основных положений молекулярной физики, в статистическом методе должны быть выполнены следующие положения.

1. Все молекулы движутся в соответствии с законами Ньютона, обладая в определенный момент времени определенными значениями координат и импульсов.

2. При взаимодействии молекул выполняются законы сохранения импульса, момента импульса и энергии.

3. Выполняется принцип различимости молекул, т.е. можно проследить за движением отдельно взятой молекулы (траекторией, импульсом и т.д.).

В статистическом методе анализ теплового движения частиц системы проводится методами математической теории вероятностей, с помощью которых рассчитываются средние характеристики движения частиц (средние скорости, энергии и т.д.), а затем находится связь между средними характеристиками движения частиц и макроскопическими свойствами системы в целом (температура, давление и т.д.).

Термодинамический метод состоит в изучении свойств систем взаимодействующих тел исследованием превращений энергии в них. В основе термодинамики лежат два установленных экспериментально принципа – законы термодинамики (см. §  9.2 и 9.8). Использование этих общих принципов позволяет отказаться от рассмотрения молекулярного строения конкретных тел, поэтому выводы термодинамики характеризуются чрезвычайно большой общностью. Однако термодинамический метод не дает сведений о механизме протекания конкретных физических процессов, что является его слабостью.

Статистический метод исследования принципиально глубже, чем термодинамический, поскольку позволяет получать информацию не только о конечных результатах того или иного процесса, но и о путях и стадиях его протекания. Однако применение статистического метода затруднено тем, что в статистическую модель должны вкладываться закономерности межмолекулярных взаимодействий, которые чрезвычайно сложны и недостаточно изучены.