3. Энергетические характеристики волновых процессов

Найдем вначале плотность энергии упругой волны. Выделим в среде элемент объема dV с массой dm=dV, где  — плотность среды. Бесконечно малую массу dm можно рассматривать как материальную точку, которая совершает гармонические колебания, полная энергия которых (см. §  21.6)

.

Отсюда плотность энергии упругой волны

.

(22.6)

Потоком энергии R называется количество энергии, проходящей через поверхность S за единицу времени: .

Рис. 22.2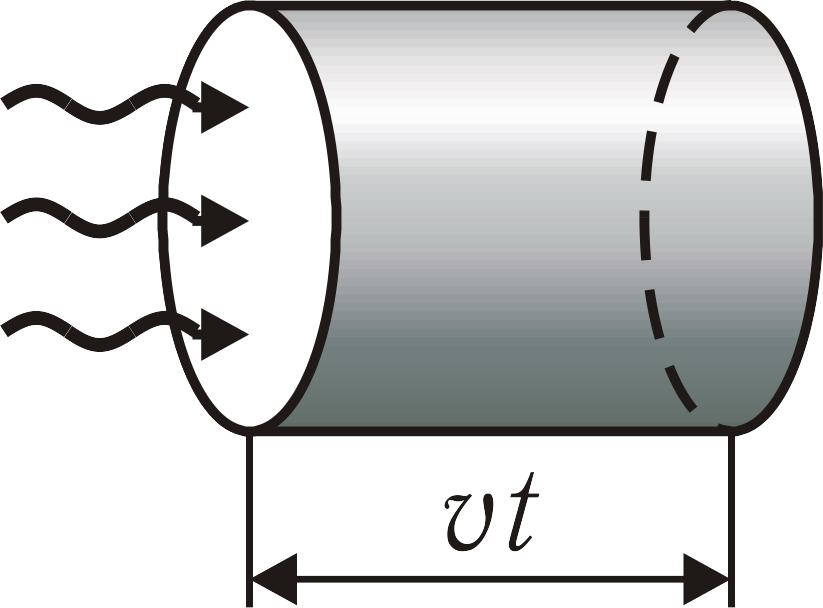

Для нахождения потока энергии подсчитаем количество энергии, которое переносится через площадку S, ориентированную перпендикулярно к лучу (рис. 22.2), за время t. Очевидно, что эта энергия сосредоточена в объеме цилиндра с высотой vt и сечением S:

,

.

(22.7)

Плотностью потока энергии называется количество энергии, переносимое волной через единичную площадку за единицу времени:

.

(22.8)

Для механических волн плотность потока энергии найдем, подставив (22.7) в (22.8):

.

(22.9)

Интенсивность волны I численно равна плотности потока энергии. Таким образом, интенсивность механической волны

.

(22.10)

Акустика

1. Объективные и субъективные характеристики звука

Звуковыми волнами называют упругие волны с частотами от 16 до 20000 Гц, воспринимаемые органами слуха человека.

Звуковые волны в жидких и газообразных телах являются продольными. В твердых телах могут распространяться как продольные, так и поперечные звуковые волны.

Упругие волны с частотой   16 Гц называют инфразвуком, а с частотой   2000 Гц — ультразвуком.

Благодаря упругим связям между частицами среды, колебания какой-нибудь частицы передаются соседней. Скорость передачи колебаний в упругой среде представляет собой скорость звука. Скорость звука в сухом воздухе при t = 0 °C v=331,6 м/с. С повышением температуры скорость звука в воздухе возрастает:

.

При распространении звуковых волн частицы среды совершают колебательные движения с определенной скоростью. Если эти колебания гармонические, то максимальная колебательная скорость

,

а эффективная колебательная скорость

.

Звуковые ощущения принято характеризовать громкостью, высотой и тембром. Эти характеристики являются субъективными. Соответствующие объективные характеристики даны в табл. 23.1.

Таблица 23.1

№№	Характеристики
	субъективные	объективные
1	Громкость звука	Интенсивность (сила) звука
2	Высота	Частота
3	Тембр	Форма звуковых колебаний

Интенсивность звуковой волны, как следует из формулы (22.10), пропорциональна квадрату амплитуды и частоты колебаний. Диапазон слышимости человека: 10^-6...10⁶ мкВт/м².

Физиологическая особенность восприятия звука человеком состоит в том, что если интенсивность звуковых волн возрастает в геометрической прогрессии, то громкость звука — в арифметической, т.е. приближенно справедлив закон: громкость звука, ощущаемая ухом, пропорциональна логарифму интенсивности звуковой волны.

Для сравнения интенсивности звука различной громкости пользуются единицей уровня звука — бел. Если интенсивность одного звука в 10 раз больше другого, то его громкость на 1 бел выше. Громкость звука связана с его интенсивностью законом Вебера-Фехнера:

,

где I₀ = 10^-12 Вт/м² — порог слышимости.

Высота звука, воспринимаемая человеком, определяется частотой звуковой волны. Звуки разной частоты воспринимаются человеком по-разному (рис. 23.1). На рис. 23.1 кривая 1 ограничивает область восприятия звуковых колебаний любого типа, кривая 2 — музыкальных звуков, кривая 3 — речи. Лучше всего воспринимаются звуковые волны частотой в несколько тысяч Герц.

Тембр звука определяется формой звукового сигнала или (что то же) числом одновременно звучащих музыкальных гармоник (тонов) — рис. 23.2. На этом рисунке а — музыкальная гармоника, б — созвучие (музыкальный звук) — наложение нескольких гармоник; в — шум — нерегулярное колебание, возникающее в результате сложения большого числа колебаний с близкими амплитудами, но различными частотами, г — взрыв.

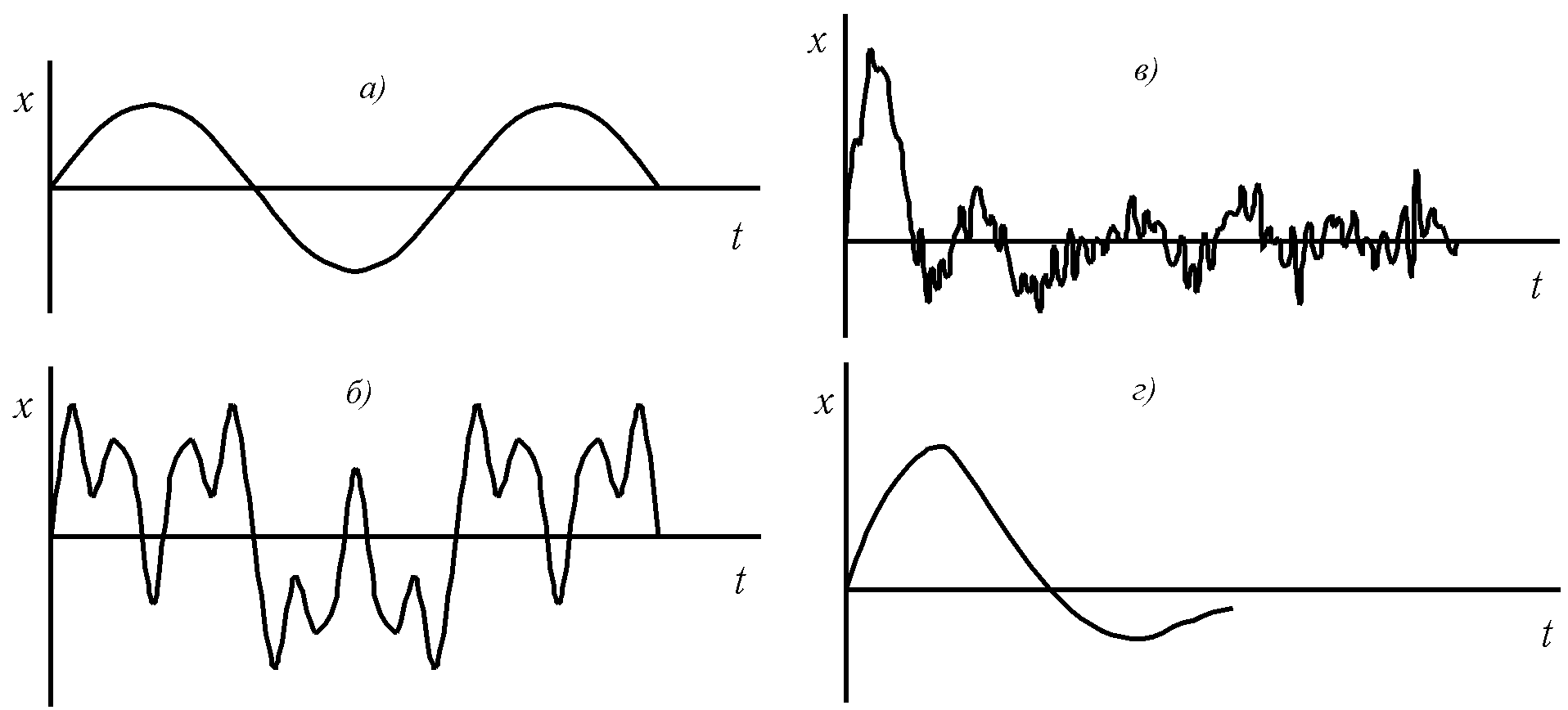
Р ис. 23.2

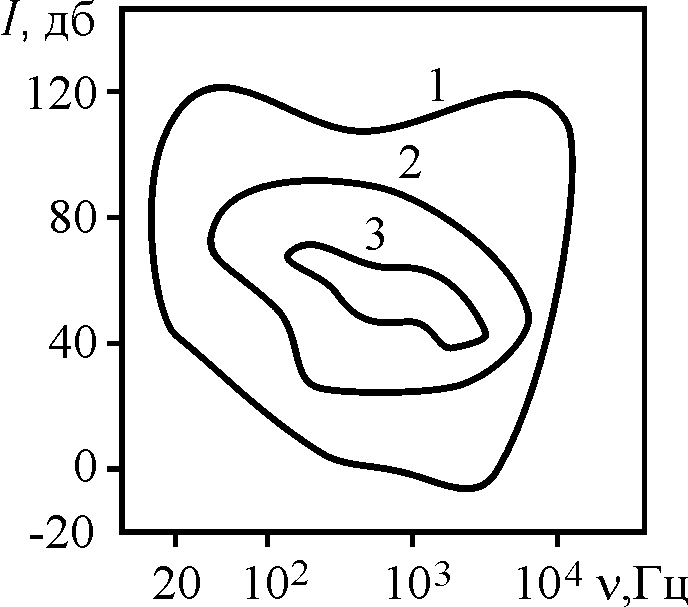
Рис. 23.1

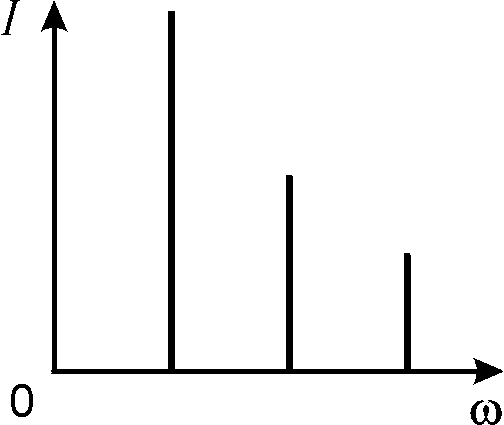
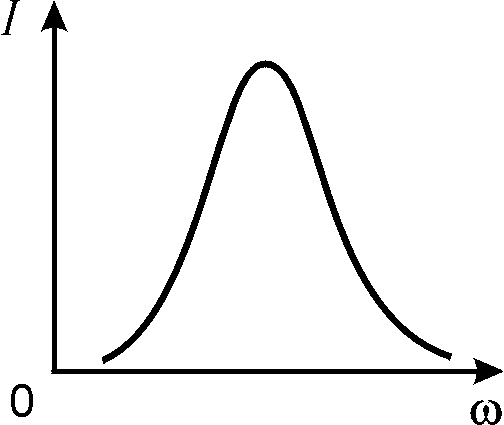
Частотный состав звука определяют с помощью его спектра. Спектр звука представляют обычно на координатной плоскости, где по оси абсцисс откладывается частота , а по оси ординат — амплитуда A соответствующей гармоники. Чистые тона, звуки с периодической формой волны, а также звуки, полученные при сложении нескольких волн, обладают линейчатым спектром (рис. 23.3). Акустические шумы, одиночные импульсы, затухающие звуки имеют сплошной спектр (рис. 23.4).

Рис. 23.3	Рис. 23.4