Лекція 7.

1.Общая характеристика колебательных процессов

Колебаниями называются движения или процессы, обладающие той или иной степенью повторяемости во времени.

В технике устройства, использующие колебательные процессы, могут выполнять определенные функциональные обязанности (маятник, колебательный контур, генератор колебаний и др.), а также могут возникать как неизбежное проявление физических свойств (вибрация машин и механизмов, неустойчивости и колебательные потоки при движении тел в жидкостях и газах и т.п.).

По мере изучения колебаний различной физической природы возникло убеждение о возможности единого подхода к ним, основанного на рассмотрении наиболее общих свойств и закономерностей колебательных процессов.

Рис. 21.1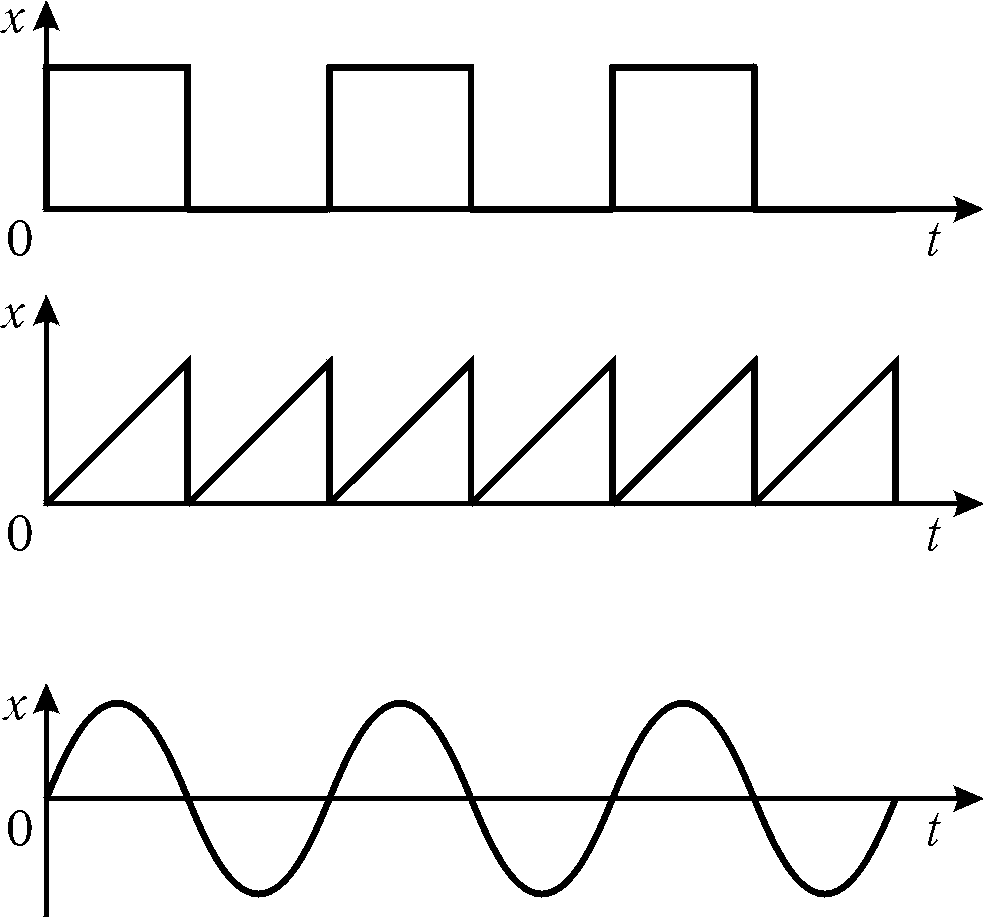

Колебания называются периодическими, если система через определенные равные промежутки времени, называемые периодом колебаний, проходит через одни и те же состояния. Такие колебания описываются периодическими функциями от времени

,

где x(t) — смещение от положения равновесия в момент времени t; T — период колебаний.

Примером периодических колебаний служат прямоугольные, пилообразные и гармонические колебания (рис. 21.1). Особенно важную роль в физике играют гармонические колебания, в которых зависимость смещения от времени определяется гармоническим законом

(21.1)

или

.

(21.2)

Здесь A — амплитуда колебаний, т.е. максимальное по модулю смещение от положения равновесия; ₀ — циклическая (или круговая) частота колебаний, равная числу полных колебаний, совершаемых за время 2 секунд. Удобно также характеризовать периодические колебания линейной частотой , которая равна числу полных колебаний, совершаемых за 1 с. Единица линейной частоты одни герц (Гц) — частота такого колебательного движения, в котором за 1 с совершается одно полное колебание.

В формулах (21.1) и (21.2) аргумент тригонометрической функции представляет собой фазу, которая показывает, какая часть колебания выполнена к данному моменту времени, если полному колебанию сопоставить значение 2. Обычно выделяют текущую фазу , значение которой изменяется со временем, и начальную фазу , определяющую смещение в начальный момент времени (t=0).

Гармонические колебания (21.1) и (21.2) удобно также представлять в комплексной форме:

.

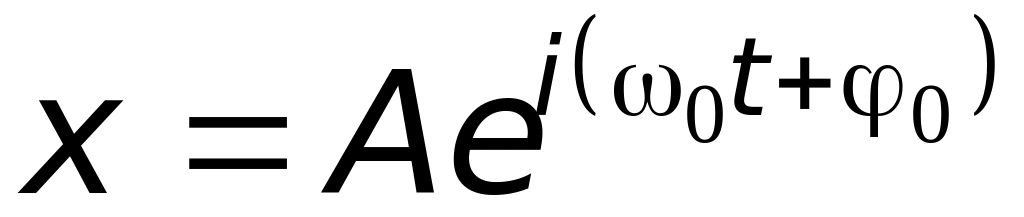(21.3)

Следует при этом помнить, что физический смысл имеет действительная или мнимая часть (21.3).

2. Дифференциальное уравнение гармонических колебаний

Исходя из (21.1), можно получить выражения для скорости v и ускорения a в гармоническом движении:

;	(21.4)
.	(21.5)

Используя комплексную форму гармонического колебания (21.3), можно получить эквивалентные выражения для скорости и ускорения:

;	(21.4а)
.	(21.5а)

Если воспользоваться формулой Эйлера (см. математическую справку) и взять действительную часть выражений (21.4а) и (21.5а), то получим (21.4) и (21.5).

Рис. 21.2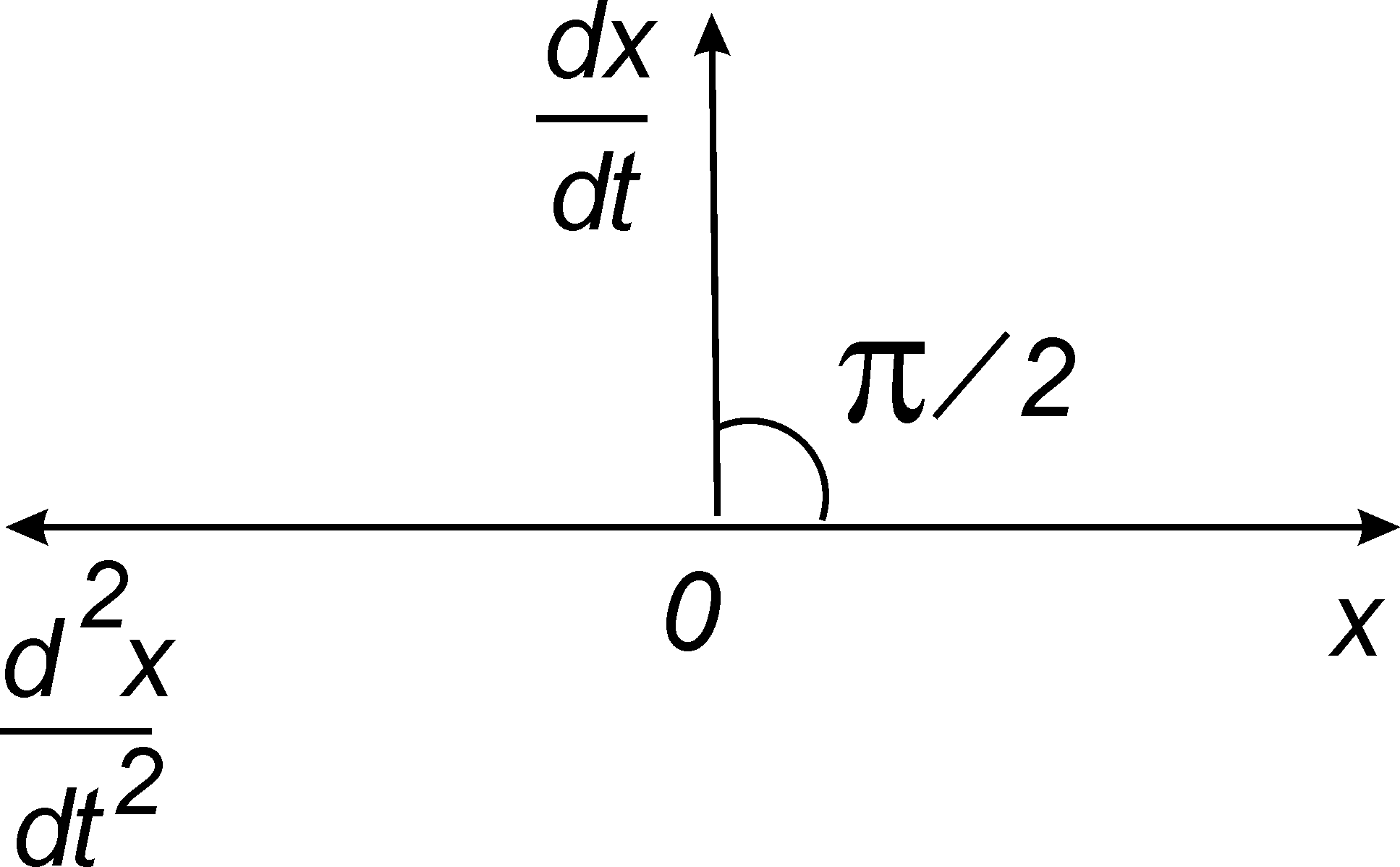

Если начало отсчета времени выбрать так, чтобы , то

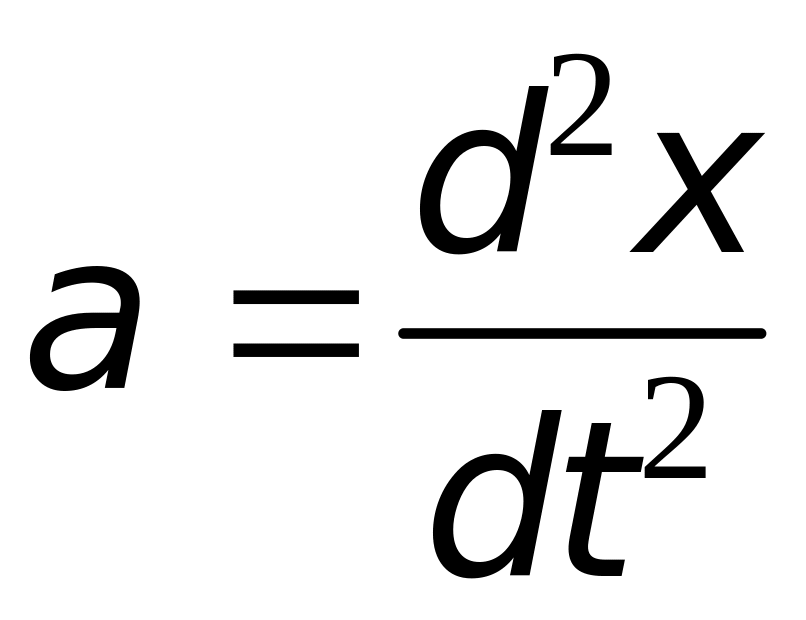. На комплексной плоскости числа расположатся на действительной оси, а число — на мнимой (рис. 21.2). Видно, что разность фаз между скоростью и смещением x равна /2. Ускорение и смещение x колеблются в противофазе.

Из (21.5) следует уравнение гармонических колебаний в дифференциальной форме:

.

(21.6)