Алгебра.
Вычислить
и
Вычислить
тремя способами (по определению,
разложениями по первому столбцу,
приведением к треугольному виду).Найти ранг матрицы
.Вычислить
двумя
способами (методом Гаусса, с помощью
алгебраических дополнений).Решить систему методом Гаусса
.Решите систему по правилу Крамера
.
;
Найти:
Исследовать систему на совместимость (с помощью теоремы Кронекера-Капелли)
Найти фундаментальную систему решений линейной системы уравнений:
Проверить, являются ли вектора
,
,
,
линейно зависимыми или линейно
независимыми.Найти собственные числа, собственные векторы линейного оператора А, заданного в стандартном базисе матрицей
.
Дифференциальные уравнения
Решить уравнение
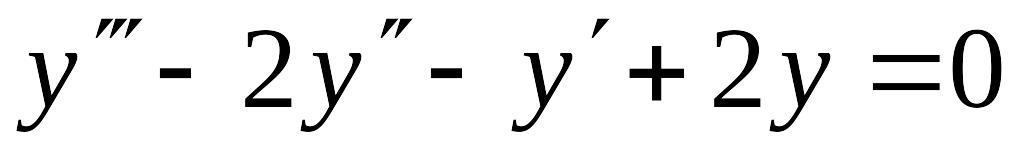
Решить уравнение
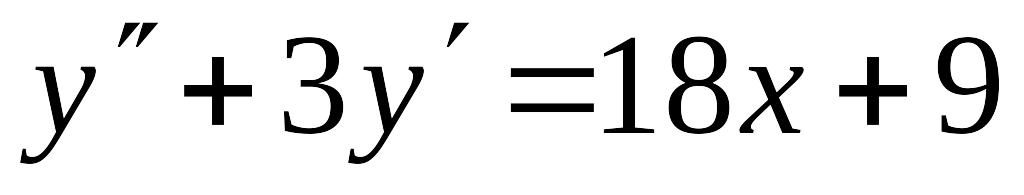
Решить уравнение
Найти решение уравнения
,
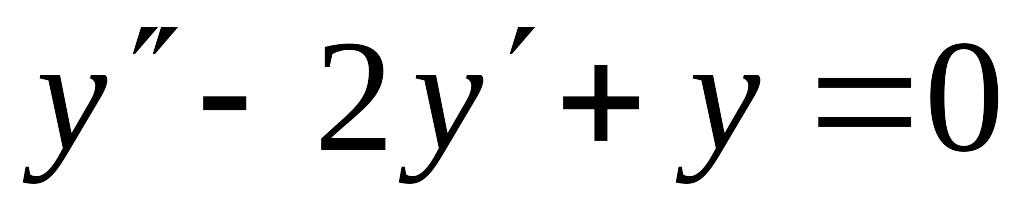удовлетворяющее начальным условиям
Решить систему уравнений
Решить систему уравнений
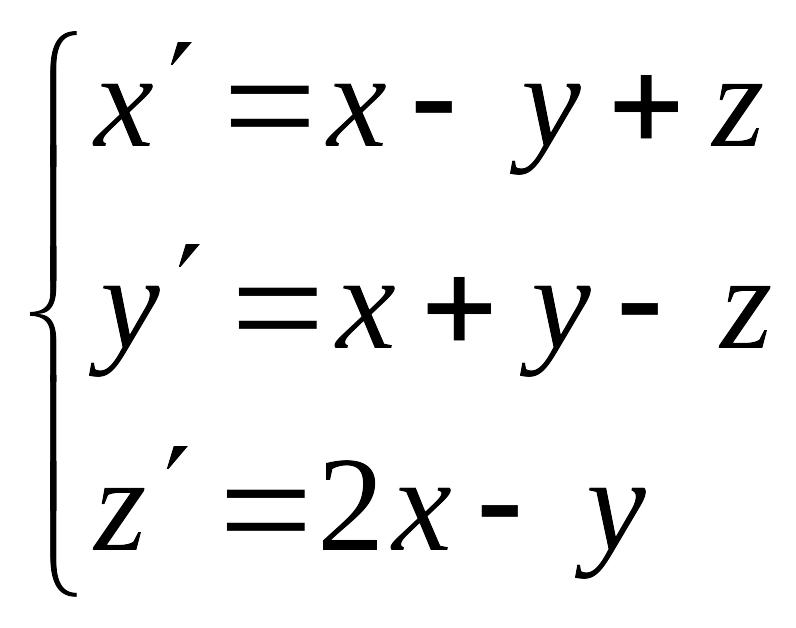
Решить систему уравнений
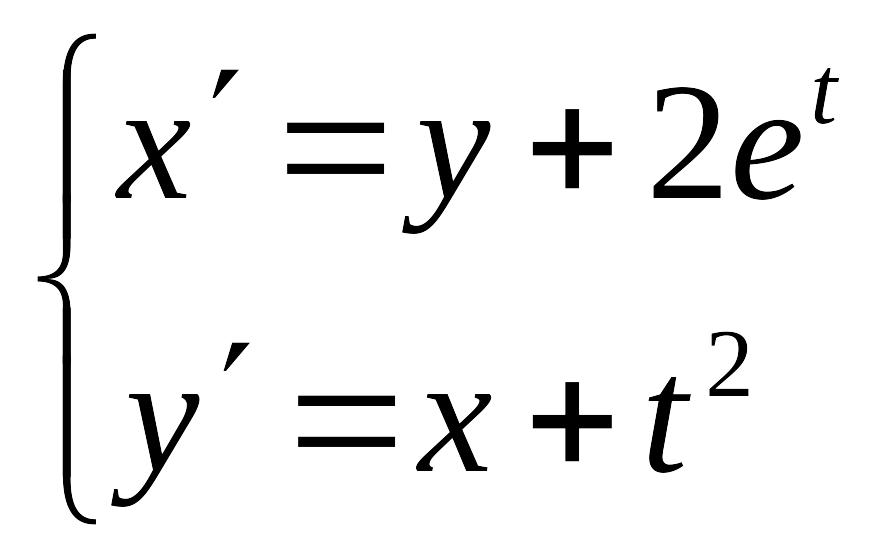
Решить линейное дифференциальное уравнение с постоянными коэффициентами
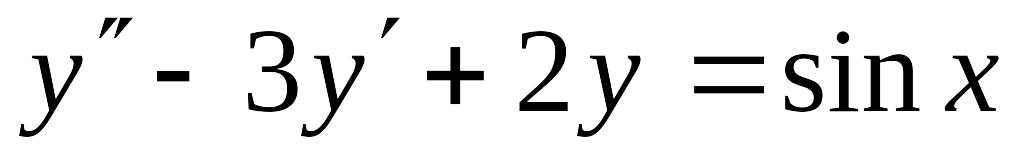
Решить линейное дифференциальное уравнение с постоянными коэффициентами
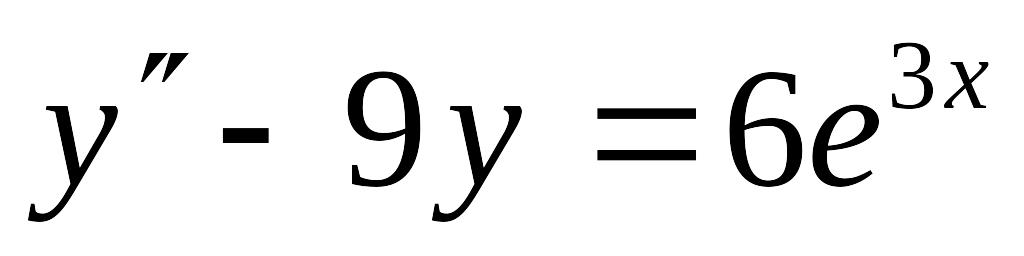
Решить линейное дифференциальное уравнение с постоянными коэффициентами
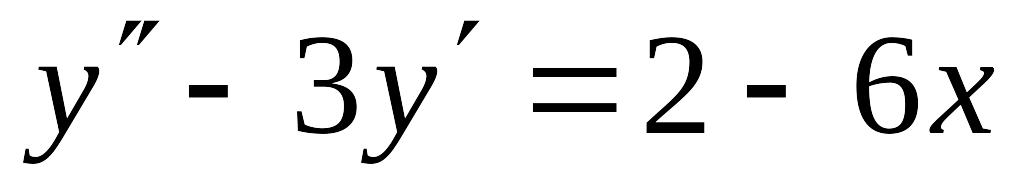
Решить линейное дифференциальное уравнение с постоянными коэффициентами
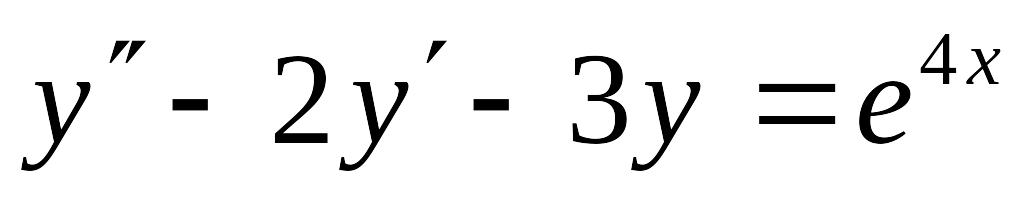
Решить дифференциальное уравнение с разделяющимися переменными
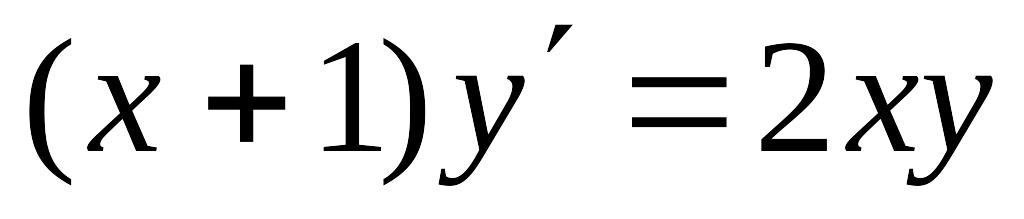.Решить уравнение
.Решить уравнение методом вариации произвольных постоянных
.Решить уравнение методом вариации произвольных постоянных
.Решить систему уравнений
.Решить систему уравнений
.Решить систему уравнений
Решить систему уравнений
Решить систему уравнений методом вариации произвольных постоянных
.Решить систему уравнений методом вариации произвольных постоянных
.Решить равнение
.Решить уравнение Бернулли
.Решить уравнение
.Найдите решение уравнения
при
.Найдите решение линейного уравнения
,
удовлетворяющее условию
.Решите систему уравнений
.Решите систему уравнений .
Уравнения математической физики
Решить задачу:
Решить задачу:
Решить задачу:
Решить задачу:
Решить задачу:
Решить задачу:
Решить задачу:
Решить задачу:
Решить задачу:
Привести уравнение к каноническому виду:
.Привести уравнение к каноническому виду:
.Привести уравнение к каноническому виду:
.Решить уравнение
.Решить уравнение
;
при
Найти общее решение уравнения
Теория вероятностей и математическая статистика
В первом ящике 3 белых и 5 черных шаров; во втором ящике 4 белых и 6 черных шаров. Из каждого ящика вынули по шару. Какова вероятность того, что шары разного цвета?
Какова вероятность, что дни рождения 4-х человек из случайно выбранных 6 людей приходятся на 2 определенных месяца года?
Случайная величина
имеет ряд распределения
|
-4 |
m |
2 |
3 |
5 |
|
0,2 |
|
|
0,25 |
|
Найти
,
если известно, что
Плотность распределения величины имеет вид
Найти
значение параметра
,
а также вычислить
и
.
Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором – 10 белых и 10 черных шаров, в третьем – 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.
Точка взята наудачу внутри круга радиуса R. Найти вероятность того, что эта точка окажется от центра на расстоянии, большем
.В ящике 6 белых и 8 черных шаров. Из ящика вынули 2 шара (не возвращая вынутый шар в ящик). Найти вероятность того, что оба шара белые.
Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,6 для второго – 0,8, для третьего – 0,9. определить вероятность того, что в цель попадет хотя бы один стрелок.
Имеется пять урн. В 1-й, 2-й и 3-й урнах находится по 2 белых и 3 черных шара. В 4-й и 5-й урнах - по 1 белому и 1 черному шару. Случайно выбирается урна и из неё извлекается шар. Какова вероятность того, что выбрана 4-я или 5-я урна, если извлеченный шар оказался белым?
Устройство состоит из 8 независимо работающих элементов. Вероятности отказов каждого из элементов за время
одинаковы и равны
.
Найти вероятность отказа устройства,
если для этого достаточно, чтобы отказали
не менее 3 элементов.Производится стрельба до попадания по удаляющейся цели. Вероятность попадания первым выстрелом равна 0,8, а при каждом следующем выстреле она уменьшается на 0,1. У стрелка имеется боезапас 5 патронов. Найти распределение числа израсходованных патронов и его математическое ожидание.
Функция плотности распределения случайной величины имеет вид:
Определить
параметр
и
.
Вероятность появления события
в каждом из 8000 независимых опытов равна
.
Оценить вероятность того, что число
появлений события
будет более 1800 и менее 2200.Известно, что дискретная случайная величина Х принимает значения:
а также
,
.
Найти вероятности, соответствующие
указанным значениям Х.Группа студентов из 15 юношей и 10 девушек выбирает по жребию спортивную команду в составе 5 человек. Какова вероятность того, что в этой команде окажутся 3 юношей?
Из 50 вопросов, включенных в экзамен, студент подготовил 30. Какова вероятность того, что из предложенных ему трех вопросов он знает ответ на: а) три вопроса; б) два вопроса?
В урне находятся 15 одинаковых шаров, причем 10 из них одинакового цвета. Наудачу извлечены 3 шара. Найти вероятности следующих событий: а) два из них окрашены одинаково; б) хотя бы 2 окрашены одинаково.
Производится 3 независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Для случайного числа появления события А в 3 опытах составить таблицу распределения. Найти математическое ожидание и дисперсию.
В ящике имеются 9 шаров, 3 из которых белые, остальные черные. Случайным образом достаются 3 шара. Составить закон распределения для случайного числа белых шаров среди отобранных.
Случайная величина Х задана плотностью распределения вероятностей:
.
Найти: 1) функцию
распределения и построить ее график;
2) вероятность того, что случайная
величина Х примет значения из интервала
(0, π/2).Случайная величина задана функцией распределения вероятностей:
1)
Построить график интегральной функции,
2)
Найти плотность вероятности,
3) Найти
математическое ожидание и дисперсию.