Міністерство освіти і науки України

Державний університет ТеЛЕКОМУНІКАЦІЙ

КАФЕДРА ВИЩОЇ МАТЕМАТИКИ

ЗАТВЕРДЖУЮ

Завідуючий кафедрою

________________Барабаш О.В.

“ ____ “ _____________ 2014 року

Л Е К Ц І Я № 1.

МОДУЛЬ 1

Тема 1: „Лінійна алгебра”

Різновиди матриць. Визначники та їх властивості.

Дії з матрицями: множення на число, алгебраїчна сума, множення матриць, знаходження оберненої матриці та рангу матриці.

з навчальної дисципліни вища математика

напряму підготовки телекомунікації

освітньо-кваліфікаційного рівня бакалавр

Лекція розроблена

кандидатом фіз.-мат. наук, доцентом Онищенко В.В.

Обговорено на засіданні кафедри (ПМК)

Протокол № __________

“ ____ “ _____________ 2013 року

Київ - 2014

Навчальні цілі: Ознайомити студентів з предметом, структурою і характерними рисами вищої математики, з її значенням та специфікою організації навчального процесу, з різновидами матриць та визначників.

Виховні цілі: Обґрунтувати, що якісне вивчення вищої математики сприяє:

• розвитку логічного та аналітичного мислення, пам’яті;

• можливості самостійно вивчати сучасну науково-технічну літературу;

• вмінню коротко і зрозуміло висловлювати свої думки;

• акуратності і точності записів, уважності, дисциплінованості;

• вмінню конспектувати, красиво оформлювати записи робочих зошитів для практичних занять та індивідуальних робіт;

• набуттю навичок систематизації матеріалу, що вивчається.

Час: 1,5 години.

План проведення лекції та розрахунок часу

Введення.

Представитись та привітати зі вступом до ДУТ. 1 хвилина

Навчальні питання:

І. Вступ

1. Структура дисципліни і зв’язок з іншими навчальними дисциплінами 5хв.

2. Рекомендована література 2 хвилин

3. Специфіка організації навчального процесу і контролю 5 хвилин

ІІ.Основна частина

1. Різновиди матриць 15 хвилин

2. Визначники 15 хвилин

3. Властивості визначників 15 хвилин

4. Найпростіші дії з матрицями 15 хвилин

5. Ранг матриці та обернена матриця 15 хвилин

ІІІ. Заключення 2 хвилин

НАВЧАЛЬНО-МАТЕРІАЛЬНЕ ЗАБЕЗПЕЧЕННЯ

Бажано мати:

1. крейду і вологу губку;

Навчальні матеріали

I. Текст лекції іі.Основна частина

1. Різновиди матриць

Означення 1. Матрицею називають таблицю упорядкованих чи­сел або будь-яких інших об'єктів, розташованих в m рядках та п стовпцях.

Матриці позначають великими літерами, наприклад А, В, С... та круглими дужками.

Матриця, яка має m рядків та п стовпців, називається матри­цею розміру (перший множник завжди вказує кількість рядків). Така матриця має вигляд

.

Кожен елемент матриці А має два індекси: перший індекс і вказує номер рядка, в якому знаходиться цей елемент, другий індекс j вказує номер стовпця, який містить цей елемент. Так, елемент а₂₃ знаходиться на перетині другого рядка та третього стовпця матриці А.

Матриця розміру називається матрицєю-стовпцем або вектором-стовпцем. Матриця розміру називається матрицєю-рядком або вектором-рядком.

Наприклад, нехай задані матриці

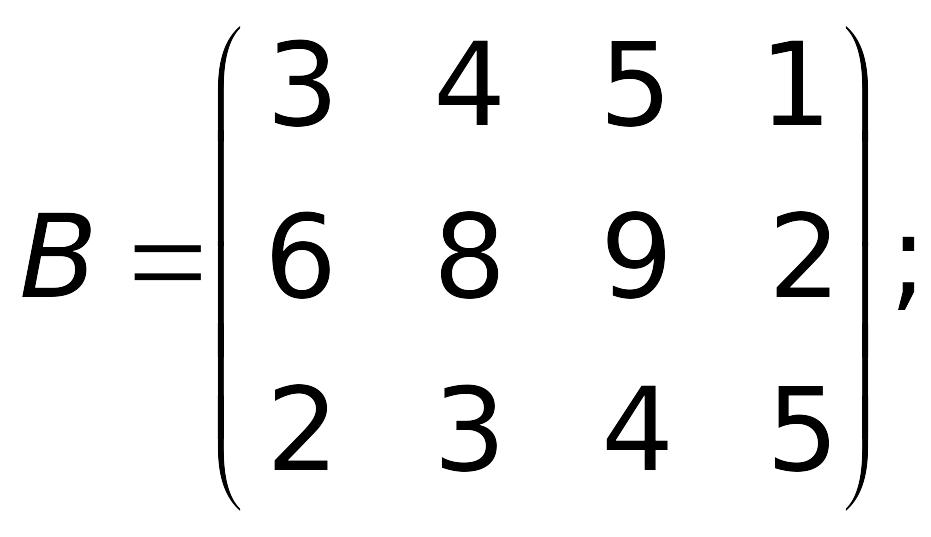
Матриця А має розмір , матриця В розміру , С – матриця-стовпець розміру , D – матриця-рядок .

Матрицю називають квадратною порядку n, якщо кількість її рядків однакова з кількістю стовпців і дорівнює n.

Наприклад, квадратна матриця А порядку n має вигляд

.

Множина елементів а₁₁, а₂₂, а₃₃, ..., а_nn квадратної матриці А порядку n утворюють головну діагональ матриці, а множина елементів утворює допоміжну (або него­ловну) діагональ матриці.

Квадратна матриця, у якій лише при і = j називається ді­агональною. Діагональна матриця з елементами називається одиничною матрицею і найчастіше позначається Е або І.

Наприклад, нехай задані матриці

.

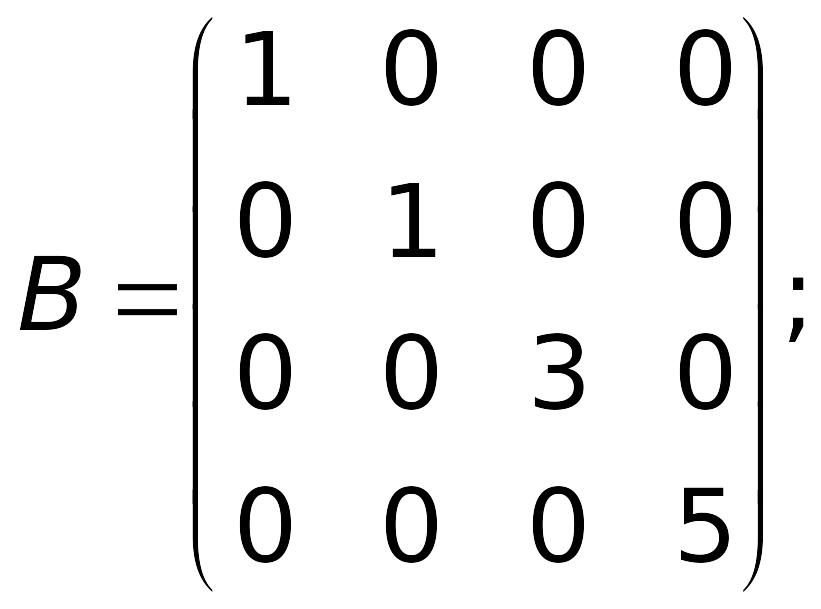
В – діагональна матриця 4-го порядку, Е – одинична матри­ця порядку 3, 0 – нульова квадратна матриця порядку 3.

Для скорочення матриці можна записати у вигляді коли розмір матриці А відомий, або

Матриці А та В називають рівними, якщо:

1. вони мають однаковий розмір;

2. їх відповідні елементи рівні, тобто 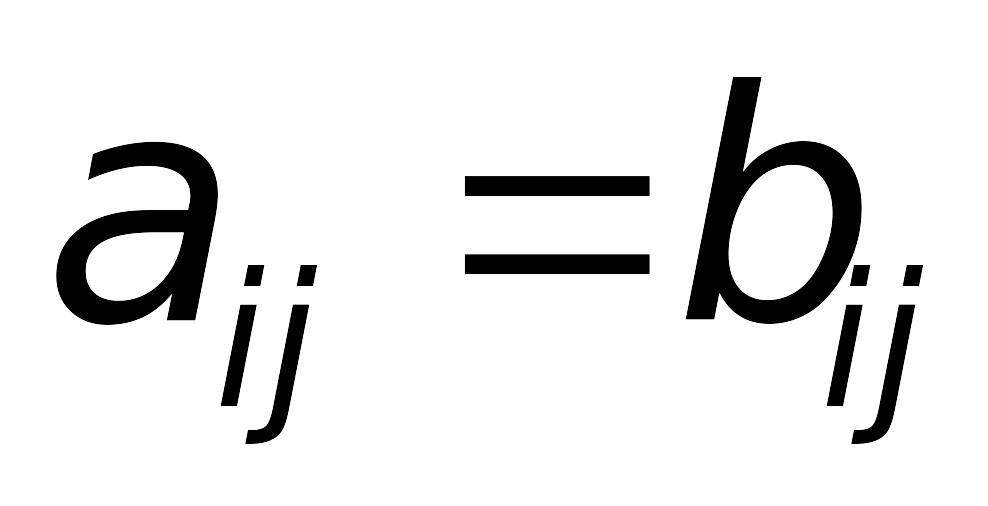для усіх і = 1, 2, ..., m: j = 1, 2 , ..., n.

Якщо в матриці А рядки записати стовпцями із збереженням їх порядку, то одержану матрицю називають транспонованою і позначають А^T, а вказана операція перетворення матриці А називається транспонуванням матриці А. Наприклад,

якщо тоді

Матриці широко використовуються в плануванні виробниц­тва та транспортних перевезень. Вони дозволяють розробляти різні варіанти плана, полегшують дослідження залежності між різними економічними показниками.