Лабораторная работа № 8 Тема: «Исследование счётчиков электрических импульсов»

Цель работы: научится исследовать суммирующие и вычитающие счётчики импульсов и строить временные диаграммы их работы

Краткая теория

Счётчиком называют функциональный узел, который осуществляет счёт поступивших на его вход импульсов, формирует результат счёта в заданном коде, при необходимости хранит его, а также производит деление частоты входного сигнала.

Простейшим счётчиком, считающим до двух, является триггер. Счётчики делятся на простые и реверсивные. Простые счётчики бывают суммирующие – их показания увеличиваются на 1 с приходом каждого следующего импульса, и вычитающие – их показания уменьшаются на 1. Реверсивные счётчики могут работать как суммирующие и как вычитающие.

Каждый счётчик характеризуется коэффициентом счёта К_сч, т.е. общим числом возможных состояний счётчика. По коэффициенту счёта счётчики делятся на: двоичные (бинарные), у которых К_сч = 2ⁿ , где n – количество триггеров; двоично-десятичные (декадные), К_сч = 10ⁿ; с переменным коэффициентом счёта К_сч 2ⁿ.

По способу организации внутренних связей счётчики бывают с последовательным переносом и с параллельным переносом (кольцевые, Джонсона).

1 Суммирующий счётчик

Счётчики с последовательным переносом строят на основе Т-триггеров с двухступенчатой структурой. Рассмотрим простейший счётчик, состоящий из цепочки 4-х триггеров (рисунок 8.1).

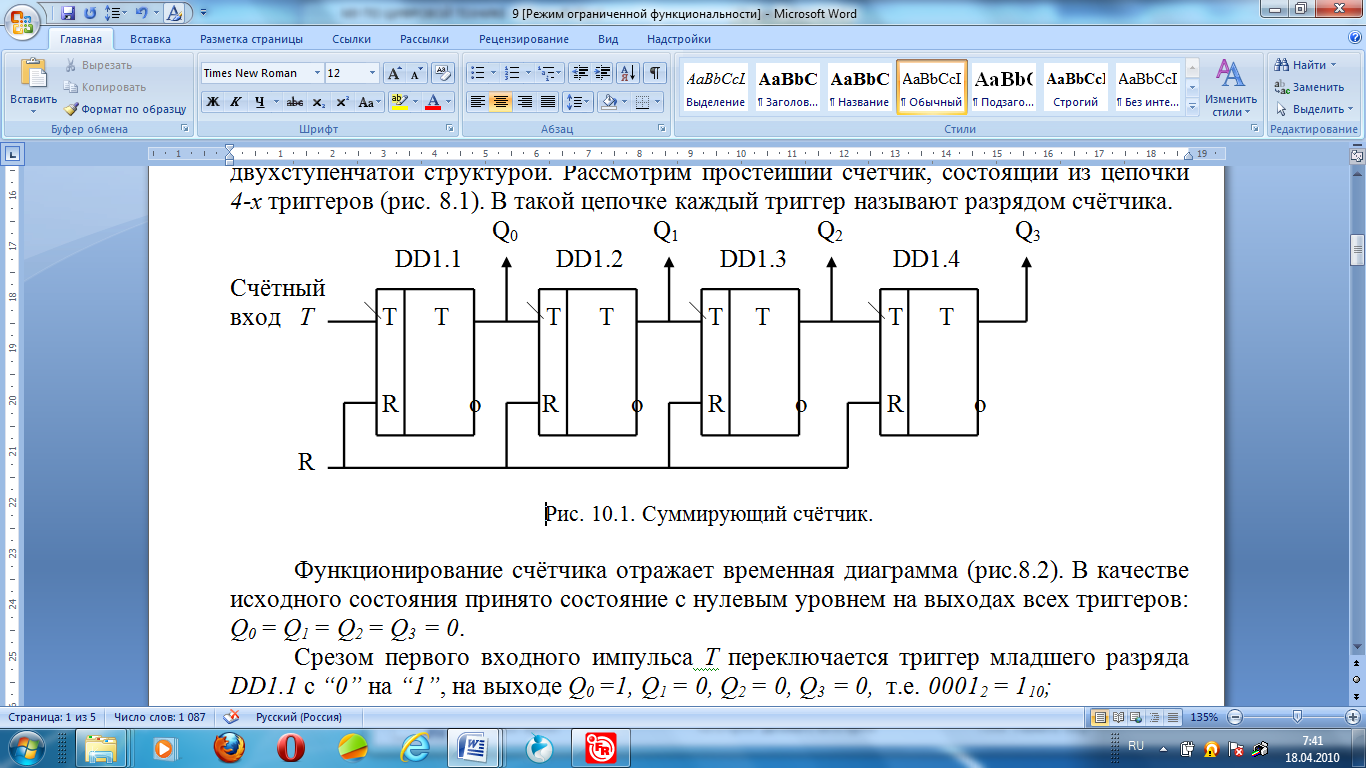
Рисунок 8.1 - Суммирующий счетчик

В такой цепочке каждый триггер называют разрядом счётчика.

Функционирование счётчика отражает временная диаграмма (рисунок 8.2).

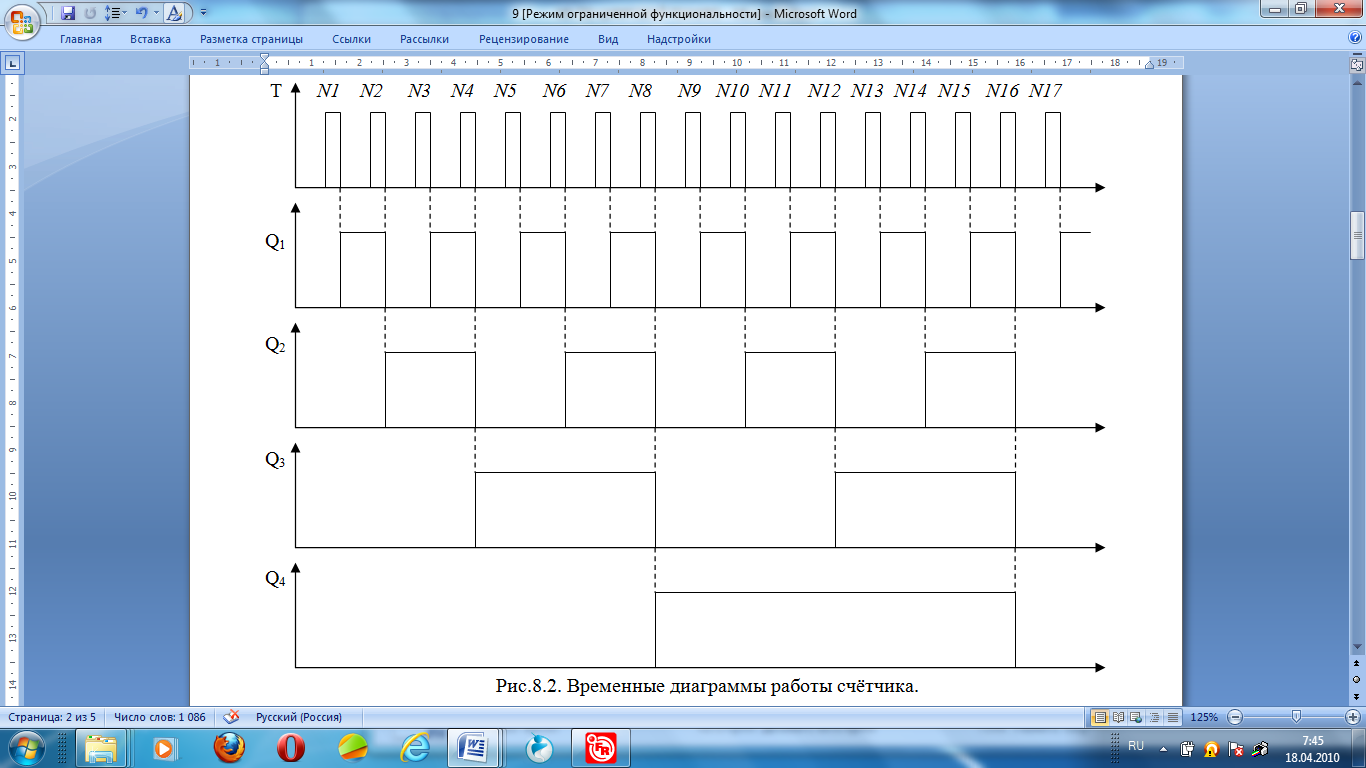
Рисунок 8.2 - Временная диаграмма работы суммирующего счётчика

В качестве исходного состояния принято состояние с нулевым уровнем на выходах всех триггеров: Q₀ = Q₁ = Q₂ = Q₃ = 0.

Срезом первого входного импульса Т переключается триггер младшего разряда DD1.1 c «0» на «1», на выходе Q₀ =1, Q₁ = 0, Q₂ = 0, Q₃ = 0, т.е. 0001₂ = 1₁₀;

Срезом второго импульса Т первый триггер переключится на “0”, а второй перепишет единицу из первого, на выходе Q₀ = 0, Q₁ = 1, Q₂ = 0, Q₃ = 0, т.е. 0010₂ = 2₁₀.

По четвёртому импульсу на выходе Q₀ = 0, Q₁ = 0, Q₂ = 1, Q₃ = 0, т.е. 0100₂ = 4₁₀. По восьмому импульсу на выходе Q₀ = 0, Q₁ = 0, Q₂ = 0, Q₃ = 1, т.е. 1000₂ = 8₁₀, и т.д. По пятнадцатому импульсу на выходе Q₀ = Q₁ = Q₂ = Q₃ = 1, т.е. 1111₂ = 15₁₀; по срезу 16-го импульса на счётчике Q₀ = Q₁ = Q₂ = Q₃ = 0, т.е. счётчик автоматически сбрасывается. При дальнейшем поступлении импульсов начинается новый цикл счёта.

Из схемы счётчика (рисунок 8.1) и временных диаграмм (рисунок 8.2) можно сделать выводы:

1. Данный счётчик осуществляет счёт импульсов от 0 до 15, т.е. К_сч = 2⁴ = 16, т.к. в данном счётчике 4 разряда (триггера);

2. Максимальное число N которое может быть записано в счётчике N = 2ⁿ -1 = 2⁴ - 1 = = 15;

3. Состояние разрядов (триггеров) представляет собой запись числа поступивших импульсов в двоичном коде (т.е. 0 или 1);

4. Состояния триггера отвечают в двоичном коде порядковому номеру воздействующего импульса, например, после 11 входящего импульса на выходе Q₀ = 1, Q₁ = 1, Q₂ = 0, Q₃ = 1, т.е. 1011₂ = 11₁₀. Записанное в счётчик число можно определить как:

M = 1·2³ + 0·2² + 1·2¹ + 1·2⁰ = 8+0+2+1=11.

5. Результат счёта снимается в виде двоичного кода с выходов всех разрядов одновременно.

6. Каждый входной импульс увеличивает число, записанное в счетчик на 1. Такой счётчик называют суммирующим.

7. По срезу 16 импульса счётчик автоматически сбрасывается и начинается новый цикл счёта.

8. Частота повторения выходного сигнала в n разряде в 2ⁿ раза меньше частоты повторения входных импульсов Т, т.е.

9. У счётчиков, работающих в режиме деления, используется выходной сигнал только последнего триггера.

Достоинства: простота схемы.

Недостатки:

1. Низкое быстродействие, т.к. триггеры в счётчике срабатывают последовательно один за другим.

2. Изменение состояния счётчика происходит с задержкой, вызванной переходными процессами на n-p – переходах транзисторов. Задержка нарастает с числом разрядов. У четырёхразрядных счётчиков задержка на четвёртом разряде в 4 раза больше задержки первого разряда.

Из-за такого накопления временных сдвигов в разрядах на выходах таких счётчиков могут появиться кратковременные ложные импульсы. Поэтому, несмотря на простоту, их применение ограничено цифровыми устройствами с небольшим числом разрядов.