
2 Численное решение обыкновенного дифференциального уравнения 1 порядка
Для оценки качества численного решения уравнения (2.1) используем аналитическое решение.
(2.1)
где τ - время,
X(τ) - воздействие,
Y(τ) - реакция оъекта.
2.1 Аналитическое решение уравнения (2.1)
Аналитическое решение уравнения (2.1) при начальных условиях =0 Y=Y0 и воздействии (2.2) имеет вид (2.3).
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
где
![]() .
.
Например, для n=4
![]() .
.
2.2 Численные решение уравнения (2.1)
Рассматривается явная разностная схема.
![]()
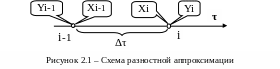 или
или
![]() (2.4)
(2.4)
где
![]()
Условие
абсолютной устойчивости:
![]() или
или
![]() .
.
Рассматривается аналитико-сеточная схема с постоянным воздействием на отрезке интегрирования.
![]() (2.6)
(2.6)
или
![]()
где
![]() ,
,
![]()
Условие
абсолютной устойчивости:
![]() выполняется всегда.
выполняется всегда.
Аналитическое и численное решения приведены в таблице 2.1.
Таблица 2.1 – Исходные данные
A= |
1 |
a0= |
0,5 |
C0= |
0,34 |
|
D1яс= |
0,800 |
k= |
1 |
a1= |
0,1 |
C1= |
0,16 |
|
D2яс= |
0,200 |
= |
0,2 |
a2= |
-0,06 |
C2= |
-0,03 |
|
D1ас= |
0,818731 |
Y0= |
0 |
a3= |
-0,002 |
C3= |
-0,01 |
|
D2ас= |
0,090635 |
|
|
a4= |
0,002 |
C4= |
0,002 |
|
Ymax= |
0,651157 |
|
|
|
|
|
|
|
Ymin= |
0 |
Таблица 2.2 - Расчет
i |
|
X |
Ya |
Yяс |
Yac |
яс |
ас |
яс |
ас |
1 |
0 |
0,5 |
0 |
0 |
0 |
0,0E+00 |
0,00E+00 |
0,0% |
0,00% |
2 |
0,2 |
0,5176 |
0,09235 |
0,1 |
0,09223 |
7,65E-03 |
-1,26E-04 |
1,2% |
-0,02% |
3 |
0,4 |
0,5303 |
0,1707 |
0,18352 |
0,17049 |
1,28E-02 |
-2,15E-04 |
2,0% |
-0,03% |
4 |
0,6 |
0,5382 |
0,2367 |
0,25288 |
0,23643 |
1,62E-02 |
-2,72E-04 |
2,5% |
-0,04% |
5 |
0,8 |
0,5414 |
0,29173 |
0,30995 |
0,29142 |
1,82E-02 |
-3,03E-04 |
2,8% |
-0,05% |
6 |
1 |
0,54 |
0,33692 |
0,35624 |
0,33661 |
1,93E-02 |
-3,11E-04 |
3,0% |
-0,05% |
7 |
1,2 |
0,5343 |
0,37326 |
0,39299 |
0,37296 |
1,97E-02 |
-3,00E-04 |
3,0% |
-0,05% |
8 |
1,4 |
0,5246 |
0,4016 |
0,42125 |
0,40133 |
1,97E-02 |
-2,74E-04 |
3,0% |
-0,04% |
9 |
1,6 |
0,5113 |
0,4227 |
0,44192 |
0,42247 |
1,92E-02 |
-2,35E-04 |
3,0% |
-0,04% |
10 |
1,8 |
0,4949 |
0,43727 |
0,4558 |
0,43709 |
1,85E-02 |
-1,86E-04 |
2,8% |
-0,03% |
11 |
2 |
0,476 |
0,44599 |
0,46363 |
0,44586 |
1,76E-02 |
-1,29E-04 |
2,7% |
-0,02% |
12 |
2,2 |
0,4552 |
0,4495 |
0,4661 |
0,44943 |
1,66E-02 |
-6,61E-05 |
2,5% |
-0,01% |
13 |
2,4 |
0,4331 |
0,44847 |
0,46391 |
0,44847 |
1,54E-02 |
4,66E-08 |
2,4% |
0,00% |
14 |
2,6 |
0,4106 |
0,44358 |
0,45775 |
0,44365 |
1,42E-02 |
6,79E-05 |
2,2% |
0,01% |
15 |
2,8 |
0,3886 |
0,43554 |
0,44833 |
0,43567 |
1,28E-02 |
1,36E-04 |
2,0% |
0,02% |
16 |
3 |
0,368 |
0,42507 |
0,43639 |
0,42527 |
1,13E-02 |
2,02E-04 |
1,7% |
0,03% |
17 |
3,2 |
0,3498 |
0,41298 |
0,42271 |
0,41324 |
9,73E-03 |
2,65E-04 |
1,5% |
0,04% |
18 |
3,4 |
0,3351 |
0,40008 |
0,40812 |
0,4004 |
8,04E-03 |
3,23E-04 |
1,2% |
0,05% |
19 |
3,6 |
0,325 |
0,38727 |
0,39351 |
0,38765 |
6,24E-03 |
3,74E-04 |
1,0% |
0,06% |
20 |
3,8 |
0,3209 |
0,3755 |
0,37981 |
0,37592 |
4,31E-03 |
4,18E-04 |
0,7% |
0,06% |
21 |
4 |
0,324 |
0,36577 |
0,36803 |
0,36623 |
2,25E-03 |
4,53E-04 |
0,3% |
0,07% |
22 |
4,2 |
0,3358 |
0,35916 |
0,35922 |
0,35964 |
5,99E-05 |
4,77E-04 |
0,0% |
0,07% |
23 |
4,4 |
0,3577 |
0,3568 |
0,35453 |
0,35729 |
-2,3E-03 |
4,89E-04 |
-0,3% |
0,08% |
24 |
4,6 |
0,3912 |
0,35991 |
0,35515 |
0,3604 |
-4,8E-03 |
4,87E-04 |
-0,7% |
0,07% |
25 |
4,8 |
0,4381 |
0,36977 |
0,36237 |
0,37024 |
-7,4E-03 |
4,71E-04 |
-1,1% |
0,07% |
26 |
5 |
0,5 |
0,38771 |
0,37751 |
0,38815 |
-1,0E-02 |
4,39E-04 |
-1,6% |
0,07% |
27 |
5,2 |
0,5787 |
0,41517 |
0,40201 |
0,41556 |
-1,3E-02 |
3,89E-04 |
-2,0% |
0,06% |
28 |
5,4 |
0,6761 |
0,45364 |
0,43735 |
0,45396 |
-1,6E-02 |
3,21E-04 |
-2,5% |
0,05% |
29 |
5,6 |
0,7941 |
0,50468 |
0,4851 |
0,50491 |
-2,0E-02 |
2,33E-04 |
-3,0% |
0,04% |
30 |
5,8 |
0,9347 |
0,56995 |
0,54689 |
0,57007 |
-2,3E-02 |
1,23E-04 |
-3,5% |
0,02% |
31 |
6 |
1,1 |
0,65116 |
0,62445 |
0,65115 |
-2,7E-02 |
-8,72E-06 |
-4,1% |
0,00% |
Результаты решения представлены на рис. 2.1.

ЛИТЕРАТУРА
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: Лаборатория Базовых Знаний, 2001 г. - 632с.
Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения): Учебное пособие для вузов. - . М.: Высшая школа, 2001 г. - 382 с.
Зеленский К.Х., Игнатенко В.Н., Коц А.П. Компьютерные методы прикладной математики. – К.: Дизайн-В, 1999. –352 с.
Математика и САПР: В 2-х кн. Кн. 1. Пер. с франц. / Шенен П.,Коснар М., Гардан И и др. –М.:Мир, 1988. –204 с.
Математика и САПР: В 2-х кн. Кн. 2. Пер. с франц. / Жермен-Лакур П., Жорж П.Л., Пистр Ф., Безье П. –М.:Мир, 1989. –264 с.
Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. -Томск: МП "Раско", 1991.-272 с.
Челабчи В.В., Челабчи В.Н. К вопросу моделирования динамики нелинейных систем с сосредоточенными параметрами / Матеріали I Міжнародної науково-практичної конференції “ Наука: теорія та практика –2006”. Том 3. – Дніпропетровськ:Наука і освіта, 2006. с.51-53.
