МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ОДЕССКИЙ НАЦИОНАЛЬНЫЙ МОРСКОЙ УНИВЕРСИТЕТ

Кафедра «Техническая кибернетика»
Домашнее задание
по дисциплине « Математические методы и модели»
Выполнил
Ст. 4 к. СМ фак.
######### #. #.
Одесса 2013
СОДЕРЖАНИЕ
С.
1 ИДЕНТИФИКАЦИЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 3
1.1 Исходные данные для идентификации 3
1.2 Методика идентификации 4
2 ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 1 ПОРЯДКА 10
2.1 Аналитическое решение уравнения (2.1) 10
2.2 Численные решение уравнения (2.1) 10
1 Идентификация обыкновенного дифференциального уравнения первого порядка
1.1 Исходные данные для идентификации
Таблица 1.1 – Исходные данные
i |
|
X |
Y |
|
i |
|
X |
Y |
|
i |
|
X |
Y |
1 |
0 |
0,914 |
0,1905 |
|
36 |
3,5 |
0,5282 |
0,4498 |
|
71 |
7 |
1,5535 |
1,326 |
2 |
0,1 |
0,8795 |
0,2519 |
|
37 |
3,6 |
0,5602 |
0,4819 |
|
72 |
7,1 |
1,5676 |
1,3331 |
3 |
0,2 |
0,8379 |
0,3342 |
|
38 |
3,7 |
0,584 |
0,4724 |
|
73 |
7,2 |
1,5898 |
1,3491 |
4 |
0,3 |
0,8149 |
0,3635 |
|
39 |
3,8 |
0,6024 |
0,4742 |
|
74 |
7,3 |
1,6019 |
1,3722 |
5 |
0,4 |
0,7787 |
0,4257 |
|
40 |
3,9 |
0,6324 |
0,5136 |
|
75 |
7,4 |
1,6042 |
1,401 |
6 |
0,5 |
0,7461 |
0,4587 |
|
41 |
4 |
0,6564 |
0,516 |
|
76 |
7,5 |
1,5889 |
1,4058 |
7 |
0,6 |
0,6969 |
0,48 |
|
42 |
4,1 |
0,695 |
0,53 |
|
77 |
7,6 |
1,6073 |
1,423 |
8 |
0,7 |
0,6907 |
0,5041 |
|
43 |
4,2 |
0,7163 |
0,5592 |
|
78 |
7,7 |
1,5857 |
1,4681 |
9 |
0,8 |
0,643 |
0,5005 |
|
44 |
4,3 |
0,7695 |
0,5791 |
|
79 |
7,8 |
1,6107 |
1,455 |
10 |
0,9 |
0,6323 |
0,5102 |
|
45 |
4,4 |
0,7868 |
0,594 |
|
80 |
7,9 |
1,5827 |
1,4879 |
11 |
1 |
0,5903 |
0,5184 |
|
46 |
4,5 |
0,8297 |
0,6198 |
|
81 |
8 |
1,5792 |
1,4971 |
12 |
1,1 |
0,5775 |
0,5215 |
|
47 |
4,6 |
0,8604 |
0,6225 |
|
82 |
8,1 |
1,5796 |
1,5107 |
13 |
1,2 |
0,5367 |
0,5335 |
|
48 |
4,7 |
0,8962 |
0,653 |
|
83 |
8,2 |
1,5775 |
1,5031 |
14 |
1,3 |
0,52 |
0,5358 |
|
49 |
4,8 |
0,9268 |
0,6806 |
|
84 |
8,3 |
1,5389 |
1,4992 |
15 |
1,4 |
0,4921 |
0,5441 |
|
50 |
4,9 |
0,9669 |
0,6918 |
|
85 |
8,4 |
1,5258 |
1,5251 |
16 |
1,5 |
0,4916 |
0,5304 |
|
51 |
5 |
0,9986 |
0,7214 |
|
86 |
8,5 |
1,5176 |
1,5071 |
17 |
1,6 |
0,4751 |
0,5334 |
|
52 |
5,1 |
1,0243 |
0,7607 |
|
87 |
8,6 |
1,4983 |
1,5195 |
18 |
1,7 |
0,4392 |
0,5082 |
|
53 |
5,2 |
1,0699 |
0,7745 |
|
88 |
8,7 |
1,4807 |
1,5243 |
19 |
1,8 |
0,4509 |
0,5122 |
|
54 |
5,3 |
1,0987 |
0,8074 |
|
89 |
8,8 |
1,4581 |
1,5119 |
20 |
1,9 |
0,4155 |
0,5026 |
|
55 |
5,4 |
1,1405 |
0,841 |
|
90 |
8,9 |
1,4361 |
1,5126 |
21 |
2 |
0,4251 |
0,5101 |
|
56 |
5,5 |
1,185 |
0,8636 |
|
91 |
9 |
1,3942 |
1,5025 |
22 |
2,1 |
0,4006 |
0,4831 |
|
57 |
5,6 |
1,2099 |
0,8988 |
|
92 |
9,1 |
1,3643 |
1,4735 |
23 |
2,2 |
0,4176 |
0,4687 |
|
58 |
5,7 |
1,2411 |
0,9344 |
|
93 |
9,2 |
1,3431 |
1,4827 |
24 |
2,3 |
0,4044 |
0,4604 |
|
59 |
5,8 |
1,2828 |
0,9511 |
|
94 |
9,3 |
1,3074 |
1,4565 |
25 |
2,4 |
0,4041 |
0,4555 |
|
60 |
5,9 |
1,3004 |
0,9827 |
|
95 |
9,4 |
1,2961 |
1,4385 |
26 |
2,5 |
0,4018 |
0,4715 |
|
61 |
6 |
1,3386 |
1,0337 |
|
96 |
9,5 |
1,2617 |
1,43 |
27 |
2,6 |
0,4132 |
0,4522 |
|
62 |
6,1 |
1,3761 |
1,0471 |
|
97 |
9,6 |
1,2149 |
1,4181 |
28 |
2,7 |
0,421 |
0,4591 |
|
63 |
6,2 |
1,3927 |
1,0844 |
|
98 |
9,7 |
1,1904 |
1,3879 |
29 |
2,8 |
0,4085 |
0,4592 |
|
64 |
6,3 |
1,4249 |
1,1265 |
|
99 |
9,8 |
1,1464 |
1,3649 |
30 |
2,9 |
0,4219 |
0,4536 |
|
65 |
6,4 |
1,4509 |
1,1576 |
|
100 |
9,9 |
1,1074 |
1,3521 |
31 |
3 |
0,4389 |
0,4487 |
|
66 |
6,5 |
1,4645 |
1,1878 |
|
|
|||
32 |
3,1 |
0,4669 |
0,4303 |
|
67 |
6,6 |
1,4988 |
1,2225 |
|
|
|||
33 |
3,2 |
0,4855 |
0,4508 |
|
68 |
6,7 |
1,5125 |
1,2497 |
|
|
|||
34 |
3,3 |
0,4823 |
0,449 |
|
69 |
6,8 |
1,5327 |
1,2504 |
|
|
|||
35 |
3,4 |
0,5208 |
0,4468 |
|
70 |
6,9 |
1,5526 |
1,304 |
|
|
|||
где - значение безразмерное время ;
X - значения воздействия (в безразмерном виде);
Y - значения реакции объекта (в безразмерном виде).
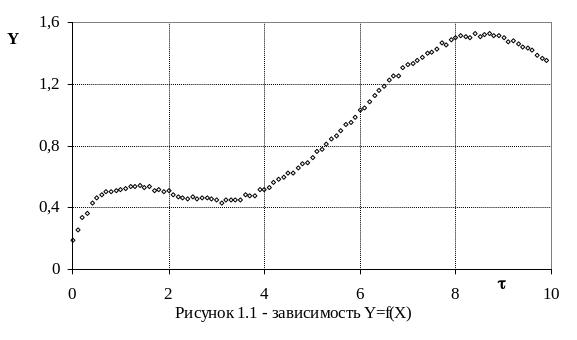
Данные таблицы отражены на рис. 1.1.