Модуль деформаций бетона
В бетоне, как в материале упруго-пластическом, имеет место нелинейная зависимость между напряжениями и деформациями.
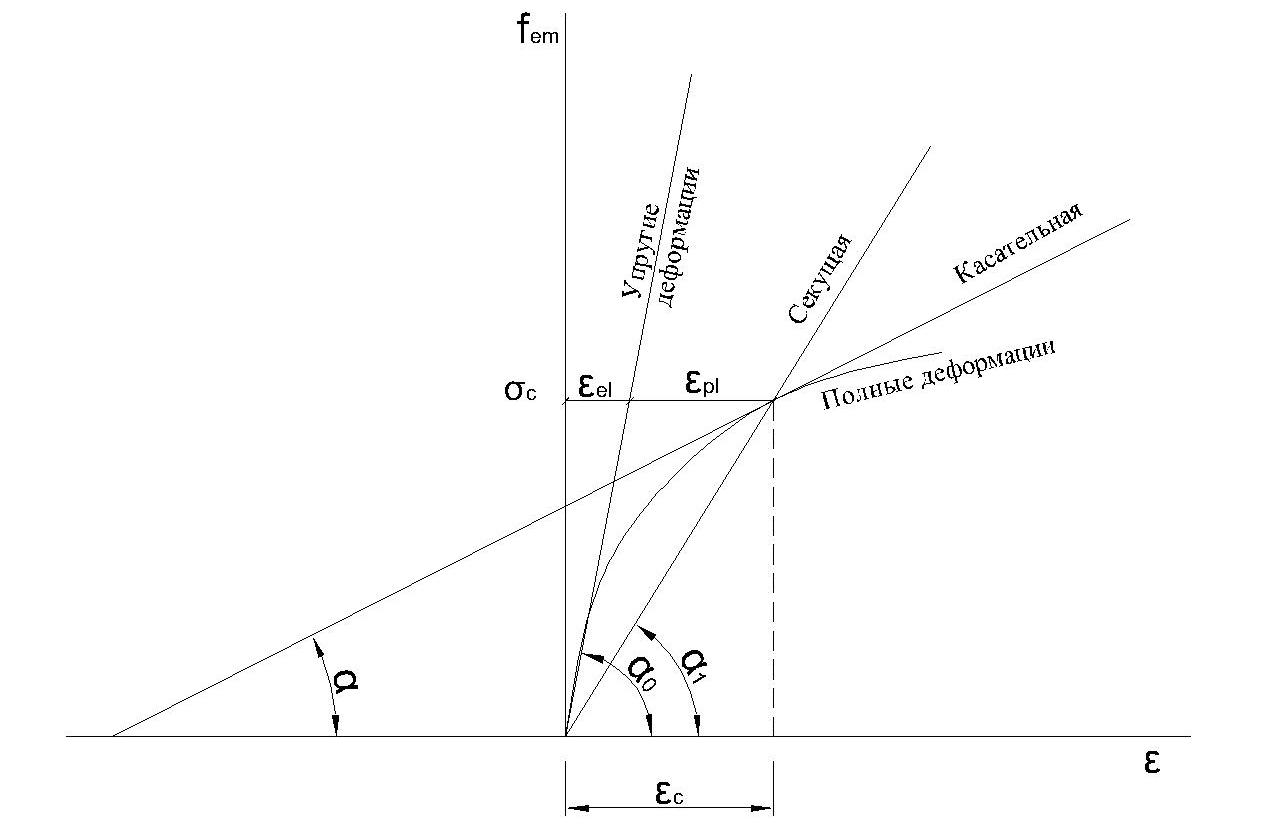
Рисунок 3.13
Начальный
модуль упругости бетона
соответствует лишь мгновенному загружению
образца, при которой возникают только
упругие деформации.
Геометрически
выражается тангенсом угла наклона
прямой упругих деформаций (рис. 3.13)
;
при этом напряжение в бетоне, выраженное
через упругие деформации
(3.4)
При длительном действии нагрузки в связи с развитием пластических деформаций модуль полных деформаций бетона становится переменной величиной и геометрически может быть выражен тангенсом угла наклона касательной к кривой в точке с заданным напряжением:
.
Следовательно,
модуль деформаций бетона
представляет собой производную от
напряжения по деформациям
Пользуясь переменным модулем деформаций , можно было бы находить деформации интегрированием функции
,
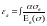но практически такой способ определения деформаций затруднителен, т.к. здесь необходима аналитическая зависимость
По предложению В.И. Мурашева, при расчете Ж.Б.К. пользуются средним модулем упруго-пластичности бетона:
,
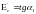представляющим собой тангенс угла наклона секущей к кривой полных деформаций в точке с заданным напряжением.
Напряжения в бетоне, выраженное через полные деформации и модуль упруго-пластистичности бетона,
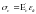(3.5)
Выражая одно и тоже напряжение в бетоне через упругие деформации по формуле (3.4) и полные деформации по формуле (3.5) установим что
(3.6)
Отсюда модуль упруго-пластичности бетона
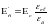(3.7)
Вводя
понятие коэффициента пластичности
бетона
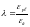и коэффициента упругости бетона
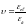и принимая во внимание, что
,
из формулы (3.7) получим
(3.8)
Для
идеально упругого материала
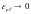и
;
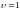для идеально пластического материала
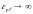и
.
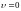Для
бетона - материала упруго-пластического
- величина
зависит от величины напряжений и
длительности действия нагрузки
.
Опыты
с бетонными призмами показывают что
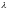может изменятся от минимального значения
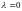до своего максимального значения при
длительном действии нагрузки
.
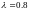Модуль упругости для тяжелого бетона естественного твердения можно определить по эмпирической формуле:
(3.9)
Модуль сдвига бетона
,
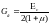(3.10)
при
коэф. поперечных деформаций (коэф.
Пуассона)
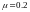он принимается равным 0,4Eв.
Мера
ползучести бетона при сжатии
применяется для определения деформации
ползучести в зависимости от напряжения
в бетоне:
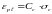(3.11)
Из выражения
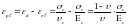
Найдем значения характеристики ползучести
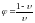(3.12)
и значение меры ползучести бетона
(3.13)
Мера ползучести бетона зависит от его марки, уровня напряжений и является переменной во времени.