Статистический ряд кубиковой прочности бетона

Границы интервалов кубиковой прочности бетона, , МПа	Количество образцов,
29,5 - 30,5	1
30,5 - 31,5	2
31,5 - 35,2	4
32,5 - 33,5	7
33,5 - 34,5	9
34,5 - 35,5	13
35,5 - 36,5	18
36,5 - 37,5	23
37,5 - 38,5	31
38,5 - 39,5	38
39,5 - 40,5	48
40,5 - 41,5	45
41,5 - 42,5	39
42,5 - 43,5	30
43,5 - 44,5	26
44,5 - 45,5	19
45,5 - 46,5	13
46,5 - 47,5	11
47,5 - 48,5	7
48,5 - 49,5	4
49,5 - 50,5	2
Всего образцов	390

Рисунок 2.7 -Гистограмма кубиковой прочности бетона

Графическое представление статистического ряда получило название «гистограмма». На графику по оси абсцисс откладывают интервалы прочностного показателя , по оси ординат - количество результатов в данном разряде. Пример построения гистограммы представлен на рис. 2.7.

Площадь гистограммы представляет собой общее количество результатов в определенной шкале. Гистограмма дает четкую картину разброса результатов или точнее распределение данного прочностного показателя.

Если количество испытанных образцов или результатов опытов достаточно велико (порядка, десятков тысяч результатов), то гистограмма может приобретать вид непрерывной кривой распределения. Для ее описания чаще всего используют закон нормального распределения или кривую распределения Гаусса. Закон нормального распределения достаточно объективно отражает действительное распределение прочности и очень полезный при изучении прочностных характеристик материалов.

Уравнение кривой распределения Гаусса имеет вид

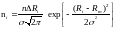; … (2.15)

где - количество результатов в интервале;

- общее количество результатов ;

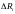- интервал значений ;

- среднее значение показателя прочности (среднее арифметическое по всем испытанным образцом);

; … (2.16)

- среднее квадратическое отклонение (стандарт);

. … (2.17)

Кривая нормального распределения представлена на рис. 2.8. Она симметрична относительно среднего и бесконечна до плюса и минуса.

Площадь под кривой между определенными значениями прочности, которые измеряются стандартными отклонениями , как и на гистограмме, представляют собой количество результатов которые разместились в данном интервале. Так, интервал прочности 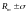включает 68,26% всех результатов испытаний, интервал , а интервал всего объема испытаний. Во многих случаях необходимо знать количество стандартов , при которых интервал содержит 90% результатов. Такому объему результатов отвечает .

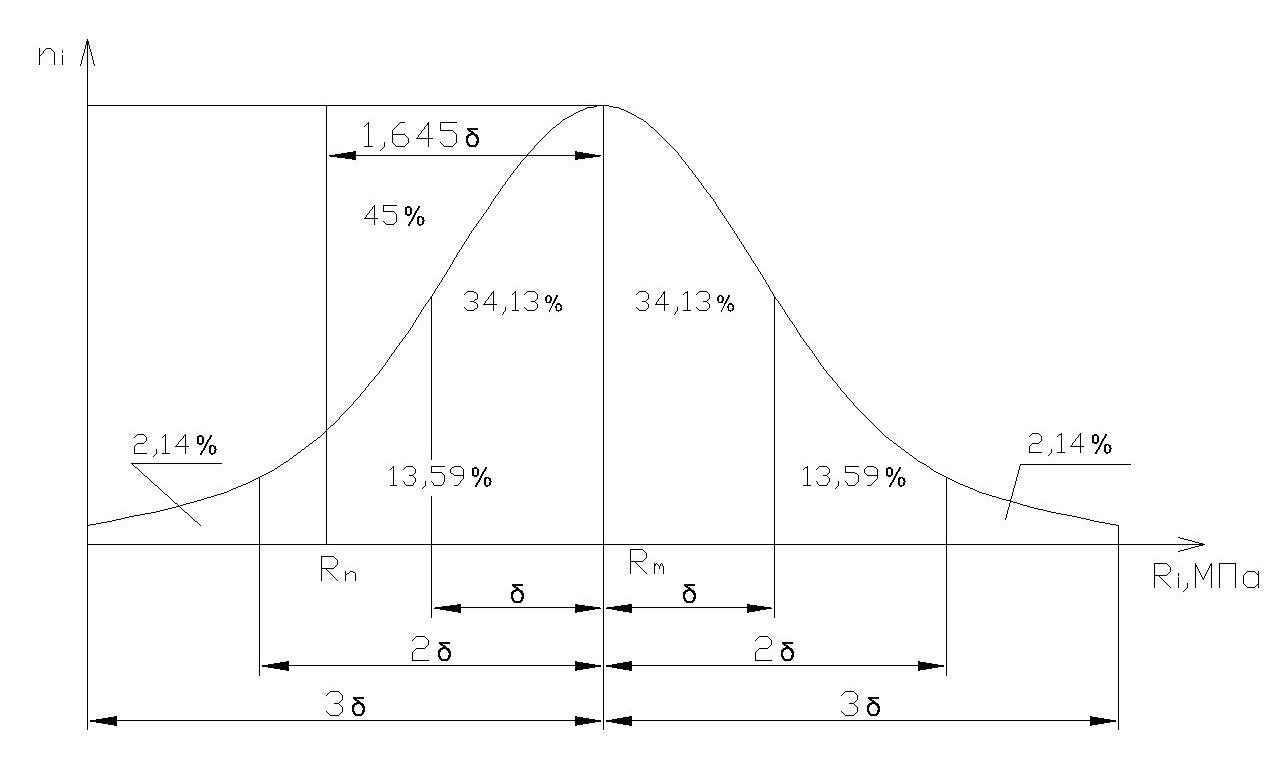
Рисунок 2.8 -Кривая нормального распределения

Следует отметить, что за границей указанных 90% остаются, как и более высокие значения прочности, так и меньшие. Очевидно, что и те и другие составляют по 5%. Естественно при нормировании прочностных характеристик принимают к вниманию только те значения , которые расположены ниже границы, которая отвечает прочности . Поэтому в случае необходимости 95% всех результатов которые включают значения не ниже величины , в нормах проектирования широко используют число стандартов или его округленное значение (1,64 или 1,65). В таких случаях говорят, что обеспеченность данного показателя составляет 0,95 или 95%.

Рассматривая прочностные свойства материалов, считают фактически невероятным отклонение случайной величины от математического ожидания более чем, на , что составляет более 99,73%. Поэтому величина 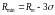представляет собой практически возможную границу снижения прочностного параметра.

Вместо стандартного отношения часто используют его относительную величину (коэффициент вариации)

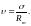(2.18)

В качестве нормируемых прочностных характеристик материалов приняты нормативные и расчетные сопротивления.

Нормативное сопротивление материала - граничное (минимально допустимое) напряжение, которое воспринимает данный материал с обеспеченностью 95%.

Расчетные сопротивления бетона сжатию и растяжению следует определять путем деления нормативных сопротивлений бетона на частные коэффициенты безопасности по бетону , принимаемые равными:

а) при расчете по предельным состояниям первой группы:

- для бетонных конструкций - 1,8;

- для ЖБК и преднапряженных - 1,5;

б) при расчете по предельным состояниям второй группы - 1,0.

Расчетное сопротивление арматуры также определяют путем деления нормативного сопротивления на частный коэффициент безопасности для арматуры.