Вопросы для самоконтроля по теме 1
1. Дать понятие научных исследований и инновационной деятельности.
2. Коротко опишите общие сведения о научных исследований.
3. Опишите развитие деревянных конструкций.
4. В чем заключается развитие в строительстве металлических конструкций?
5. Изложите в краткой форме развитие железобетонных конструкций.
6. Понятие научного познания и определение научных проблем.
7. В чем заключается сущность методов используемых на теоретическом и практическом уровне исследований?
Тема 2
Развитие методов расчета строительных конструкций. Поперечный изгиб, продольный изгиб, кручение, материалы, прочность. Основы расчета по предельным состояниям. Нагрузки и воздействия. Параметры сопротивления материалов.
Развитие методов расчета строительных конструкций
Прочность конструкций зданий и сооружений интересовала человека с давних времен. Однако основным критерием в течение многих столетий и тысячелетий был непосредственный опыт возведения и эксплуатации зданий. Если здание длительное время эксплуатировалось и не разрушалось, то по этому принципу возводили ему подобные строения.
Наши современники зачастую с восхищением смотрят на старинные сооружения, удивляясь их конструктивными решениями. При этом иногда забывают, что неудачно спроектированы или некачественно возведенные строения часто разрушались уже в процессе строительства или в скором времени после его завершения. К нашему времени сохранились только наиболее надежные сооружения.
Множество конструктивных решений человечество заняло у природы. Бревно, упавшее через ручей, случайные лесные завалы, пещера первобытного человека помогали людям осмыслить пользу и возможность использования балочных перекрытий, стеновых ограждений, изолированного помещения.
Прежде всего, появились строения балочно-стоечной системы, которые состояли из вертикальных (стены, столбы) и горизонтальных (балки, перекрытия) элементов. Формы естественных сводов в пещерах подсказали идею сводчатых и арочных перекрытий. Лианы с их переплетением стали прообразом подвесных систем.
На рисунке 2.1–2.3 схематично показана взаимосвязь между разными конструктивными решениями. Естественно, появление тех или иных решений осуществляется хаотически. Некоторые решения известны с глубокой древности, другие осуществлены в средние столетия, а многие из них появились в последние столетия. На этих схемах воочию представлено, как из простейших конструктивных элементов могут быть получены сложные конструкции и схемы.
Логическая взаимосвязь различных стержневых элементов и конструкций показана на рис. 2.1. Такие элементы, как сжатая стойка (колонна) и элементарная балка известны с доисторических времен. С этих элементов еще в древнем мире выполнено основное конструктивное решение ордерной архитектуры – рама с шарнирным соединением горизонтального ригеля. Одновременно для перекрытия прогонов начали использовать арочные и сводчатые конструкции. Интересно отметить, что стропильная конструкция в виде треугольной формы появилась гораздо позже – в конце первого тысячелетия новой эры у народов Центральной и Восточной Европы, где основное развитие получает деревянное зодчество.
Первым исследователем (в современном понимании) в науке о прочности материалов и конструкций стал гений эпохи возрождения Леонардо да Винчи (1452-1519). Он первым осмыслил роль эксперимента для установления научной истины. Леонардо да Винчи изучал сопротивление колонн сжатию и установил, что прочность колонн прямо пропорциональна площади поперечного сечения и обратно пропорциональна ее длине. Этим впервые были установлены четкие зависимости для прочности конструкций. Кроме этого, в результате экспериментов Леонардо да Винчи первым сформулировал задачу об устойчивости сжатых элементов. Для изгиба он обнаружил взаимосвязь между длиной пролета балки и величиной разрушающего сосредоточенного усилия приложенного в середине пролета. Леонардо да Винчи испытывал на растяжение проволоку, дал описание методики испытаний, и указал какое, из этого необходимо делать заключение. Занимался он и прочностью арок, однако, не смог полностью освободится от господствующих в то время ошибочных представлений.
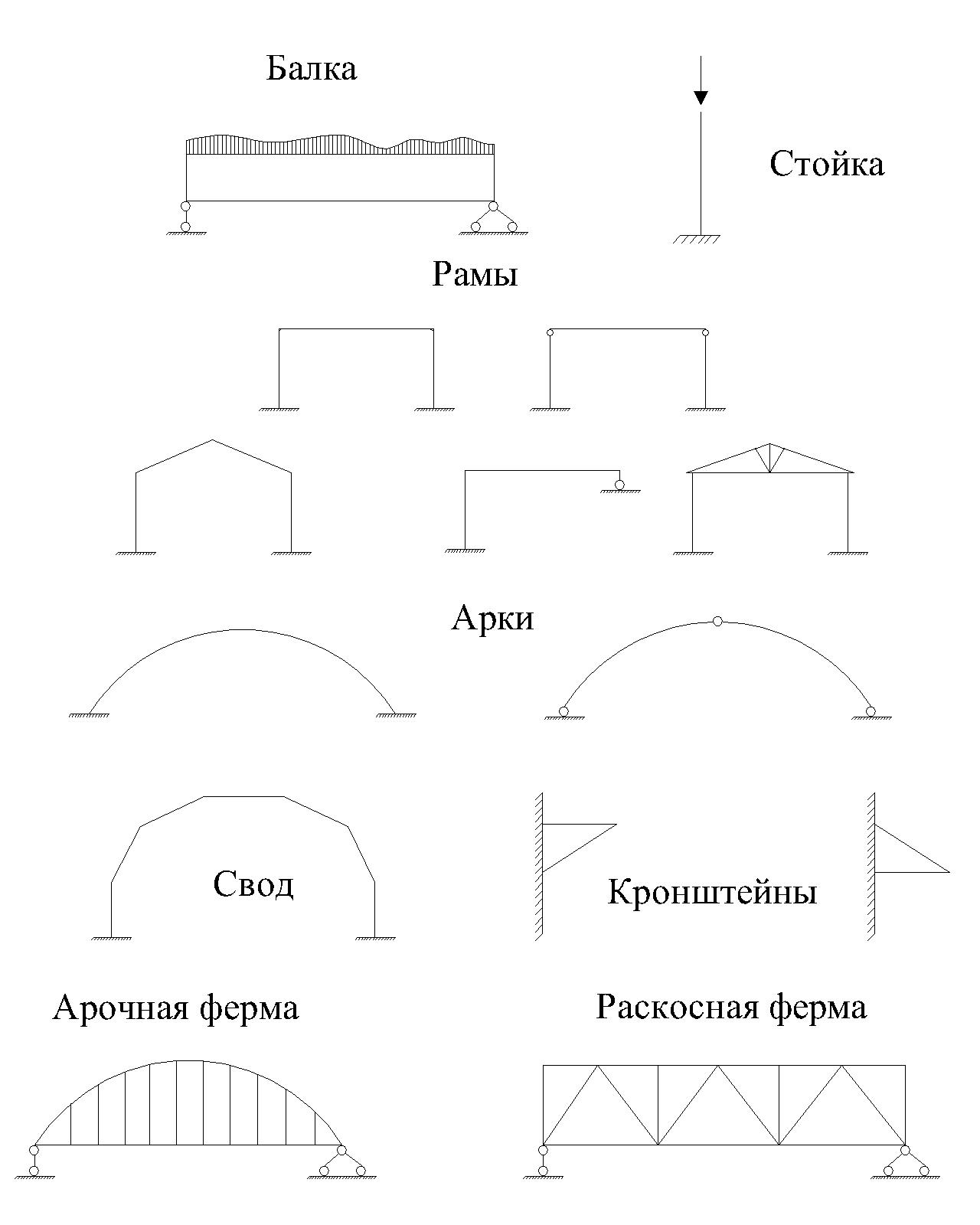
Рисунок 2.1 - Плоские стержневые системы
Рисунок 2.2 -Пространственные конструкции
Рисунок 2.3 -Нитчатые (тросовые) конструкции
Однако все эти работы остались неизвестными как современникам Леонардо да Винчи, так и последующим исследователям.
Рукописи Леонардо да Винчи были обнаружены только в XX столетии и на сегодня имеют историческую ценность. Однако, к сожалению, влияния на развитие строительной науки они не оказали.
Только лишь через два столетия - в 1638г. была опубликована книга Г.Галилея «Беседы и математические доказательства, касающихся двух новых отраслей науки, принадлежащих к механике и местного движения». Этим Галилей заложил основы «двух новых отраслей науки», а именно - динамики и науки о прочности. Короче говоря, с именем Галилея связано зарождение науки «строительная механика»; ведь механика и сопротивление материалов - разделы современной строительной механики.
Особый интерес представляет подход Галилея к проблеме прочности, которая представляет собой первые шаги сопротивления материалов.
Галилей рассматривал два вида напряженного состояния стержней - осевое растяжение и изгиб. При этом его интересовала только величина разрушающей нагрузки. Как определял сам Галилей, его трактат «относится к сопротивлению твердых тел силе, которая стремится это тело разрушить». А важные вопросы сопротивления материалов, такие как поведение стержней, в условиях нормальной эксплуатации, величина и распределение усилий при обычных нагрузках, особенности перехода от нормального состояния к разрушению - все это осталось вне внимания исследователя. Условия для постановки подобных задач еще не созрели. Поэтому первое исследования прочности было основано на граничном состоянии стержня, т.е. на изучении его стадии разрушения.
Прочностные характеристики материалов в то время еще не были известны, поэтому Галилей рассматривал влияние на прочность стержня (конструкции, элемента) только геометрические параметры - размеры поперечного сечения, длину стержня и пр. Строго говоря, изучалась сравнительная оценка прочности элемента с одного и того - же материала. Предполагаем, Галилей давал себе отчет, что прочность элемента зависит и от материала, но для соответствующих оценок у него отсутствовали предполагаемые данные о прочности материалов. Поэтому ему пришлось ограничить задачу.
Галилей исходил из того, что прочность растянутого элемента (стержня, каната) прямо пропорциональна площади поперечного сечения элемента и есть таковой, что не зависит от его длины. Нельзя не отметить, что этот раздел Галилей излагает так, будто - бы вопрос прочности растянутых элементов хорошо известен читателю. Очевидно, указанная выше зависимость была задолго до Галилея, сведения о ней переходили от поколения к поколению, от учителя к ученику, от мастера к подмастеру. Поэтому заслуга Галилея в том, что он в своей работе впервые обнародовал сведения о прочности растянутых элементов. Поскольку нам известно более ранних публикаций не выявлено. Материал этой книги дает основание считать, что Галилей понимал значение материала для прочности растянутого элемента. Прямые указания на это отсутствуют, в наличии только косвенные, однако следует предполагать, что прочность при растяжении для Галилея лишь предпосылка при решении совсем новой на те времена задачи - о прочности изгибаемого элемента. И в этом понимании он стал основоположником новой отрасли знаний - науке о прочности.
Проследим развитие мысли Галилея при решении задачи о прочности изгибаемого элемента. Вот что писал Галилей с этого явления: «… Легко уяснить причину того, что твердые цилиндры или призмы из стекла, чугуна, дерева или другого хрупкого материала, подвешенные вертикально (т.е. центрально растянутые), выдерживают довольно большую нагрузку, в то же время при горизонтальном положении (т.е. при изгибе) они - же могут быть разрушены небольшими нагрузками, и тем меньшими, чем больше длина цилиндра или призмы превышает их толщину (высоту сечения)».
Представим себе призму АВСД (рис. 2.4), закрепленной в стену своей частью АВ, на втором конце приложен груз F.
Очевидно, что призма должна изломаться, это осуществится в точке В, где граница стены есть точка опоры, а расстояние ВС есть первое плечо, с которым действует сила F. Толщина тела АВ есть вторым плечом, которое определяет сопротивление, обусловленное сцеплением частичек тела АВСД с его частицами, заделанными в стене.
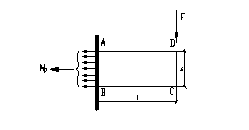
Рисунок 2.4 -Схема действия усилий при изгибе за Галилеем
… Поэтому абсолютное сопротивление призмы АВСД разрыву (под которым понимаем сопротивление действию силы в продольном направлении, при котором сила растяжения и сопротивления равны между собой) так относится к сопротивлению разрыва с помощью плеча ВС, как длина ВС к половине толщины призмы АВ или к радиусу, если взять цилиндр.
Изложим мысли Галилея с позиции современных научных публикаций.
Рассмотрено состояние современной консольной балки, нагруженной на свободном конце сосредоточенной силой F. Необходимо определить в каком месте, и при каком значении силы F балка будет разрушена.
Поскольку Галилею было известно правило ричага, то место разрушения определить легко - чем дальше плечо от точки приложения силы F, тем вероятнее место разрушения. Становится понятным, почему Галилей считал опасным местом именно опорное сечение консольной балки. Что - же сопротивляется действию силы F в опасном сечении непосредственно перед разрушением? Ответ очевиден - прочность балки в этом сечении.
Галилей принял следующую схему разрушения:
- в опасном сечении усилия сопротивления распределены равномерно по сечению;
- усилия сопротивления - растянутые (по аналогии с центральным растяжением);
- излом консоли осуществляется при образовании трещины вверху опасного сечения с последующим ее раскрытием и поворотом балки вокруг оси, что совпадает с нижней границей сечения - вокруг точки В.
Принятая схема разрушения балки приближена к реальности для хрупких материалов (камень, чугун, стекло), которые лучше сопротивляются сжатию, чем растяжению. Поскольку в результате при этом осуществляется разрыв всего сечения, то логичной является предпосылки Галилея об идентичности разрушения консоли и центрально растянутого элемента. Отсюда возникло допущение о равномерности распределения растягивающие усилий по высоте опасного сечения.
Учитывая ту обстановку, что во время Галилея (первая половина XVII ст.) о напряженном состоянии изгибаемого элемента ничего не было известно, следует надлежащее отдать Галилею, который отважился решить задачу о прочности при изгибе.
Таким
образом, в соответствии принятого
Галилеем предсказания, в опасном сечении
разрушению препятствует растягивающая
сила
.
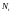По правилу ричага величина этой силы
тем большая, чем дальше расположено
сечение от точки приложения силы F.
В соответствии современных взглядов запишем уравнение, отражающее равенство суммы моментов относительно точки в непосредственно перед разрушением:
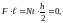… (2.1)
отсюда вытекает предложенное Галилеем соотношение
….
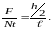(2.2)
Если
обозначить сопротивление материала
через R, то для прямоугольного сечения
имеем
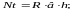т.е.
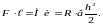… (2.3)
Иначе говоря, за современной терминологией, Галилей получил значение момента сопротивления для прямоугольника.
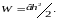… (2.4)
и для круглого сечения
… (2.5)
Современный инженер такое решение считает глубоко ошибочным. Ведь в рассматриваемом сечении не удовлетворены условия равности сил и условия равности деформаций. Прочность балки прямоугольного сечения завышена в три раза, а балки круглого сечения - в четыре раза. Вместе с тем это первое решение можно считать правильным, когда вспомним поставку задачи.
Галилей изучал неабсолютную, а сравнительную прочность геометрически подобных стержней. И именно эту задачу он правильно решил для каждого вида профиля отдельно.
Своеобразие постановки задачи позволило Галилею исключить определения прочностных характеристик материалов и поиска действительного распределения напряжений в сечении, тем более самого понятия «напряжение» тогда не существовало. Естественно, о существовании нулевой линии тогда никто не имел понятия.
Именно с Галилея началась и в дальнейшем приобрела развитие одна из основных отраслей строительной науки - строительная механика.
Позже установили, что напряжения по высоте сечения не одинаковы и являются функциями координаты по высоте (наряду с другими факторами), т.е.
σ
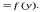… (2.6)
и где бы не проходила нулевая линия напряжений, момент сопротивления для прямоугольного сечения имеет вид
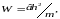… (2.7)
а
для круглого сечения
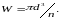… (2.8)
где m и n - числовые параметры, независимые от размеров сечения.
Эту теорему в 1718г. впервые доказал для прямоугольного профиля французский исследователь Паран (Parent).
Если
с соответствием допущения Галилея
принять
,
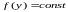то получим m=2
и n=8,
как ранее показано.
Мариотт (E. Mariotte) в 1686г. для изгиба принял треугольную эпюру напряжений, разместив нулевую (нейтральную) линию на границе сечения, т.е. допустил что . В этих условиях он получил m=3 и n=12,8.
Паран разместил нейтральную линию в середине высоты сечения при той - же зависимости и получил m=6 и n=32, то есть те значения коэффициентов, которыми пользуемся и в настоящее время.
Следует отметить, что все заключения XVII-XVIII ст. базируются при рассмотрении только симметричных профилей - прямоугольник, круг. Поэтому Паран и получил правильное решение. Несимметричные сечения, такие как тавр, или трапеция практически не применялись, поэтому исследователями они не рассматривались. Только в начале XIX ст. начали применять стальные балки подобных профилей. Задачу изгиба стержня произвольного сечения в упругой постановке вопроса решил француз Л. Навье (L. Navier), который установил, что нулевая линия всегда расположена в центре тяжести сечения.
Таким образом, решением задачи об изгибе занимались много ученых почти два столетия. Если учитывать, что отсутствовали многие понятия и много явлений приходилось открывать, станут понятными те трудности, которые предстали перед учеными.
Тяжелее всех было Галилею как первопроходцу. Естественно, первым, по сути, был Леонардо да Винчи. Однако результаты его поисков остались неизвестными, и Галилей начинал с нуля.
Следует отметить еще одно обстоятельств. Галилей считал, что любое разрушение происходит путем отрыва и обусловлено действием растягивающих усилий (точнее - напряжений). Позже, когда ввели понятие «напряжение», такой взгляд на природу прочности и разрушения получил название «первая теория прочности».
Основная роль Галилея в истории наука о прочности, следует отметить следующее:
1. Галилей рассматривал прочность статически определимой балки в стадии разрушения.
2. Место и схему разрушения он определял условно, опираясь на интуицию.
3. Сопротивление опасного сечения при изгибе определено на основе допущений, - в балке действует такое же растягивающее усилие, как и в центрально растянутом элементе.
4. Взаимосвязь между разрушающими нагрузками, размерами балки и ее прочностью он устанавливал из уравнения равновесия.
Сравнивая прочность простой балки на двух опорах с прочностью балки, опертой посредине ее длины, в качестве иллюстрации Галилей приводит схемы изгиба, представленные на рис. 2.5, что образно поясняет его подход к проблемам прочности.
Рисунок 2.5 -Разрушение балок при изгибе по Галилею
В заключении отметим основную заслугу Галилея пред наукой о прочности. Он первый (если не считать Леонардо да Винчи) предпринял попытку решить задачу прочности балки, а также пытался решить вопрос природы прочности материала. Много его положений мы считаем общепринятыми и на сегодня. Ведь и сегодня мы не имеем ответа на вопрос о природе прочности, кроме некоторых гипотез качественного характера, которые не позволяют давать количественной оценки. Естественно, теперь мы знаем намного больше Галилея, научились эмпирически определять множество параметров прочности материалов, но окончательно проблема прочности будет решена после того, когда исходя с известных физико-химических и структурных особенностей материала, исследователь сможет предусмотреть его прочностные характеристики. Однако это - дело будущего.
Прежде чем продолжать изложение о развитии методов расчета, не лишним будет отметить, что к началу XIX века проектировщики зданий и сооружений очень редко обращались к расчету конструкций. Иначе говоря, результатом научных поисков практически не влияли на проектирование. Причин этому немало.
Во-первых, строительная отрасль давно проявляет консерватизм, и даже инертность относительно различных теоретических поисков и расчетных методов, придерживаясь профессиональных традиций. Строители еще не уяснили пользы от науки и поэтому не умели предъявлять ей свои требования. Частичным оправданием могут быть те обстоятельства, что социально-экономическая обстановка в странах Европы XVII-XVIII веков не только не благоприятствовала, а преимущественно стояла на начале развития техники, в том числе и строительной.
Во-вторых, ученые, изучающие сопротивление твердых тел, не очень активно занимались практическим внедрением своих поисков. Как сегодня принято говорить, наблюдался огромный отрыв науки от практики. Ученые еще не осмыслили того, что путь развития научных идей лежит в постановке опытов, проверке практикой для подтверждения, как начальных допущений, так и правильности полученных выводов.
Об отрыве науки от практической деятельности можно судить на основе многих источников того времени. Приведем две цитаты характеризующие взаимосвязь науки и практики в отрасли строительства.
В 1727г. Готье (Gautter) опубликовал в Париже «Диссертацию о толщине мостовых сводов», в которой по поводу работы своего предшественника Делагира (о расчете сводов) написал:
«Я честно признаюсь, что недостаточно научен, чтобы понять все. Я не смог даже проследить выкладки автора, настолько они мне были сложными. И я считаю: все что он написал, не смогут понять не полуученые, не тем более рабочие. Ибо для понимания его выводов необходимо знать алгебру, какую он использовал, то не думаю, чтобы каменщик или архитектор, для которых следует писать подобные работы, могут когда-нибудь их понять и использовать».
Гораздо позже, в 1809г. Е. Готе (E. Gouthey) в своем «Курс мостостроения» отметил:
«Каждый строитель оценивает, насколько важно ему знать меру прочности материалов, поэтому раздел механики, известный под наименованием сопротивление твердых тел, обещает очень плодотворные дополнения. Много было таких, которые занимались этой наукой, однако и Л. Эйлер и Лагранж не брезговали сделать из нее предметами своих исследований, полученные результаты не давали возможности в помощи строительства. Аналитические формулы не эффективны пока не будут определены значения постоянных величин в них используемых; однако и ныне попытки их определения остаются почти бесплодными».
Эти и подобные изречения свидетельствуют, что теория и практика строительного проектирования длительное время существовали независимо один от одного.
В науке о прочности конструкций или точнее в строительной механике следующий шаг (после Галилея) сделал Р. Гук (R. Hooke), который в 1678г. опубликовал свой закон - «ut tensio, sic vis», в переводе с латыни значится: какое удлинение, такова сила. Для этого ему пришлось найти приспособление, которое отражало бы больше деформации, - винтовую пружину. Наблюдая за поведением пружины под нагрузкой, Гук вывел закон пропорциональности между нагрузкой и деформаций.
Кроме этого, своим законом Гук установил еще одну, неизвестную ему особенность твердых тел - упругость. Между прочим, до XIX века научные поиски, основанные на законе Гука, были вне внимания инженеров-строителей, для них они были абстрактными, оторванными от реальной жизни и неприспособленными к практике.
И только когда в 1807г. англичанин Т. Юнг (T. Young) ввел численную характеристику упругости - модуль Юнга (модуль упругости), тогда и появилась возможность практического использования закона Гука.
Строительную механику в те времена интересовала проблема прочности, т.е. предельное состояние тела в стадии разрушения. Теория упругости и ученье о прочности развивалось независимо одно от другого. С одной стороны, идет изучение упругих деформаций тел, но это никак не повязано с прочностью. С другой стороны, исследование предельных состояний конструкций (излом балки, разрушение свода) вполне обходилось без понятия упругости. Этот взаимный разрыв двух разделов одной науки был основной причиной того, что строительная механика еще не стала прикладной наукой.
Независимо и практически одновременно с Гуком в 1680г. закон пропорциональности открыл Мариотт (E. Mariotte). Однако приоритет Гука сегодня общепризнанный.
Мариотт вместе с тем выдвинул еще одну очень важную гипотезу. Он озвучил допущения, что растянутый стержень разорвется тогда, когда его удлинения превысят некоторую безопасную границу, и обосновал это допущение путем размышления о силах притяжения между частицами тела. При взаимном удалении частиц силы притяжения слабеют, что приводит к разрыву стержня. Сегодня эту гипотезу называют «второй теорией прочности».
Самым важным наследием закона Гука - Мариотта явилось установление пропорциональности между изгибающим моментом и кривизной линии прогибов. Эту зависимость получил Я. Бернулли (J. Bernoulli). Для ее доказательства в 1695г. Бернулли принял гипотезу плоских сечений, которая положена в основу современных расчетов на изгиб и носит его имя - гипотеза Бернулли.
Задача о деформации изгиба играет огромную роль в строительной механике, поскольку на ее решениях основана вся современная теория статически неопределенных систем. Однако в XVII веке она оказалась весьма ранней, практического внедрения не находила и длительное время оставалась предметом абстрактных действий математиков.
В течение всего XVIII столетия изучение упругих деформаций твердых тел оставалось чисто научной проблемой. А техническим заданием были попытки решить задачу прочности балки и сводов.
Таким образом, основным объектом исследований в то время была прочность конструкций, или, как мы сейчас говорим, предельное состояние конструкций по прочности. При этом вопросе прочность материалов пока что даже не затрагивалась. Естественно, многие ученые догадывались о влиянии прочности материала на прочность конструкции, однако это положение никто четко не сформулировал, поэтому изучение прочностных свойств материалов началось гораздо позже, уже в XIX веке.
Поведение ж конструкций в рабочем состоянии изучалось стихийно, под влиянием общего развития механики и математики.
Одним из первых исследователей, который начал более - менее систематическое экспериментальное изучение прочности материалов и на этой основе определять закономерность работы конструкций был французский военный инженер Ш. - О. Кулон (S. - O. Coulomb). В 1773г. он опубликовал работу «Опыт применения правил максимуму и минимуму к некоторым вопросам статики, приналожных к архитектуре», где рассмотрены следующие вопросы:
- теория прочности материалов;
- теория изгиба балок;
- теория отпора грунта на подпорную стенку;
- теория расчета сводов.
Кулон привел испытания образцов из камня и известкового раствора. Образцы в виде «восьмерок» испытывались на осевое растяжение, а в виде призм - на срез и изгиб. Кулон получил близкие значения границ прочности при растяжении и срезе, поэтому он принял их одинаковыми.
Сопротивление
сжатию Кулон попробовал объяснить
силами сцепления и силами трения. В
призме, центрально нагруженной сжимающей
силой F,
Кулон рассматривает наклонное сечение,
составляющие угол α с нормальным
сечением. Внешнюю силу F
он раскладывает на две составляющие:
нормальную к наклонному сечению F
cosα
и касательную
к тому же сечению F
sinα.
Последняя
стремится сдвинуть верхнюю часть призмы,
поэтому осуществляет сопротивление
материала сдвигу Т
и силы трения
от действия нормальной составляющей.
Если
обозначить коэффициент трения через
,
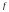то по Кулону, получим тангенс угла
наклона опасного сечения:
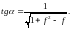… (2.9)
Поскольку у Кулона собственных исследований (опытов) со сжатыми элементами не было, для сопоставления опытных данных с прогнозируемыми теоретическими он использует результаты испытаний Питера Мушенбрука, в которых находит подтверждение своих теоретических выводов.
Изучаючи изгиб балки, Кулон из условия равенства нулю суммы проекций сил на продольную ось бруса определяет положение нейтральной оси. По всей видимости, он не знал, что Паран еще в 1713г. (60 лет ранее) нашел правильное решение задачи об изгибе балки прямоугольного профиля. Кулон принял выпуклые криволинейные эпюры напряжений, как в сжатой, так и в растянутой зонах. Для случая упругих материалов он принял прямолинейную эпюру напряжений и вслед за Параном получил правильное значение момента сопротивления. Кулон указал, что сжатая зона должна быть такой величины, чтобы она могла воспринять приходящуюся на нее сжимающую силу. Задачу о прочности балки он предлагает рассчитывать по своей теории прочности материала при сжатии.
В задаче о давлении грунта на подпорную стенку Кулон предлагает учитывать трение и сцепление грунта. Как он отметил, в этой задаче использован тот самый метод, что и у теории прочности материала. Много положений Кулона о давлении сыпучих материалов, о линии их рушения и другие сведения используются и в современной расчетной практике.
В последней задаче Кулон рассматривает расчет прочности свода каменной кладки, где снова ж учитывает трение и сцепление в швах.
Таким образом, своими исследованиями Кулон внес большой вклад в развитие строительной механики. Он показал, что разрушение сжатого стержня часто происходит вследствие сдвига, и выразил допущение, что причиной какого-нибудь разрушения является сдвиг.
Обнаруживши существование касательных напряжений (или как он выражался усилий), Кулон сумел дать первое решение задачи о прочности круглой проволоки при кручении. Кроме этого, с опытов на изгиб и кручение он установил пропорциональность между нагрузкой и упругой частью деформаций вплоть до разрушения.
Предложенные Кулоном идеи в отношении влияния касательных напряжений (сдвига) в дальнейшем получим наименование «третья теория прочности».
Что касается экспериментальных исследований, то в XVIII веке мало кто занимался экспериментальным изучением проблем прочности. Отдельные опыты проводили Гук, Мариотт и другие ученые. Первым исследователем - экспериментатором был профессор Лейденского университета П. Мушенбрук (P. Van Musehenbroek). Он изобрел испытательную машину, в которой испытывал прочность разнообразных материалов и элементов. Результаты испытаний длинных стержней на сжатие позволили ему обнаружить явление продольного изгиба и установить, что критическая сила обратно пропорциональна квадрату длины стержня. Этим Мушенбрук первым начал (положил в основу) изучение проблемы стойкости сооружений.
Первым задачу продольного изгиба в 1774г. решил Л. Эйлер (L. Euler), швейцарец по происхождению проработавший почти всю жизнь в Петербургской академии наук. Эйлер занимался исследованиями в области математики, был создателем вариационного исчисления. В строительной механике его имя связано с задачей продольного изгиба. Он изучал формы кривых, удовлетворяющих условия минимума потенциальной энергии, и по этим формам определял уравновешенную нагрузку. Одна из девяти форм кривых, которые изучал Эйлер, уравновешивалась двумя равными и противоположно направленными сжимающими силами, приложенными по концам дуги. Эйлер сразу - же заметил, что этот случай отвечает задаче о продольном изгибе или, по словам автора, «Задаче о силе колонн». К рассмотрению задач продольного изгиба Эйлер возвращался дважды - в публикациях 1757г. и в 1778г.
Дальнейшего развития задача о продольном изгибе получила в работах французского математика Лагранжа (Lagrange), где приведен точный интеграл уравнения продольного изгиба, получены в зависимости между стрелой прогиба и величиной нагрузки. Лагранж первым определил возможность продольного изгиба по некоторых полуволнах и получил значение критической силы для разных условий закрепления стержня по концам.
Нельзя не отметить француза С.Д. Пуассона (S. D. Poisson), который в 1811г. ввел понятие «механическое напряжение» как внутреннего усилия, отнесенного в единице площади сечения. Кроме этого, открыл наличие поперечных деформаций и сформулировал зависимость между продольной и поперечной деформацией.
Таким образом, в области строительной механики на начало XIX века было выполнено много основополагающих открытий. Подытожим все выше сказанное.
Изгиб. Предложены различные способы расчета балок прямоугольного и круглого сечений для элементарных схем нагружения - консоль с нагрузкой на конце и обычная с нагрузкой в середине пролета. Пока еще нет четкого разграничения между параметрами жесткости при изгибе (моментом сопротивления) и параметром прочности (моментом сопротивления). Даже определение размерности этих параметров не всегда правильное. До 1807г. отсутствует понятие модуля упругости, а конкретные его величины (значения) не определен даже для наиболее распространенных строительных материалов (камень, древесина).
Продольный изгиб. Обнаружено явление продольного изгиба, получено правильное решение задачи Эйлера-Лагранжа в упругой постановке.
Кручение. Правильное решение Кулона для элементов круглого поперечного сечения не имеет количественных оценок в виду отсутствия сведений о сопротивлении материалов срезу, а основное - отсутствие самого понятия о модуле сдвига.
Материалы. Открыто явление упругости, касательные напряжения (сдвиговые усилия, как тогда выражалось) и одновременно с этим - полное отсутствие сведений о прочностных и деформативных характеристиках материалов.
Прочность. Изложены три спорные теории прочности.
С одной стороны - итоги впечатляющие, с другой - совсем незначительные в отношении практического использования. Дабы точнее оценить ситуацию, напомним: вплоть до начала XIX века внимание исследователей было уделено только проблемам прочности. Ученые в основном рассматривали только стадию разрушения (предельное состояние по прочности) конструкций. Рабочее состояние этих конструкций их интересовало значительно меньше.
Такие основные итоги первого периода в истории развития строительной механики: основное внимание уделялось вопросам разрушения конструкций; изучение конструкций в рабочем состоянии проводилось эпизодически, очень непоследовательно - над всеми «висел грузом» авторитет Галилея.
Первым отважился отойти от основного подхода Галилея к проблеме прочности, т.е. рассмотрение предельного состояния конструкций по прочности, французский ученый Л. Навье (L. Havier). Он принял новый подход, основанный на рассмотрении рабочего состояния конструкций - рассматривалась стадия ее нормальной эксплуатации. С именем Навье связано начало второго периода в развитии строительной механики.
Новый период строительной механики начался в 1826г., когда Л. Навье опубликовал свой курс лекций с прикладной механики. В этой работе в качестве основной расчетной стадии впервые приняли стадию рабочего состояния конструкций. Это автору дало возможность получить надежный расчетный аппарат, пригодный для практического использования.
Теория Навье, которая определила пути развития строительной механики на столетия вперед и получила наименование классической, базировалась на таких положениях:
- сопоставление наибольших напряжений от внешних нагрузок в стадии эксплуатации с допустимыми напряжениями для данного материала - принцип Навье;
- рабочее состояние и стадия разрушения в целом подобны, поэтому отношение усилий, напряжений и деформаций в этих стадиях одинаковы - допущения Навье;
- сечения, плоские к деформациям, остаются плоскими и после деформаций - гипотеза Я. Бернулли;
- напряжения пропорциональны относительным удлинениям или укорочениям - закон Р. Гука.
Сущность методики, разработанной Л. Навье заключается в том, чтобы удовлетворить условие
…
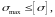(2.10)
где
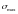- наибольшее напряжение в сечении
элемента, вызванное воздействием внешних
нагрузок;
-
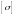допускаемое напряжение для материала
элемента, полученное непосредственно
из опытов.
Помимо создания науки о сопротивлении материалов, Л. Навье заложил основы нового раздела строительной механики - теории упругости.
Принятый им принцип малых перемещений совместно с законом Гука благоприятствовал развитию теории упругости, которая с первых шагов изучает только рабочее состояние конструкции, полностью отказавшись от рассмотрения стадии разрушения. В этом и лежит основная ценность теории упругости: появилась возможность решать много важных вопросов по проектированию конструкций. Однако в этом и ее основной недостаток: отказ от рассмотрения стадии разрушения не даст возможности ответить на вопрос (очень важный) о величине запаса прочности конструкций и ее работоспособности.
Основные достижения строительной механике XIX века можно коротко перечислить, не вдаваясь к детальному рассмотрению каждой задачи.
Сен-Венан (Sant-Venant), ученик Л. Навье, в 1843г. решил задачу косого изгиба; он же много сделал для развития теории упругости и на ее основе решил много задач напряженного состояния конструкций.
Задачу о внецентренном сжатии и внеценренном растяжении в общем виде первым в 1854г. решил Шарль Бресс (Bresse); он же ввел понятие о ядре сечения. Бресс первым нашел подход к решению задачи статически неопределимых систем методом сил, указал способы определения количества неизвестных и сформулировал понятия о равенстве совместности деформаций. Он же впервые в 1848г. начал применять эпюры моментов и других внутренних усилий.
Первое решение задачи о поперечном изгибе с учетом касательных напряжений в 1855г. получил российский ученый Д.И. Журавский, формулу которую для вычисления касательных напряжений широко применяют в современных расчетах конструкций.
В 1857г. француз Клайперон (Clapeyron) получил уравнение трех моментов, завершивши создание теории неразрезных балок.
Работами англичанина Максвелла (Maxwell) и итальянца Кремоны (Cremona) в 1864г. разработан графо-аналитический метод расчета статически определимых ферм. Максвелл также создал методику расчета статически неопределимой фермы, представил уравнения деформаций в каноничной форме и указал общий метод вычисления перемещений как коэффициентов канонических уравнений метода сил.
Работы многих исследователей - Бресса, Клайперона, Максвелла, Кастильяно (Castilliana), Мора (Mohr) и др. - позволили разработать удобный метод вычисления перемещений, давши тем самим мощный толчок развития метода сил.
Начатые еще Эйлером исследования устойчивости сжатых стержней развил и фактический завершил российский ученый Ф.С. Ясинский (поляк по происхождению), опубликовавший в 1894г. работу «Опыт развития теории продольного изгиба», в которой привел формулы к вычислению критической силы, которые используются и теперь.
В этот же период началось рождение другого основного метода расчета статически неопределимых систем - метода перемещений.
Бресс в 1865г. получил уравнение трех углов для неразрезной балки. Однако на эту работу не обратили надлежащего внимания. Только через 20 лет при расчете статически неопределимых ферм (ферм с жесткими узлами) начали использовать углы поворотов узлов в качестве основных неизвестных. Это были первые шаги по созданию метода перемещений. Основные же исследования и разработка метода перемещений осуществлены в начале XX века.
Таким образом, вторая половина XIX века ознаменовалась повсеместным определением принципа расчета по рабочим состояниям (расчет по допускаемым напряжениям).
В период конца XIX и начала XX века характерным является быстрое развитие теории устойчивости сооружений, накопление опытных данных о прочности, усталости и пластичности материалов. Инженеры получили в свое распоряжение надежный расчетный аппарат, гарантирующий прочность конструкций. Это обстоятельство сыграло решающую роль в течение многих десятилетий.
Обеспечить прочность конструкций любой ценой - таков был общий подход, даже когда эта цена была значительно выше возможного минимума. Естественно, такой подход приводил к большим запасам прочности, но гарантировал от разрушения конструкций, зданий и сооружений.
Естественно, так долго продолжатся, не могло. Когда после первой мировой войны во всех странах резко возросли объемы строительства, игнорирование экономических показателей стало невозможным. В это время сформулировано главное назначение строительной механики как прикладной науки - обеспечить достаточную надежность конструкций при минимальной затрате материалов. По-другому - экономические показатели стали неотделимыми от технических.
В начале XX века накопилось много фактов, не вкладывающихся в схему расчетов по рабочим состояниям. Вследствие изучения работы конструкций из пластических материалов при высоких нагрузках обнаружили, что поведение статически неопределимых конструкций из пластических материалов качественно изменяется после выхода из упругой области. Так, в изгибаемом элементе после проявления «текучести» линейное распределение напряжений переходит в нелинейное. В неразрезной балке или раме происходит перераспределение усилий таким образом, что при достижении предельного состояния конструкций превращается в статически определимую систему, которая имеет пластические шарниры в наиболее напряженных сечениях.
Особенно четко подобные факты и противоречия появились в связи применения нового комплексного материала - железобетона. Попытки использовать классическую теорию сопротивления материалов к расчету железобетонных конструкций даже в рабочем состоянии были неудачными. Возникновение трещин в растянутой зоне, проявление неупругих деформаций бетона, нарушение сцепления арматуры с бетоном не дали возможности правдиво оценивать напряженное состояние железобетона.
В строительной механике наступил кризис. Об этом знали все специалисты. Однако у каждого авторитета был свой путь преодоления противоречий между теорией и опытом.
В конце-концов сформулировались два основных направления.
Некоторые исследователи пошли путем расширения теоретических решений теории упругости в пластической области и это привело к созданию теории пластичности. Основой этого направления стал отказ от закона Гука и его замена более сложной зависимостью между напряжениями, деформациями и их изменением во времени. Главная цель этого направления - спрогнозировать поведение конструкции на всех этапах приложения нагрузки: от начального состояния к предельному, вплоть до разрушения. В этом направлении наиболее известны работы Надаи, Прагера, Мизеса, Генки, Ильюшина и др.
Следует отметить, что много решений теории пластичности требуют определения большого количества эмпирических характеров, а это значительно затрудняет применение предлагаемых решений.
Второй путь основан только на рассмотрении предельного состояния, без учета предыстории нагружения, что позволяет определять разрушающую нагрузку для той новой схемы, которую конструкция приобретает в предельном состоянии.
Такой подход является отрождением старого принципа по предельному состоянию, но с учетом точных сведений о поведении конструкции в рабочем состоянии, т.е. в упругой стадии. Через это выбор схемы разрушения осуществляется не произвольно, как раньше, а в сечениях с наибольшими внутренними усилиями в упругой стадии.
Пионером второго направления стал русский ученый А.Ф. Лолейт (литовец по происхождению), который в 1905г. сделал вывод о необходимости «рассматривать мгновенное равновесие непосредственно перед разрушением» как основную стадию расчета конструкции. Отметим, что Лолейт выразил это положение к железобетонным конструкциям, которые меньше всего вписывались в рамки классической теории.
Идея Лолейта получила признание не сразу - необходимо было четверть столетия, чтобы специалисты убедились в безрезультатности попыток оценивать железобетон с позиций теории упругости.
В это же время подобную идею относительно стальных конструкций высказал в 1926г. немец Грюнинг (Qruning). Дальнейшее развитие теории расчета металлических конструкций находит отражение в работах немецких исследователей Майера, Фриге, россиянина Н.С. Стрелецкого и др.
На основе работ А.Ф. Лолейта и А.А. Гвоздева, в бывшем СССР, была разработана стройная теория расчета по стадии разрушения, и в 1938г. эта методика была включена в нормы проектирования железобетонных конструкций.
В дальнейшем также развивается строительная механика упругих систем.
В последней четверти XIX века на примере одного из видов статически неопределимых систем (стальная ферма с жесткими узлами) получен расчет с использованием углов поворота в качестве основных неизвестных, т.е. по существу использован метод перемещений. В начале XX столетия за рубежом опубликовано ряд статей, посвященных расчету железобетонных рам при помощи этих самых неизвестных.
Большой вклад в развитие метода перемещений в 20-30х годах прошлого столетия внесли ученые бывшего Союза ССР: Н.А. Гвоздев, П.Л. Пастернак, Б.Н. Жемочкин, И.М. Рабинович, Б.Е. Бернштейн, Н.И. Безухов и др. Уравнения метода перемещений представлены в канонической форме и в развернутом виде. Даны способы упрощения уравнений и использования симметрии. Разработан комбинированный способ расчета рам. Методу перемещений, придано оконченную форму классического метода.
А.А. Гвоздев обобщал много методов расчета, в которых одна часть неизвестных представляет собой силы, а вторая часть - перемещения и представил их в общем виде под названием смешанного метода.
Широкую популярность приобрел предложенный А. Верещагиным способ перемножения эпюр при вычислении перемещений, хорошо известный каждому студенту технических учебных заведений.
В конце 30х годов XX века созрела необходимость пересмотра расчета для всех строительных конструкций, в том числе и для оснований и фундаментов. Поэтому в 1945г. при техническом совете Наркомстроя СССР под председательством В.М. Келдыша (отец будущего президента А Н СССР) была создана комиссия по выработке единого метода расчета строительных конструкций и совершенствованию коэффициентов запаса (позже комиссия перешла в подчинение Центрального научно-исследовательского института промышленных сооружений - ЦНИИПС). Она разработала новый универсальный метод расчета по предельным состояниям, установила эти состояния и дала им определение, заменила единый коэффициент запаса системой деференцированных коэффициентов. В 1949г. была опубликована итоговая работа комиссии - проект «Нормы проектирования конструкций. Материалы для Урочного положения», в которых приведен текст норм проектирования всех строительных конструкций и обоснования для отдельных разделов.
В дальнейшем на основании этих материалов были разработаны, утверждены и 21 января 1955г. введены в действие Строительные Нормы и Правила (СНиП), в которых расчет по предельным состояниям вводился в практику проектирования всех строительных конструкций. Количество предельных состояний в дальнейшем увеличивалось, но это не меняет принципиального подхода к расчету конструкций и фундаментов.
Основы расчета по предельным состояниям
Один из основоположников метода расчета по предельным состояниям Н.С. Стрелецкий дал такое определение предельного состояния: «Предельное состояние есть такое состояние конструкции, при котором ее эксплуатация должна быть прекращена».
В дальнейшем понятие предельного состояния видоизменялась, и теперь его формулируют следующим образом.
Предельное (предаварийное) состояние (здания) - состояние здания, его отдельных элементов, при котором их дальнейшая эксплуатация недопустима или восстановление их работоспособного состояния невозможно или нецелесообразно вследствие появления чрезмерных прогибов, трещин, локального или общего разрушения и других признаков ресурсного отказа (СНБ 1.04.01).
Количество предельных состояний изменялось в процессе изучения работы конструкций под нагрузкой, а также с учетом опыта их проектирования и эксплуатации.
При разработке метода расчета было установлено три предельных состояния конструкций:
- первое предельное состояние - по несущей способности;
- второе предельное состояние - по образованию или недопустимых деформаций;
- третье предельное состояние - по образованию или раскрытию трещин.
Такой трактат понятия предельных состояний был включен в первый в СССР общестроительный нормативный документ - Строительные нормы и правила 1954г. (Строительные нормы и правила. Госстрой СССР. - М.: Госстройиздат, 1954. - часть I: Строительные материалы, детали и конструкции. - 226с.; Часть II: Нормы строительного проектирования. - 404с.; Часть III: Правила производства и приемки строительных работ. - 208с.; Часть IV: Сметные нормы на строительные работы. - 450с.)
В дальнейшем происходит расширение и уточнение понятий предельных состояний. Современные стандарты установили две группы предельных состояний:
- первая группа включает предельные состояния, которые приводят к полной или частичной потери несущей способности зданий и сооружений в целом, а также полной непригодности к эксплуатации конструкций, фундаментов, зданий и сооружений в целом;
- вторая группа включает предельные состояния, затрудняющие нормальную эксплуатацию конструкций, оснований или уменьшают долговечность строений, сооружений сравнительно с предусмотрительным сроком эксплуатации.
Предельные состояния первой группы характеризуются:
- разрушением любого характера (хрупким, пластическим, усталостным);
- потерей устойчивости формы, приводящей к полной непригодности дальнейшей эксплуатации;
- потерей устойчивости положения;
- переходом к изменяемой системе;
- качественным изменением конфигурации;
- другими явлениями, при которых возникает необходимость прекращения эксплуатации (например, недопустимыми деформациями вследствие ползучести, пластичности, сдвига в соединениях, раскрытии трещин, а также возникновения трещин).
Предельные состояния второй группы характеризуются:
- достижением предельных деформаций конструкций (например, предельных прогибов, поворотов) или предельных деформаций оснований;
- достижением предельных уровней колебаний конструкций или оснований;
- образованием трещин;
- достижением предельного раскрытия или длины трещин;
- потерей устойчивости формы, приводящей к затруднению нормальной эксплуатации.
Суть расчета по предельным состояниям состоит в том, чтобы обеспечить надежность конструкций в течение всего срока службы, а также при выполнении строительно-монтажных работ. Обеспеченность надежности состоит в том, чтобы расчетные значения нагрузок или вызванные ими последствия (усилий, напряжений, деформаций, перемещений, раскрытие трещин) не превышали соответствующих им предельных значений, установленных нормами проектирования конструкций или фундаментов, т.е. необходимо удовлетворить требования вида
;
… (2.11)
;
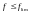… (2.12)
.
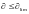… (2.13)
В этих формулах слева приведены усилия, напряжения, деформации и пр. вызванные внешними нагрузками; справа - соответствующие параметры несущей способности сечения конструкции или предельно допустимые деформации, перемещения и пр.
Расчет по предельным состояниям включает в себя и метод предельного равновесия, основное условие которого имеет вид
.
… (2.14)
т.е. внешняя нагрузка не должна превышать предельную (разрушающую нагрузку для рассматриваемой конструкции).
Нагрузки и воздействия
При расчете строительных конструкций одна из первоочередных задач - уточнить, что же может воздействовать на конструкцию, каким воздействиям она должна противостоять (сопротивляться). Все разнообразие воздействий принято подразделять на два вида: силовые (нагрузки) и не силовые (воздействия в узком понимании этого термина).
Нагрузка - 1. Механическое воздействие, мерой которого является сила, характеризующая величину и направление этого воздействия и вызывающая изменения напряженно-деформированного состояния конструкций зданий и сооружений и их оснований (СТБ 1900). 2. Механическое воздействие, мерой которого является сила, характеризующая численное значение и направление этого воздействия.
Воздействия - силы, приложенные непосредственно к конструкции и вызывающие в элементах конструкции напряжения, либо их перемещения, определяемые термином «воздействие непосредственное или прямое» или «нагрузка»; деформации элементов конструкций, вызванные перемещениями связи, соединяющих их с другими элементами, осадками оснований либо собственными деформациями (например, неравномерные осадки, усадка, ползучесть бетона, температурные изменения), вызывающими реактивные силы, которые определяют как «косвенные или непрямые воздействия» (СНБ 5.03.01).
На рис. 2.6 схематически представлены нагрузки и воздействия, которые могут воздействовать на многоэтажное здание.
В дальнейшем, когда это будет возможно словосочетание «нагрузки и воздействия» для удобства заменим термином «нагрузки».
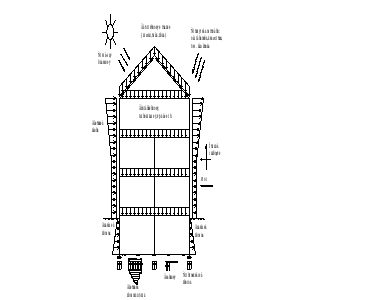
Рисунок 2.6 -Нагрузки и воздействия на здание
К нагрузкам относятся: собственный вес конструкции, вес оборудования, вес других частей зданий и сооружений, вес материалов, моделей, атмосферных осадков и пр.
К воздействиям относятся: температурные воздействия, которые вызывают удлинение или укорочение линейных размеров элементов, в этой связи в элементах и конструкциях возникает внутреннее напряженное состояние, а в помещениях возможна смена теплового режима;
действие атмосферной или тепловой влажности, а также парообразующей влаги (конденсация влаги с воздуха при резком перепаде температур), что может произвести к смене свойств материалов строительных конструкций или нарушить микроклимат в помещении, кроме этого, возможно снижение прочностных характеристик грунта основания;
проникновение внешнего воздуха внутрь посещений, что приведет к смене их режима влажности и теплового режима;
наличие в воздухе агрессивных химических веществ, что приводит к коррозии, особенно при наличии влаги;
биологические воздействия, вызванные насекомыми или микроорганизмами, что приводит к различным повреждениям конструкций органических материалов;
звуковые воздействия (шумы) от источников вне здания или сооружения, которые нарушают нормальную акустическую обстановку внутри строения или вызывают явление резонанса;
спонтанная деформация материалов (усадка, ползучесть), что вызывает «собственные» напряжения в элементах и конструкциях;
сейсмические воздействия, что вызывают резкие колебания грунтов вместе со зданиями и сооружениями;
явление деформации оснований, обусловленные коренным изменением структуры грунта (при замачивании просадочных грунтов) или оседанием грунта в районах горных выработок или в районах карстообразования;
вибрационные воздействия от родников, расположенных вне здания или сооружения.
Перечисленные воздействия существенно влияют на работу конструкций, потому их учитывают при расчете строительных конструкций совместно с нагрузками.
Параметры сопротивления материалов
Прочность любого сооружения зависит, прежде всего, от прочностных параметров использованных материалов. Одним из важных технических заданий является изучение прочностных особенностей материалов и определение их характеристик, используемых при расчете конструкций.
Прочностные характеристики материалов зависят от многих факторов: состава (химического, минералогического, гранулометрического и др.), технологии изготовления, однородности структуры, степени контроля качества, вида напряженного состояния, условий испытаний и др. Одновременно механические свойства материалов в той или иной мере изменяются даже при тщательном соблюдении одних и тех же условий изготовления и испытания.
Следует отметить, чтобы получить полную стабильность (неизменность) какого-нибудь свойства практически невозможно: при отработанной технологии изготовления уменьшение разброса свойств на 1-2 % приводит к существенному росту затрат - в несколько раз. Поэтому изменение свойств материалов можно рассматривать как совокупность случайных событий, к которым полностью применены методы математической статистики и теории вероятности. Эти методы широко используют при назначении нормируемых параметров, при оценке степени надежности расчетных характеристик и пр.
Дадим некоторые понятия, которые используются при статической обработке результатов испытаний или замеров.
В процессе изучения свойств материалов или при выборочном контроле на производстве получают совокупность опытных значений прочностного показателя R (границы текучести стали, кубиковой прочности бетона, временного сопротивления древесины и др.) с целью накопления информации о свойстве, которая изучается или контролируется. Для получения достоверной информации проводят сотни и тысячи испытаний длительное время. Полученную совокупность результатов подвергают статистической обработке.
Для
придания большей наглядности и
компактности материалы испытаний
первоначально обрабатывают - строят
так называемый статистический ряд. Для
этого весь диапазон конкретных результатов
разделяют на интервалы или «разряды»
и определяют количество значений,
которое припадает на каждый
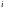-й
разряд.
Затем
складывают таблицу, в которой приводят
границы интервалов в порядке их
возрастания и соответствующее количество
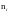результатов данного интервала. Такая
таблица получила название «статистический
ряд». Пример подобного статистического
ряда приведен в таблице 2.1.
Таблица 2.1