3. Расчет начальных условий
Если
схема n-го
порядка, то свободная составляющая тока
или напряжения содержит n
постоянных интегрирований, для определения
которых необходимо иметь n
начальных условий, соответственно, либо
значения тока и его производных до n-1
порядка в момент коммутации
,
либо значения напряжения и его производных
до n-1
порядка в момент коммутации
.
Начальные условия условно делят на две группы:
а) независимые начальные условия (ННУ),
б) зависимые начальные условия (ЗНУ).
Независимые
начальные условия - значение тока на
индуктивности и напряжение на ёмкости
в момент коммутации, т.е
и
.
Зависимые
начальные условия – значения токов
(кроме
)
и их производных любого порядка и
напряжений (кроме
)
и их производных любого порядка в момент
коммутации.
Расчет независимых начальных условий и .
Расчет
ННУ проводят на основе анализа режима
работы схемы (установившегося или
переходного) до коммутации, а именно:
рассчитывают
и
в соответствующем режиме по схеме до
коммутации и в полученные выражения
подставляют
(
в
выражениях для
и
означает,
что
и
– законы изменения соответственно тока
на индуктивности и напряжения на емкости
до коммутации,
–
момент коммутации). В результате получаем
значения
и
в момент времени, непосредственно
предшествующий коммутации, т.е
и
.
На основании законов коммутации
и
–
значение, соответственно, тока на
индуктивности и напряжение на емкости
в момент окончания коммутации (длительность
коммутации
).
Если учесть, что за начало отсчета времени принимают момент коммутации, то искомые НЗУ
Законы коммутации:
Ток на индуктивности
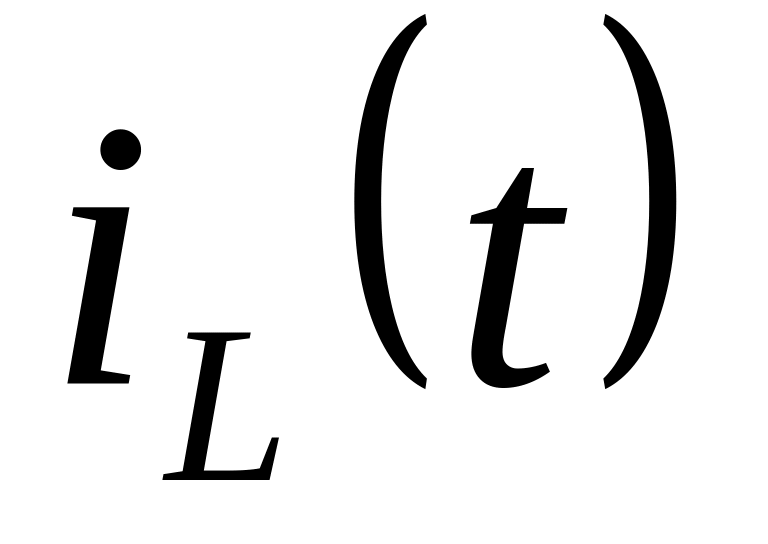– непрерывная функция,Напряжение на ёмкости
– непрерывная функция
или
для любого значения t.
б)Расчет зависимых начальных условий
либо
.
Процедуру расчета ЗНУ представим в виде некоторого циклического алгоритма.
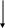
4. Расчет постоянных интегрирования
Записать выражения для искомого тока (напряжения) с учетом результатов, полученных на 1 и 2 этапах (значения принужденной составляющей и корней характеристического уравнения) и продифференцировать его последовательно n-1 раз. Подставить в эти n выражений t = 0 и значения найденных на 3 этапе начальных условий. В итоге получим систему уравнений относительно неизвестных постоянных интегрирования, позволяющую рассчитать их значение.
Задача 1
В
схеме рис.6 ключ коммутируется из
положения 1 в положение 2. До коммутации
в схеме установившейся режим. Параметры
схемы: R1=100
Ом, R2=300
Ом, R3=100
Ом, R4=200
Ом, L=25мГн,
C=0,1
мкФ, Е=200 В, J=0,4
А. Рассчитать
после коммутации ключа.
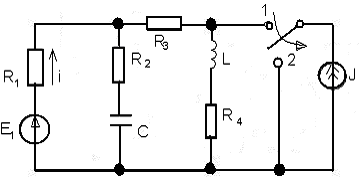
Рис. 6
Проведем расчет тока классическим методом в соответствии с методикой, изложенной в теоретических сведениях.
Расчет принужденной составляющей
В схеме действуют постоянные источники, поэтому через некоторое время после коммутации в схеме будет установившийся режим постоянного тока (УРПТ). Определим из анализа УРПТ после коммутации. Расчетная схема (схема установившегося режима постоянного тока после коммутации ключа) представлена на рис.7
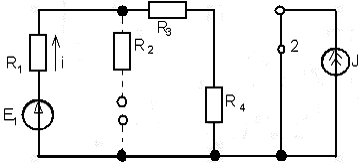
Рис. 7
Схема имеет такой вид, так как в УРПТ ток через емкость и напряжение на индуктивности равны нулю. Это утверждение отражают на эквивалентной схеме следующими заменами:
Тогда по ЗКН для схемы (рис.7) имеем
.
Составление характеристического уравнения и определение его корней.
Поскольку требуется рассчитать ток только в одной ветви, то для получения характеристического уравнения воспользуемся методом входного сопротивления. Для этого составим схему свободной составляющей и сделаем разрыв в той ветви, относительно тока которой требуется записать характеристическое уравнение (рис.8). Запишем выражение для входного (эквивалентного) сопротивления относительно зажимов разрыва.
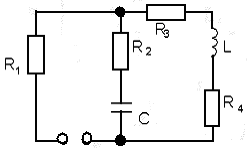
Рис. 8
.
Приравняем
выражение для
нулю
.
Это
уравнение является характеристическим
относительно тока
.
Подставив
значение параметров, и проведя необходимые
расчеты, получим
.
Определим корни этого уравнения
.
Так как p1=p2, т.е. корни кратные, то решение записывают в виде
,
A1 и A2 – постоянные интегрирования.
Расчет начальных условий
а) Расчет независимых начальных условий и . Рассмотрим режим работы схемы до коммутации. В схеме с постоянными источниками до коммутации установившийся режим, т.е. установившийся режим постоянного тока. В УРПТ коммутации схема имеет вид (рис.9)
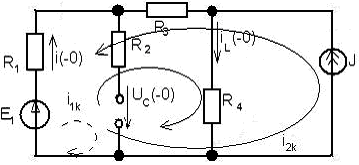
Рис. 9
Определим
методом контурных токов. Для указанных
контуров (рис.9) будем иметь
.
Учитывая,
что
получим
.
Или с учетом параметров схемы
.
Напряжение
рассчитаем по ЗКН, записанному для
пунктирного контура (рис 9)
.
Учитывая,
что
(в
ветви разрыв)
В соответствии с законами коммутации искомые независимые начальные условия
б) Расчет зависимых начальных условий
Выражение
тока
содержит
две постоянные интегрирования, для
определения этих постоянных интегрирования
необходимо иметь значения двух начальных
условий, а именно,
и
.
Зависимые начальные условия рассчитываются по схеме после коммутации (риc.10)
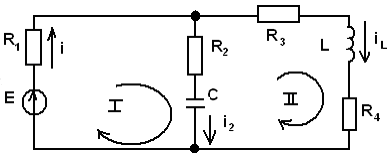
Рис. 10
Запишем для схемы (рис.10) полную системы независимых уравнений по ЗК
.
.
.
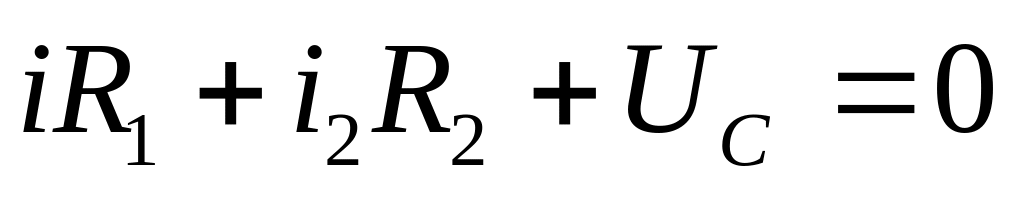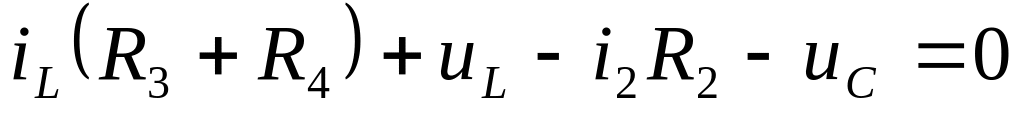Выразим
из первого уравнения
.
И подставим во второе
или
.
С учетом этого результата, записанную выше систему уравнений можно представить в следующем виде
(1.1)
(1.2)
. (1.3)
Эта
система уравнений (также как и предыдущая)
справедлива для любого
,
и используется для расчета начальных
условий.
Рассмотрим
уравнения 1.1 - 1.3 при
и определим
.
.
Определим
и
Продифференцируем уравнение (1.1)
.
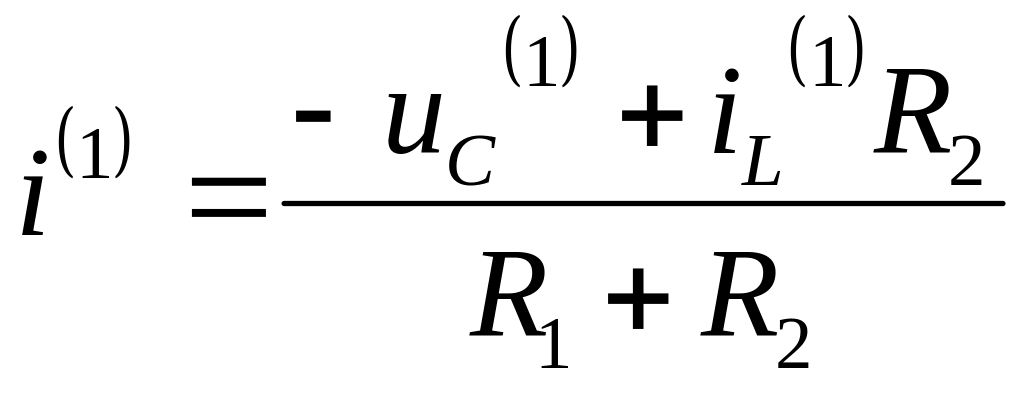И рассмотрим при t=0
.
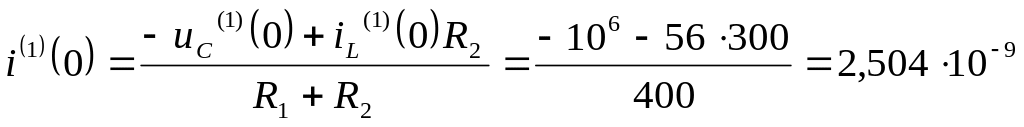Таким
образом необходимые начальные условия
определены.
4) Расчет постоянных интегрирования
Искомый ток в соответствии с результатами, полученными на I и II этапах расчета
.
Продифференцируем это выражение
И
подставим в выражение для
и
t=0
Тогда
.