Правительство Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Национальный исследовательский университет

«Высшая школа экономики»

Московский институт электроники и математики

Национального исследовательского университета

«Высшая школа экономики»

Кафедра электроники и наноэлектроники

АНАЛИЗ РЕЗИСТИВНЫХ СХЕМ НА ОСНОВЕ ЗАКОНОВ

КИРХГОФА И ОМА

Учебно-методическое пособие

по выполнению расчетно-графической работы

по дисциплине «Теоретические основы электротехники»

Москва 2013

Составитель проф., к.т.н. Е.Г. Осипов

Пособие содержит теоретические положения, необходимые для

выполнения расчетно-графических работ по курсу «Теоретические основы электротехники». Также приведены примеры расчета электрических схем.

УДК 621.3

Анализ резистивных схем на основе законов Кирхгофа и закона Ома: Учебно-метод. пособие по выполнению расчетно-графических работ по дисциплине «Теоретические основы электротехники» /

Московский институт электроники и математики Национального

исследовательского университета «Высшая школа экономики»;

Сост. Е.Г. Осипов. М., 2013. 10 с.

Ил. 4, библиогр. 4 назв.

ISBN 978-5-94506-311-2

Введение

Задачи анализа электрических цепей заключаются в следующем: известны конфигурация схемы замещения электрической цепи и параметры её элементов, а требуется определить токи, напряжения и мощности тех или иных участков. В данной разработке представлено применение основных методов анализа резистивных схем.

Резистивная схема – это схема, содержащая следующие элементы: сопротивления R, источники ЭДС и источники тока .

R

e

j

Произвольная схема имеет B ветвей и У узлов. Будем исходить из того, что известна конфигурация схемы и известны параметры её элементов, т.е заданы значения всех R, и и необходимо рассчитать токи во всех ветвях и напряжения на источниках тока. Суммарное количество неизвестных равно числу ветвей: (В - В_i) – количество неизвестных токов ветвей и B_i - количество неизвестных напряжений на источниках тока (B_i – число ветвей с источниками тока).

Таким образом, для решения поставленной задачи необходимо иметь не менее B уравнений. Трудоемкость расчета в первую очередь зависит не от общего числа уравнений, а от количества совместно решаемых уравнений. Поэтому для расчета каждой конкретной схемы следует выбирать тот метод, при котором количество совместно решаемых уравнений будет минимальным, хотя общее количество используемых уравнений может превышать число ветвей.

Расчет резистивных схем по законам Кирхгофа. Закон Кирхгофа токов (зкт)

Алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю. При этом токи, направленные к узлу, учитывают с одним знаком, а от узла – с противоположным.

i₂

i₁

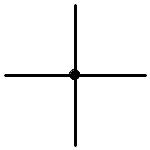
и ли

i₃

i₄

В первом уравнении токи, направленные к узлу, учтены со знаком плюс, а от узла – со знаком минус. Во втором уравнении наоборот: токи, направленные к узлу, со знаком минус, а от узла – со знаком плюс. По закону Кирхгофа токов можно составить К_ЗКТ =У-1 независимых уравнений.

Закон Кирхгофа напряжений (зкн)

Алгебраическая сумма напряжений на всех элементах контура, кроме источников ЭДС, равна алгебраической сумме ЭДС этого контура. В левой части уравнения учитывают напряжения на сопротивлениях i*R и источниках тока U_j со знаком плюс, если произвольно выбранное направление обхода контура совпадает соответственно с направлением тока на сопротивлении и направлением напряжения на источнике тока. В противном случае – со знаком минус. В правой части уравнения ЭДС учитывают со знаком плюс, если направление обхода контура совпадает с направлением ЭДС, и со знаком минус, если эти направления противоположны.

R₂

R₄

R₅

R₁

e₂

e₄

e₁

j₃

j₅

i₁

i₂

i₄

u_j3

u_j5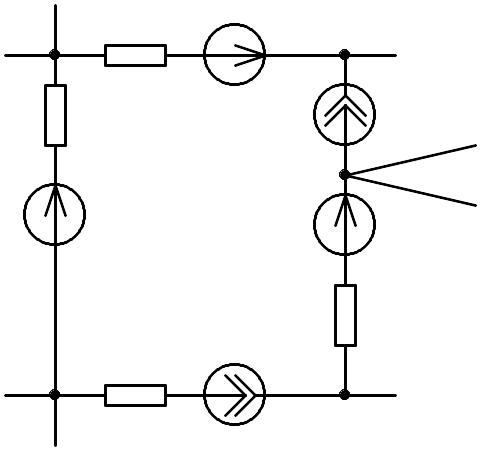

Рис. 1

По ЗКН можно записать К_ЗКН = В – (У-1) независимых уравнений.

Основные этапы расчета резистивных схем по законам Кирхгофа

1. Произвольно задать положительные направления токов во всех ветвях и напряжений на источниках тока.

2. Выбрать совокупность независимых контуров и задать произвольно направления обхода в этих контурах. Количество независимых контуров определяют по выражению К_НК = В – (У-1) , где В – количество ветвей,

У- количество узлов.

Рекомендации: а) Если схема содержит ветви с источниками тока, то контуры следует выбирать таким образом, чтобы каждая ветвь с источником тока входила в состав только одного контура и была единственной ветвью с источником тока в этом контуре. б) Если возникают трудности с выбором совокупности независимых контуров, то следует построить дерево графа схемы, при этом к ветвям связи следует отнести все ветви с источниками тока. Поочерёдно восстанавливая по одной ветви связи, получают полную совокупность независимых контуров.

3. Записать для любых У-1 узлов уравнения по ЗКТ и для выбранной совокупности независимых контуров уравнения по ЗКН. К_ЗКН = В-(У-1).

4. Решить систему уравнений п.3 относительно неизвестных токов ветвей и напряжений на источниках тока. Примечание. Рекомендация а) п.2 позволяет систему из В уравнений, составленных по ЗК, разбить на систему из В – В_i совместно решаемых уравнений относительно неизвестных токов, и В_i отдельных уравнений относительно напряжений на источниках тока.

R₁

R₂

R₃

R₄

e₁

e₄

e₃

i₁

(1)

(2)

(3)

(4)

I

II

III

e₆

е₄

R₅

e₅

е₄

R₆

R₄

i₄

i₅

i₆

Задача 1 Рассчитать токи во всех ветвях, если известны параметры схемы, т.е заданы значения всех и R.

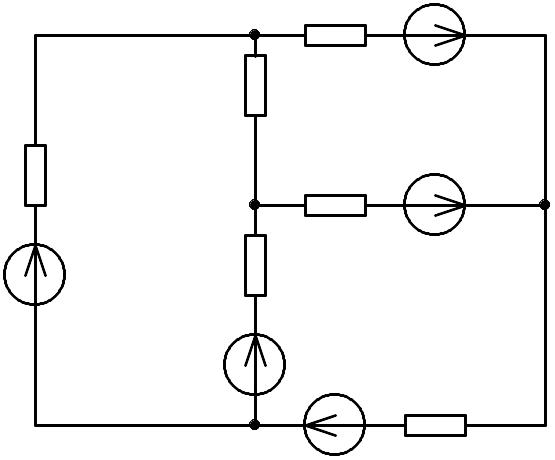
Рис. 2

i₂

i₃