2. Означення скалярного добутку

Скалярним добутком двох векторів називається число, що дорівнює добутку довжин цих векторів на косинус кута між ними:

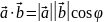
Скалярний добуток двох векторів, заданих координатами в прямокутній системі координат, дорівнює сумі добутків їхніх відповідних координат:

Геометричний зміст скалярного добутку: скалярний добуток двох векторів дорівнює добутку довжини одного вектора на проекцію на нього другого вектора.

Механічний зміст скалярного добутку: робота дорівнює скалярному добутку вектора сили на вектор переміщення.

3. Властивості скалярного добутку

Алгебраїчні властивості скалярного добутку:

1. (комутативність)

2. (дистрибутивність)

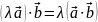3. (асоціативність)

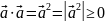4. скалярний квадрат вектора

( тільки при )

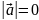Геометричні властивості скалярного добутку:

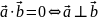1. (умова перпендикулярності векторів)

2. ( – гострий кут)

3. ( – тупий кут)

4. Кут між векторами

Кут між векторами та визначається рівністю

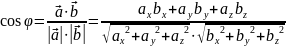
Необхідною і достатньою умовою перпендикулярності двох векторів є нульовий скалярний добуток цих векторів, тобто

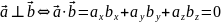
Проекція вектора на вектор :

Приклади.

1. При якому значенні 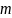вектори 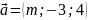та взаємно перпендикулярні?

Розв'язання. Користуючись скалярним добутком двох векторів утворюємо рівність:

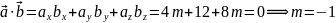
Відповідь. При

2. Дано вершини трикутника . Визначити його внутрішній кут при вершині .

Розв'язання. Знайдемо вектори та їх довжини, а потім і кут між ними:

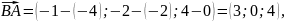
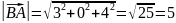
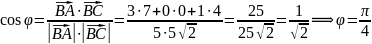
Відповідь.

3. Знайти 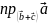, якщо

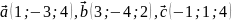
Розв'язання.

Відповідь.

Завдання для самоконтролю.

1. Як визначаються координати і довжина вектора в прямокутній декартовій системі координат?

2. Як знайти відстань між точками, заданими певними координатами?

3. Що називається напрямними косинусами вектора? Як їх знайти?

4. Як здійснюються лінійні операції над векторами, заданими певними координатами?

5. Які координати матиме точка, що ділить відрізок у деякому відношенні ?

6. Що називається скалярним добутком двох векторів?

7. У чому полягає геометричний та механічний зміст скалярного добутку?

8. Сформулюйте властивості скалярного добутку.

9. Яке взаємне розташування векторів, якщо їхній скалярний добуток дорівнює нулю?

10. Відомо, що 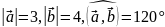. Обчисліть:

    1. ;

    2. ;

    3. ;

    4. 

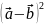11. Відомо, що . Знайдіть 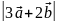та .

12. Відрізок поділено точками 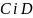на три рівні частини. Знайдіть координати точок поділу, якщо відомі координати кінців відрізка і .

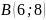13. В точках і містяться маси і 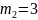. Знайдіть центр мас вказаних точок.

14. Знайдіть , якщо .

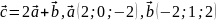15. Трикутник заданий вершинами 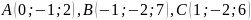. Знайдіть внутрішні кути трикутника.

16. Знайти кут між діагоналями паралелограма, побудованого на векторах .

ЗМ 11 Векторний добуток векторів