Формули переходу від полярних координат до декартових:

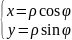
Формули переходу від декартових координат до полярних:

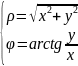
Приклад. Побудувати точки у полярній системі координат за такими даними:

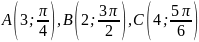
4. Циліндрична система координат

Якщо в прямокутній системі координат замість перших двох координат 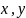взяти полярні координати , а третю координату лишити без зміни, то дістанемо циліндричну систему координат.

Координати точки простору в цій системі записують: .

Якщо прямокутну і циліндричну системи координат сумістити так, щоб їх початки координат і осі 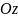збігались, то можна встановити залежності між цими системами:

5. Сферична система координат

У прямокутній системі координат візьмемо точку і проведемо через цю точку та вісь площину. Тоді – відстань від початку координат до даної точки ; – двогранний кут між площинами та ; – кут між віссю і променем . Упорядкована трійка чисел 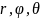однозначно визначає положення точки у просторі і носить назву сферичних координат точки .

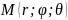Якщо розмістити прямокутну і сферичну системи координат таким чином, щоб початки координат збігалися, то можна встановити залежності між координатами:

6. Поняття про n-вимірний простір

Між геометричними векторами і їхніми координатами у фіксованому базисі існує взаємно однозначна відповідність. При цьому кожному вектору простору співставляється упорядкована трійка чисел, кожному вектору, що належить деякій площині, – упорядкована пара чисел, а кожному вектору на прямій – дійсне число, і навпаки.

Упорядковану трійку чисел називають тривимірним вектором, а множину всіх тривимірних векторів називають тривимірним простором (R³).

Упорядковані пари чисел називають двовимірними векторами, а числа – одновимірними. Множини двовимірних і одновимірних векторів називають відповідно двовимірними (R²) і одновимірними (R¹) просторами.

Узагальнюючи простори R¹, R², R³ приходимо до n-вимірного простору Rⁿ, де 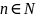(довільне натуральне число).

Упорядкована множина n дійсних чисел 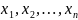називається n-вимірним вектором 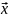і позначається .

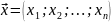Множина всіх n-вимірних векторів називається n-вимірним простором (Rⁿ). Якщо довільний вектор простору Rⁿ розглядати як радіус-вектор відповідної точки відносно початку координат обраної системи, то координати точки визначаються як координати цього радіуса-вектора.

Простори R¹, R², R³ є окремими випадками простору Rⁿ. Геометрично зображають лише одно-, дво- та тривимірний простори; для 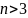простори Rⁿ уявити не можна, проте вони відіграють важливу роль у науці і техніці.

Приклад.

1. Розв'язок системи рівнянь з n невідомими є n-вимірним вектором.

2. Кожний рядок матриці 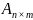є n-вимірним вектором, а кожний стовпець – m-вимірним. Рядки називають горизонтальними, а стовпці – вертикальними векторами матриці. Отже, довільну матрицю можна розглядати як деяку упорядковану сукупність її вертикальних або горизонтальних векторів.