2. Прямокутна система координат

Очевидно, що декартових систем координат можна задати скільки завгодно. Серед них широко використовується прямокутна декартова система координат.

Ортонормованим базисом називається упорядкована трійка одиничних попарно ортогональних векторів. Позначають ортонормований базис через вектори 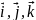, де .

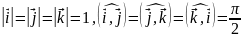У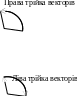 порядкована трійка векторів не компланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого вектора видно проти годинникової стрілки; в протилежному випадку трійка векторів називається лівою.

Прямокутною декартовою системою координат називається декартова система координат, базис якої ортонормований. Прямокутна система координат називається правою (лівою), якщо її ортонормований базис утворює праву (ліву( трійку векторів. Надалі користуватимемось правою системою координат, яка визначається правим ортонормованим базисом: .

Прямокутну систему координат позначають через ( 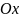– вісь абсцис, 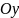– вісь ординат, 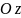– вісь аплікат), а координатні площини – через 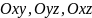. Вони поділяють простір на вісім октантів. При зображенні системи координат, як правило, показують лише осі координат, вектори не вказують.

Радіус-вектор точки записують у вигляді:

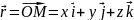або

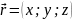
Координати радіус-вектора є координатами відповідної точки, які записують так: .

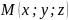З ортогональності базисних векторів системи випливає, що координати точки дорівнюють відповідним проекціям радуса-вектора цієї точки на відповідні осі координат:

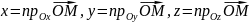
Прямокутні координати точки на площині і на прямій визначаються аналогічно як і в просторі.

Прямокутна система координат 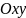на площині задається точкою – початком координат і двома взаємно перпендикулярними одиничними векторами 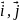– базисом системи координат. Точка на площині має лише дві координати – абсцису і ординату – 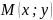. Система координат на прямій задається точкою і одиничним вектором 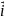, а точка має відповідно одну координату – абсцису – .

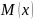Приклади.

1. На координатній прямій побудувати точки і

2. У прямокутній системі координат побудувати точки .

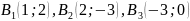3. У прямокутній системі координат побудувати точки .

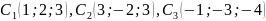Розв'язання.

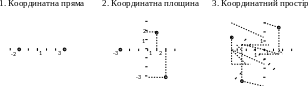
3. Полярна система координат

Декартова система координат не єдиний спосіб визначати за допомогою чисел місце знаходження точки на площині.

Полярна система координат задається точкою – полюсом та променем 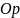, який виходить з полюса і називається полярною віссю. Задаються також одиниці масштабу: лінійна – для вимірювання довжин відрізків і кутова – для вимірювання кутів.

Довільна точка на площині у полярній системі координат матиме полярний радіус – відстань від точки до точки (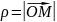 ) та полярний кут – кут, на який треба повернути полярну вісь проти годинникової стрілки, щоб сумістити її з вектором ( ).

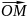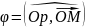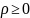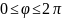П олярний радіус може набувати довільних невід'ємних значень , а полярний кут вважатимемо таким, що змінюється в межах . Іноді розглядають і більші кути, а також від'ємні кути, тобто ті, що відкладаються від полярної осі за годинниковою стрілкою.

Координати точки записують так: .
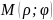