4. Интерполирование сплайнами

С увеличением числа узлов интерполирования растет степень полинома, что приводит к росту объема вычислений, а чтобы оценка погрешности (20) была конструктивной, требуется высокая гладкость приближаемой функции. Поэтому в середине прошлого века весьма плодотворной оказалась идея использовать кусочно-полиномиальную интерполяцию при помощи полиномов третьей степени, так называемых кубических сплайнов.

Пусть на отрезке выбрано некоторое множество узлов

, (25)

в которых заданы значения функции .

Определение.

Кубическим сплайном функции на сетке (25) называется дважды непрерывно-дифференцируемая функция , удовлетворяющая условиям:

45

1. На каждом отрезке функция является полиномом третьей степени.

2. .

3. .

Замечание. Последнее условие может быть иным, например

.

Перейдем к построению такого сплайна. Для простоты изложения, рассмотрим случай постоянной сетки :

.

На отдельном отрезке в записи искомого полинома третьей степени содержится четыре неизвестных коэффициента. Всего неизвестных , для нахождения которых имеется условий:

(26)

(27)

(28)

Способы нахождения этих коэффициентов и конкретный вид полинома могут быть различными. Рассмотрим один из них.

Пусть

(29)

Так как - линейная на отрезке функция, то ее вид определяется значениями и :

46

. (30)

Очевидно, что условия (28) при этом выполнены. Интегрируя (30) дважды по , получаем

,

где - произвольная линейная функция, которую можно выбрать в удобном для нас виде:

.

Тогда

. (31)

Выполнение условий (26) приводят к соотношениям:

,

откуда

.

Следовательно

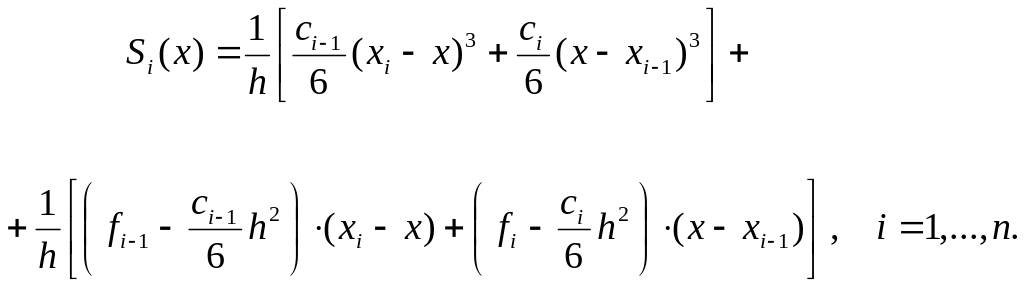(32)

47

Чтобы получить систему уравнений для нахождения , продифференцируем (32). Тогда

. (33)

Подставляя (33) в (27) , получаем

Откуда

(34)

Соотношения (34) представляют собой систему линейных алгебраических уравнений, матрица которой имеет диагональное преобладание, поэтому существует единственное решение (34), которое можно найти методом прогонки.

Замечание. Точность интерполирования с помощью сплайнов можно получить из следующей теоремы, которую приведем без доказательства.

Теорема. Пусть имеет на сегменте четыре непрерывных производных и удовлетворяет условию . Тогда для любого справедливы оценки:

(35)

(36)

(37)

(38)

48