Из (11) и (15) следует

,

откуда

,

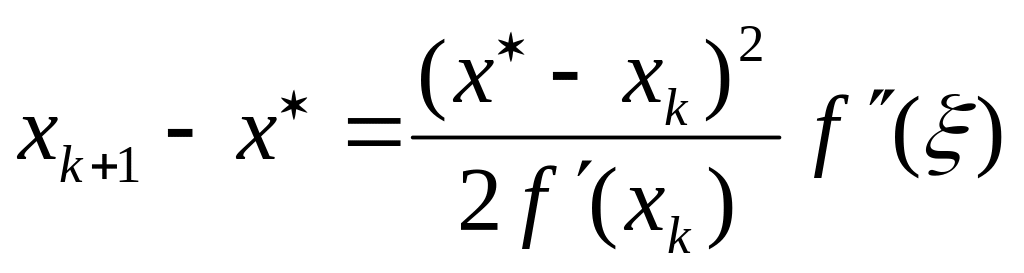. (16)

Далее

.

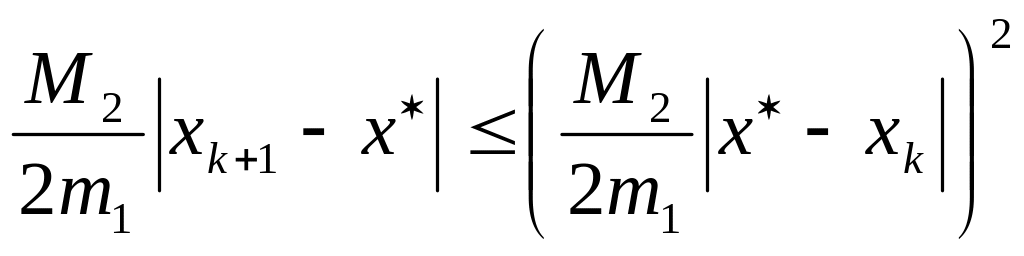Обозначим

,

тогда

.

Следовательно

,

и

. (17)

Что и завершает доказательство теоремы.

Таким образом доказано, что метод Ньютона имеет квадратичную сходимость, а это гораздо лучше, чем в методе простой итерации. К недостаткам метода можно отнести тот факт, что начальное приближение выбирается при довольно жестких ограничениях (13).

36

В заключении заметим, без доказательства, что в случае кратного корня , метод Ньютона не дает квадратичную сходимость. Поэтому для увеличения скорости сходимости применяют модифицированный метод Ньютона

, (18)

здесь - кратность корня.

В качестве примера рассмотрим уравнение (1) с функцией

.

Итерационный процесс (12) принимает вид

,

и сходится только в случае .

Модифицированный метод (18) с

, (19)

что эквивалентно применению метода Ньютона для нахождения

при и .

Упражнение для самостоятельного решения.

Выписать формулу метода Ньютона для нахождения значения , не используя операции деления.

37

Глава III

Интерполирование и приближение

Функций

Пусть нам известна некоторая информация о функции , определенной на отрезке .

Требуется, используя эту информацию , заменить (приблизить) функцию другой функцией , близкой к и более удобной для дальнейших исследований. Степень информированности может быть различной. Например:

а) задана на всем отрезке формулой, выражающей через элементарные функции (полная информированность),

б) является решением некоторого уравнения, найти точное решение которого не представляется возможным,

в) информация относительно функции известна только в некоторых точках отрезка.

Способ построения функции определяется как степенью информированности, так и свойствами, которыми должна обладать , чтобы быть пригодной для дальнейших исследований.

§1. Интерполирование функций.

Пусть в точках известны значения и может быть значения производных. Способ построения , используя информацию о значениях в отдельных точках , называется интерполированием. Рассмотрим несколько вариантов

нахождения функции .

1. Интерполяционные полиномы Лагранжа и Ньютона.

Будем искать функцию в виде полинома степени

(1)

38

Коэффициенты находятся из условий

(2)

Или в развернутом виде

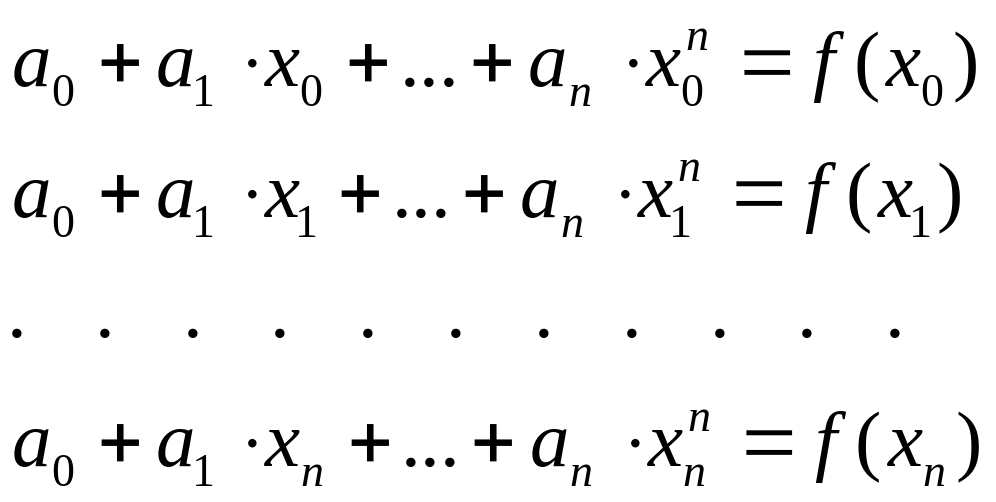(3)

Определителем этой системы линейных алгебраических уравнений является определитель Вандер-Монда, который в случае различных узлов интерполирования отличен от нуля.

Поэтому система (3) всегда имеет единственное решение и следовательно существует интерполяционный полином (1) .

Находить решение этой системы при больших весьма затруднительно, поэтому получим явное представление полинома не решая систему (3) напрямую.

А. Интерполяционный полином в форме Лагранжа.

Представим искомый полином в виде

, (4)

где полиномы степени , удовлетворяющие условиям

,

. (5)

Поэтому

. (6)

39

b. Интерполяционный полином в форме Ньютона.

Для построения интерполяционного полинома Ньютона нам понадобится понятие разделенной разности.

Пусть в различных точках , известны значения функции . Разделенные разности нулевого порядка

есть значения функции ; разделенные разности первого порядка определяются равенствами

, (7)

разделенные разности второго порядка равенствами

, (8)

и в общем случае разности -го порядка определяются через разности -го порядка по формулам

. (9)

Имеет место равенство

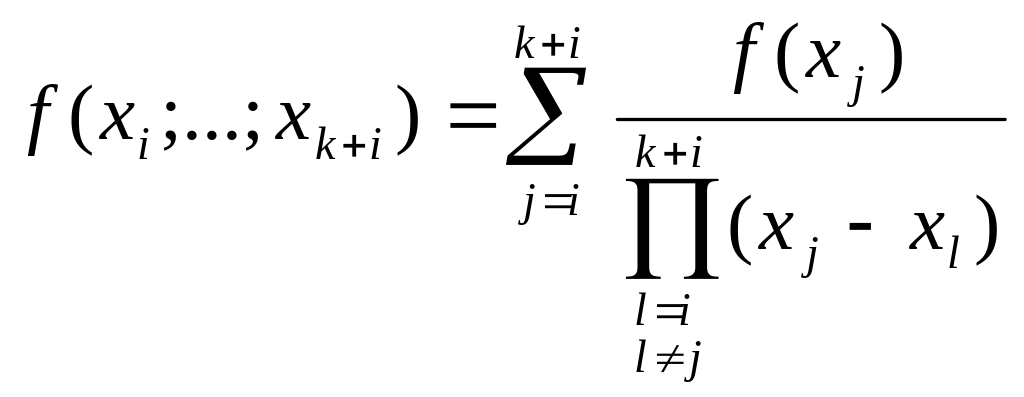. (10)

Доказательство проведем по индукции. При равенство верно исходя из определения (7). Пусть формула (10) верна при . Тогда

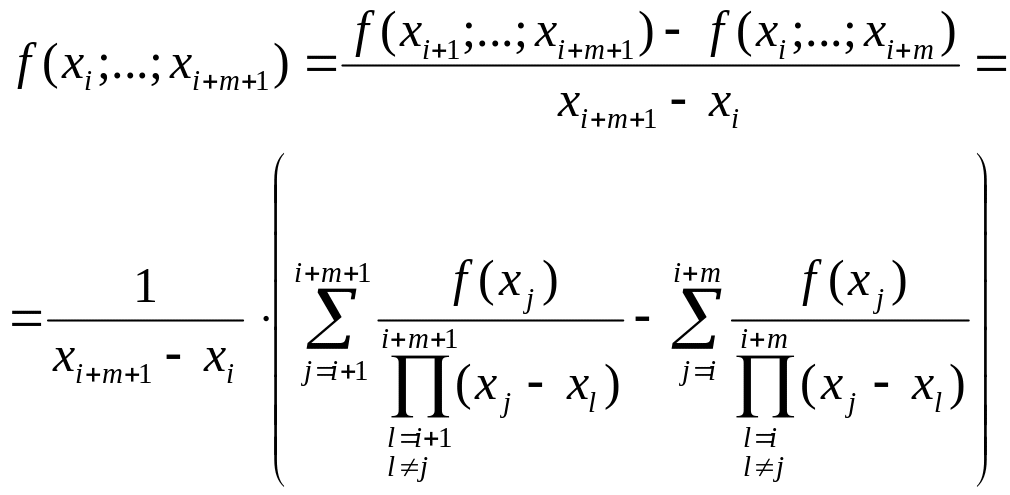(11)

40

В равенстве (11) слагаемые содержащие и встречаются только по одному разу, причем с коэффициентами имеющими требуемый вид. Остальные встречаются дважды, и коэффициент при равен

,

что и требовалось доказать.

Перейдем к выводу формулы полинома Ньютона, Для этого перепишем интерполяционный полином Лагранжа в виде:

, (12)

здесь интерполяционный полином Лагранжа по узлам и . Полином

(13)

имеет степень и обращается в нуль в точках , поэтому его можно представить в виде

, (14)

где коэффициент при в полиноме .

Из (6) и (10) следует, что

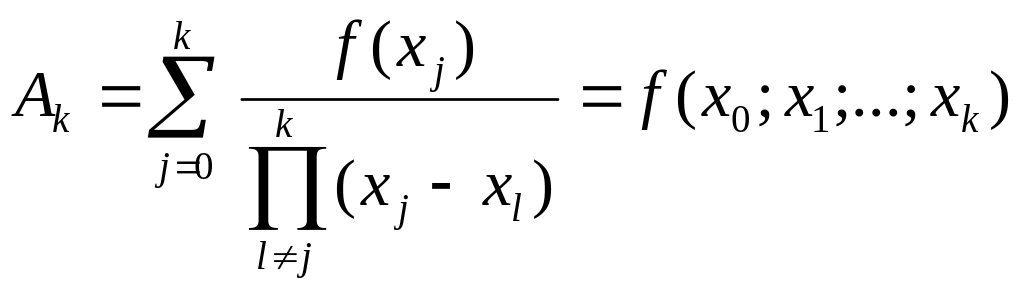. (15)

41

Учитывая (12)–(15), получаем

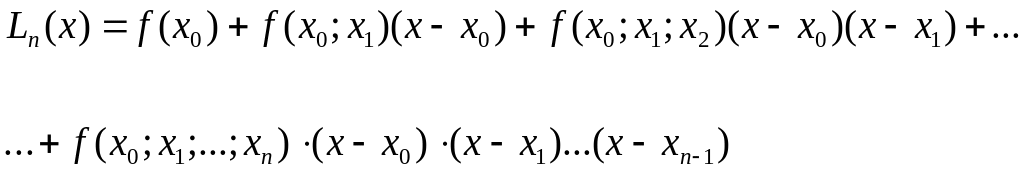. (16)

Интерполяционный полином, записанный в виде (16) принято называть интерполяционным полиномом Ньютона.

Отметим, что в силу единственности решения системы (3), полиномы Лагранжа и Ньютона представляют собой различные формы записи одного и того же интерполяционного полинома.