В.П. Заярный, А.Н. Шилин, А.И. Нефедьев

АНАЛОГОВАЯ ЭЛЕКТРОНИКА

Учебное пособие

Волгоград

2007

УДК 681.32

Рецензенты:

д – р техн. наук, профессор В.П. Шевчук

канд. техн. наук, доцент А.М. Чмутин

Заярный В.П., Шилин А.Н., Нефедьев А.И.

Аналоговая электроника: Учебное пособие / – Волгоград: Изд-во ВолгГТУ, 2007. – с.

Данное учебное пособие содержит необходимый теоретический материал для проведения базовых лабораторных работ или лабораторного практикума по темам: пассивные линейные и нелинейные элементы электрических цепей, управляемые активные элементы электрических цепей, их характеристики. Студентам на примерах предлагается произвести элементарный расчет электрических и электронных схем. Предлагается произвести сравнение расчетных характеристик схем с результатами, полученными в процессе эксперимента. В пособии также приведены необходимые разъяснения по выполнению каждой лабораторной работы, контрольные вопросы и список рекомендуемой литературы для углубленной проработки материала.

Пособие предназначено для студентов высших технических учебных заведений, изучающих курсы «Электроника», «Электротехника и электроника», «Аналоговая электроника» и других профильных дисциплин, а также для выполнения практикума.

Предисловие

Цель настоящего учебного пособия – способствовать углубленному получению знаний студентами по профильным дисциплинам, изучаемым в высших учебных заведениях для всех форм обучения.

Предлагаемый учебный материал содержит теоретическую часть и цикл лабораторных работ (всего 12 работ) предполагает знакомство студентов со свойствами, характеристиками и практическим применением пассивных элементов электрических цепей (как линейных, так и нелинейных) и активных элементов электрических цепей, начиная с простейших. В соответствии с этим, данное учебное пособие состоит из четырех разделов, содержащих теоретический материал, необходимый для выполнения предлагаемых лабораторных работ, описания каждой лабораторной работы, порядка ее выполнения и обработки полученных результатов. Для каждой лабораторной работы имеется список контрольных вопросов.

В предлагаемом теоретическом материале (по разделам) даны необходимые определения и понятия с интерпретацией, приведены необходимые соотношения (формулы) и к ним даны соответствующие пояснения.

Для углубленной проработки материала студентам в каждом разделе приводится список рекомендуемой литературы, что поможет им эффективнее и с большей пользой проработать материал, необходимый для грамотного выполнения соответствующих лабораторных работ.

В предлагаемом цикле лабораторных работ имеется материал повышенного объема и повышенной сложности. Это дает возможность изучать его в разных объемах, как в рамках необходимого минимума при выполнении лабораторных работ, так и в процессе прохождения студентами производственной практики.

Авторы

1. RC-цепи, их свойства

1.1. Теоретическая часть

1.1.1. Переходные процессы в цепи, состоящей из емкости и сопротивления

Подключим незаряженный конденсатор, емкостью , через резистор, сопротивлением к источнику питания с постоянным напряжением (ключ находится в положении 1), см. рис. 1.

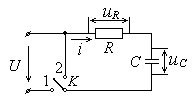
Рис. 1. Последовательная RC-цепь

Известно, что напряжение на зажимах конденсатора пропорционально заряду на его пластинах . Если конденсатор не заряжен, то напряжение на нем в момент подключения к источнику напряжения, равно нулю (на рис. 1 ключ К переводится в положение 1). То есть . Далее конденсатор начинает заряжаться. После окончания заряда (достижение установившегося режима) напряжение на нем равно напряжению источника питания, то есть .

Во время заряда конденсатора напряжение на нем равно сумме двух составляющих: напряжения принужденного режима и напряжения свободного режима т.е.

(1)

Используя второй закон Кирхгофа, запишем:

.

Так как ток , то уравнение данной цепи будет иметь вид:

(2)

С учетом (1) и (2), можно записать:

(3)

Из последнего уравнения для свободного режима получаем:

.

Величина называется постоянной времени цепи (имеет размерность времени). Чем больше , тем медленнее процесс и наоборот. Следовательно, . Интегрируя уравнение почленно, найдем

,

откуда

.

Постоянную интегрирования определим из начальных условий. При , согласно второму закону коммутации, . Тогда , откуда или .

Таким образом, в процессе заряда конденсатора напряжение на нем изменяется по закону:

. (4)

Ток переходного режима, или зарядный ток будет определяться выражением:

. (5)

Падение напряжения на сопротивлении будет изменяться пропорционально току:

(6)

Из формул (4), (5) и (6) видно, что при ток заряда и напряжение стремятся к нулю, а напряжение – к значению напряжения . За время, равное одной постоянной времени цепи , конденсатор зарядится только до величины (при этом зарядный ток уменьшится в раза). Практически считают, что конденсатор зарядился и переходный процесс закончился, если напряжение на нем достигло значения . Это произойдет через время, равное трем постоянным времени цепи: .

Если после заряда конденсатора (в момент времени , рис. 2) перевести ключ в положение 2 (рис. 1), то заряженный конденсатор окажется замкнутым на резистор , а в цепи начнет протекать ток разряда конденсатора . Напряжение на зажимах цепи также, как и в предыдущем случае, равно сумме напряжений на емкости и на сопротивлении , то есть:

.

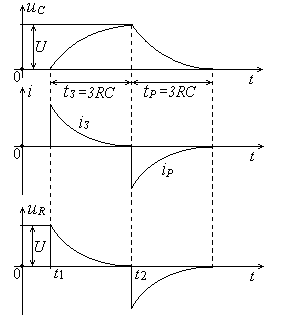
Рис. 2. Диаграмма напряжений и тока в RC-цепи

Но, так как в этом случае в цепи нет источника питания, то будут иметь место равенства:

, и , .

Согласно второму закону Кирхгофа, уравнение цепи будет иметь вид: , или ,

а ток в цепи

(7)

Знак минус показывает, что при разряде конденсатора ток в цепи направлен обратно тому положительному направлению, которое показано на рис. 1, и обратно току заряда конденсатора .

Так как ток , то уравнение цепи, с учетом (7), примет вид:

,

откуда получаем дифференциальное уравнение для напряжения на конденсаторе:

.

Интегрируя правую и левую части уравнения, получим:

.

Из этого выражения следует, что

. (8)

Постоянную также найдем из начальных условий. Согласно второму закону коммутации в начальный момент времени разряда конденсатора напряжение остается таким же, как до переключения ключа , т.е. , и, в соответствии с (8), . Следовательно .

Таким образом, напряжение на конденсаторе при его разряде: , (9)

а разрядный ток в цепи:

. (10)

Напряжение на конденсаторе в начальный момент времени разряда ( ) имеет наибольшее значение, а затем изменяется по закону показательной функции, достигая по прошествии времени практически нулевого значения (0,05 первоначального напряжения на нем). Ток в контуре в момент скачком изменяется от нуля до значения , а затем изменяется пропорционально напряжению на конденсаторе. Скорость протекания процесса, как и в предыдущем случае, определяется постоянной времени . Данные рассуждения поясняются временными диаграммами напряжения и тока, приведенными на рис. 2.