29

Лекція 1 Системи випадкових величин

Системою випадкових величин X,Y,Z,…(1) називають набір випадкових величин (1), які характеризують векторну випадкову величину (X,Y,Z,…W). Наприклад, точка попадання снаряда визначається не однією випадковою величиною X, але ще і випадковою величиною Y; точка розриву дистанційного снаряду визначається трьома випадковими величинами X,Y,Z. При стрільбі групою із n пострілів сукупність точок попадання на площині може розглядатись як система 2n випадкових величин. Властивості системи декількох випадкових величин не вичерпуються властивостями випадкових величин, які входять до неї; вони ще включають також взаємні зв’язки між випадковими величинами. Геометрично систему двох випадкових величин X,Y зручно представити випадковою точкою на площині XOY. Систему n випадкових величин можна представити як випадкову точку в просторі n-вимірному. Часто замість образу випадкової точки для геометричної інтерпретації системи випадкових величин користуються образом випадкового вектора.

y

Y

Функція розподілу системи двох випадкових величин

Функцією розподілу системи двох випадкових величин (X,Y) називається ймовірність сумісного виконання двох нерівностей X<x i Y<y:

F(x,y)=Q((X<x)(Y<y)) (2)

Г еометрично F(x,y) є не що інше, як ймовірність попадання випадкової точки (X,Y) в нескінченний квадрант з вершиною в точці (x,y), який лежить зліва і нижче цієї точки.

Г еометрично F₁(x) i F₂(y) є:

X

Властивості F(x,y):

1. Функція розподілу F(x,y) є неспадна для обох своїх аргументів, тобто при x₂>x₁, F(x₂,y) ≥ F(x₁,y)

при y₂>y₁, F(x,y₂) ≥ F(x,y₁)

(з властивостей ймовірностей, а також з геометричної інтерпретації).

2. F(x,-∞)=F(-∞,y)=F(-∞,-∞)=0

(геометрично та з властивостей ймовірності)

3. F(x,+ ∞)= F₁(x)

F(+∞,y)=F₂(y), де F₁(x), F₂(y) – відповідно функції розподілу випадкових величин X i Y.

(геометрично та з властивостей ймовірності)

4. F(+∞,+∞)=1

( геометрично та з властивостей ймовірності) \

Знайти Q((x,y) D) ?

Якщо D є прямокутна область R, то

Q((x,y) є R)=Q(α≤X<ß)( γ ≤Y<δ)))= F(ß,δ)-F(α,δ)-F(ß,γ)+F(α,γ) (3)

Пізніше одержимо формулу через щільність розподілу системи двох випадкових величин.

Щільність розподілу системи двох випадкових величин

Розглянемо на площині XOY прямокутник R_Δ з сторонами Δx I Δy, який дотикається до точки з координатами (x,y)

y

x

x

Ймовірність попадання в цей прямокутник за формулою (3) є:

Q ((x,y) R_Δ)=F(x+Δx,y+Δy)–F(x+Δx,y)–F(x,y+Δy)+F(x,y) =

=

= = (4)

Таким чином,

(5)

при умові, що всі границі існують.

Функція f(x,y) називається щільністю розподілу системи випадкових величин X та Y.

Таким чином, щільність розподілу системи представляє собою границю відношень ймовірності попадання в малий прямокутник до площі цього прямокутника, коли обидва його розміри прямують до нуля. Вираз f(x,y)dxdy називається елементом ймовірності.

Елемент ймовірності є ймовірність попадання в елементарний прямокутник зі сторонами dx, dy, який доторкується точки (x,y) (див. мал. з R_Δ ).

Ця ймовірність дорівнює об’єму елементарного паралелепіпеда, обмеженого f(x,y) з основою dxdy. Звідси

(6)

Геометрично ймовірність попадання в область D зображується об’ємом циліндричного тіла, обмеженого зверху поверхнею розпорядку f(x,y), а знизу областю D.

Із останньої формули ймовірність попадання в прямокутник R:

(7)

З іншого боку:

(8)

Дійсно функція розподілу F(x,y) є ймовірність попадання в нескінченний квадрат, який можна розглядати як прямокутник обмежений абсцисами -∞ і x, ординатами -∞ і y.

Властивості щільності розподілу f(x,y):

1. f(x,y)≥0, так це є границя відношення двох невід’ємних величин.

2. (9),

так як цей інтеграл є ймовірність попадання у всю площину XOY.

Геометрично це означає, що повний об’єм тіла, обмеженого поверхнею розподілу і площиною ХОУ, дорівнює 1.

Приклад 1.

Система двох випадкових величин (Х,У) підпорядкована закону розподілу з щільністю

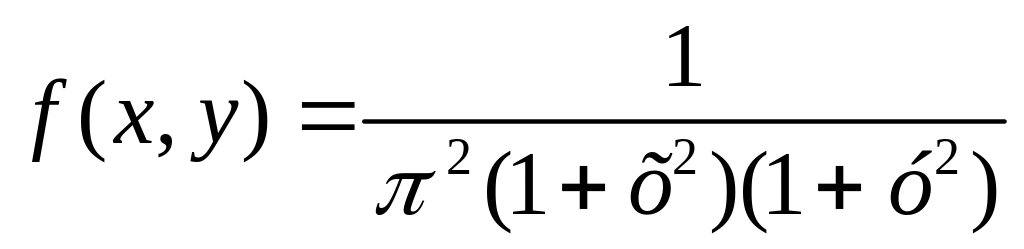
Знайти функцію розподілу F(x,y). Обчислити ймовірність попадання випадкової точки (х,у) в квадрат R

Приклад 2.

Поверхня розподілу системи (х,у) є прямий круговий конус з основою – круг радіуса R з центром в (0,0).

З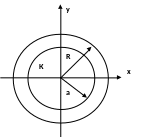 найти f(х,у) – ? Обчислити ймовірність того, що випадкова точка (х,у) попаде в круг К радіуса а, де а .

h

, де h – висота конуса

Висоту h визначаємо так, щоб об’єкт конуса був рівний 1:

Полярна система координат

Матриця Якобі І=