
- •Тема 5 символический (комплексный) метод расЧёТа цепей переменного синусоидального тока
- •5.1. Символическое изображение синусоидальных функций
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.2. Сложение и вычитание комплексных величин
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.3. Умножение и деление комплексных величин
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.4. Умножение вектора на j и на –j
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.5. Изображение производных и интегралов синусоидальных токов
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.6. Закон Ома в комплексной форме
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.7. Комплексная проводимость
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.8. Комплексные напряжения
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.9. Комплексные токи
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.10. Комплексная мощность
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.11. Законы Кирхгофа в комплексной форме
- •Вопросы для самоконтроля
- •Задания для самоконтроля
- •5.12. Методы расчёта цепей переменного синусоидального тока в комплексной форме
- •Вопросы для самоконтроля
- •Алгоритм изучения темы «Символический (комплексный) метод расчёта цепей переменного синусоидального тока»
- •5.1. Символическое изображение синусоидальных функций
- •5.7. Комплексная проводимость
- •5.8. Комплексные напряжения
- •5.9. Комплексные токи
- •5.10. Комплексная мощность
- •5.11. Законы Кирхгофа в комплексной форме
- •5.12. Методы расчёта цепей переменного синусоидального тока в комплексной форме
Вопросы для самоконтроля
Составьте алгоритм умножения двух комплексных величин.
Составьте алгоритм деления двух комплексных величин.
Задания для самоконтроля
Заданы
два комплексных числа: ![]() =
100 ej67
и
=
100 ej67
и
![]() =
20 ej37.
=
20 ej37.
Найти произведение этих комплексов и их частное от деления.
5.4. Умножение вектора на j и на –j
Допустим, что необходимо умножить вектор
![]() = Аej
на вектор j
=
ej90.
В соответствии с п.5.3:
j
= Aej(+90)
.
= Аej
на вектор j
=
ej90.
В соответствии с п.5.3:
j
= Aej(+90)
.
Изобразим векторы и j на комплексной плоскости (рис.5.4).
Т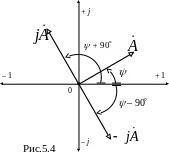 аким
образом, умножение
вектора на j
даёт вектор, равный по величине
предыдущему, но повернутый против
часовой стрелки относительно положения
предыдущего вектора на угол 90.
аким
образом, умножение
вектора на j
даёт вектор, равный по величине
предыдущему, но повернутый против
часовой стрелки относительно положения
предыдущего вектора на угол 90.
Умножим теперь этот же вектор на вектор –j = e– j90: (–j) = Aej(– 90) .
Итак, умножение вектора на –j даёт вектор, равный по величине предыдущему, но повернутый по часовой стрелке относительно положения предыдущего вектора на угол 90.
Вопросы для самоконтроля
Что даёт умножение любого вектора на комплексной плоскости на j ?
Что даёт умножение любого вектора на комплексной плоскости на –j ?
Задания для самоконтроля
Задано комплексное число: = 200 e–j30.
Найти комплексы
 и
и
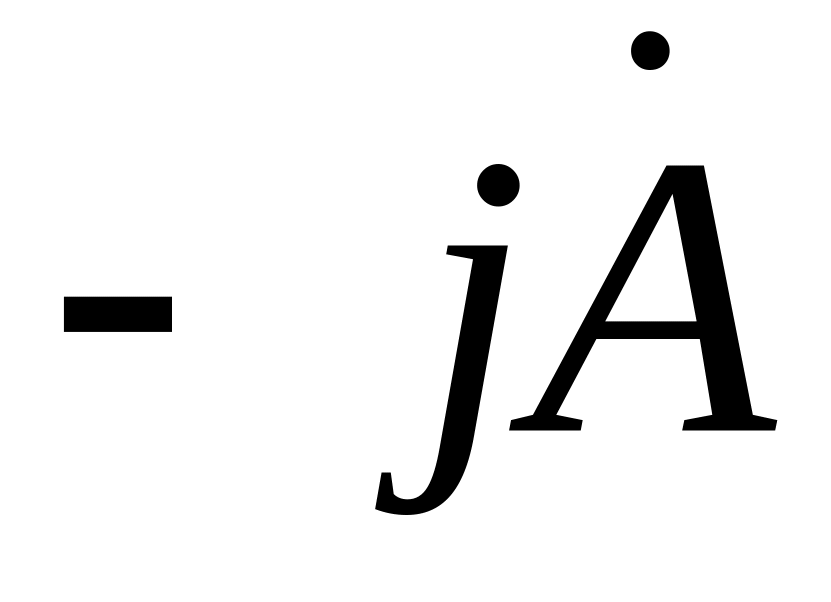 и изобразить их векторами на комплексной
плоскости.
и изобразить их векторами на комплексной
плоскости.
5.5. Изображение производных и интегралов синусоидальных токов
Пусть мгновенное значение тока i = Im sin(t + i) .
Комплекс этого тока
, т.е. і İm. |
(5.7) |
Возьмём производную тока:
|
|
Изобразим производную тока комплексом:
|
(5.8) |
т.е. |
|
Возьмём интеграл тока:
|
|
Изобразим интеграл тока комплексом:
|
(5.9) |
т.е. |
|
Таким образом, производная тока изображается комплексом тока, умноженным на j, а интеграл тока – комплексом тока, делённым на j.
Вопросы для самоконтроля
Как изобразить производную тока комплексом?
Как изобразить интеграл тока комплексом?
Задания для самоконтроля
Задано выражение мгновенного тока: i = 28,2 sin(t + 90) А.
Записать комплексы производной тока и интеграла тока –
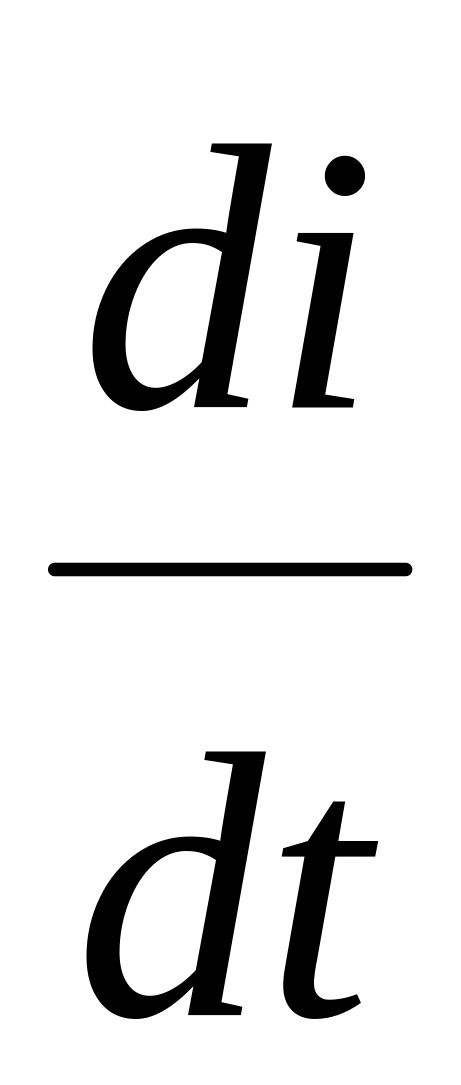 и idt.
и idt.
5.6. Закон Ома в комплексной форме
Рассмотрим расчётную схему цепи с последовательно соединёнными активным сопротивлением, индуктивностью и ёмкостью (рис.3.31).
Допустим, что в цепи протекает ток i = Im sin(t + i), напряжение источника u = Um sin(t + u).
В соответствии с первым законом Кирхгофа: u = ur + ul + uс ,
или |
(5.10) |
Перейдём теперь от оригиналов к изображениям:
|
ri rİm; |
|
|---|---|---|
|
|
|
|
|
|
Перепишем уравнение (5.10) с помощью изображений в комплексной форме:
|
(5.11) |
откуда изображение тока:
|
(5.12) |
Множитель
![]() представляет собой комплекс
полного сопротивления цепи, имеет
единицу измерения Ом и обозначается
Z
:
представляет собой комплекс
полного сопротивления цепи, имеет
единицу измерения Ом и обозначается
Z
:
|
(5.13) |
где r – активное сопротивление цепи, Ом;
х = хL – хс – реактивное сопротивление цепи, Ом.
Запишем закон Ома в комплексной форме для максимальных значений напряжения и тока:
|
(5.14) |
Из уравнения (5.14) находим:
|
|
где ![]() – модуль комплекса полного сопротивления
цепи, Ом.
– модуль комплекса полного сопротивления
цепи, Ом.
Комплекс полного сопротивления цепи и его составляющие изображаются на комплексной плоскости в виде треугольника (рис.5.5).

Модуль полного сопротивления:
|
|
Угол сдвига фаз:
|
|
или |
|


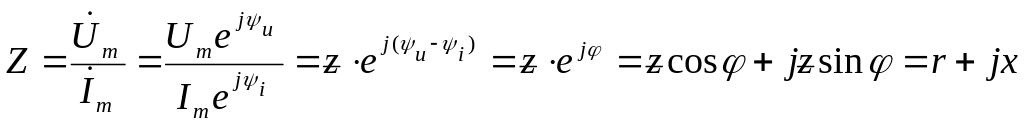 ,
,