Тема 5 символический (комплексный) метод расЧёТа цепей переменного синусоидального тока

5.1. Символическое изображение синусоидальных функций

До этого синусоидальные величины изображались векторами, начальная фаза которых отсчитывалась на плоскости от оси абсцисс со знаком «+». На плоскости вектор синусоидальной величины может проектироваться на ось ординат и ось абс­цисс. При этом сложение и вычитание векторов заменяется сложением и вычита­нием их проекций и по суммарным значениям проекций находится суммарный вектор. Но такие операции производить на обычной плоскости сложно, поэтому в электротехнике векторы синусоидальных величин изображают на комплексной плоскости.

Из курса математики известна формула Эйлера:

ej = cos  + jsin ,

(5.1)

где .

Комплексное число e^j изображают на комплексной плоскости вектором, ко­торый равен единице и образует угол  с осью действительных значений (осью +1), который отсчитывается против часовой стрелки от этой оси (рис.5.1).

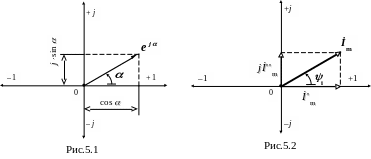
Модуль функции e^j равен единице:

.

Если вместо функции e^j взять функцию I_me^j, то на комплексной плоскости она, как и функция e^j, изображается вектором под углом  к оси +1, однако мо­дуль вектора в I_m раз больше (рис.5.2). Для синусоидального тока угол  = t + _i , векторы изображают для момента времени t = 0, поэтому вектор тока на комплексной плоскости записывается так:

.

(5.2)

Таким образом, оригинал тока i = I_m sin(t + _i) соответствует изображению (или символу), т.е. i  İ_m. Равенство (5.2) называют показательной формой за­писи комплексного тока İ_m.

Комплексный ток может быть записан в алгебраической форме:

,

(5.3)

где I'_m и I''_m – проекции тока соответственно на действительную

и мнимую оси (рис.5.2).

Комплексный ток может быть также записан в тригонометрической форме:

.

(5.4)

Величины I'_m = I_m cos_i и I''_m = I_m sin_i называют соответственно действи­тельной и мнимой частями комплексного тока İ_m.

При расчётах пользуются комплексным действующим значением тока, кото­рый в раз меньше комплексных амплитудных значений тока, т.е.:

,	(5.5)
где где .

Аналогично изображают комплексные э.д.с. и напряжения:

; ,	(5.6)
; .

Вопросы для самоконтроля

1. Запишите формулу Эйлера.

2. Что понимается под мнимым числом j ?

3. Как изображается комплексное число e^j на комплексной плоскости?

4. Чему равен модуль функции e^j ?

5. Как записать комплекс тока в показательной форме?

6. Как изобразить комплекс тока на комплексной плоскости?

7. Как записать комплекс тока в тригонометрической форме?

8. Как записать комплекс тока в алгебраической форме?

9. Как записать комплекс действующего значения тока в показательной форме?

10. Как записать комплекс действующего значения э.д.с. в показательной форме?

11. Как записать комплекс действующего значения напряжения в показательной форме?