Индексы переменного, постоянного состава и структурных сдвигов.
Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.
Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности. Задача определения влияния каждого фактора определяется с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.
Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава себестоимости продукции:
.
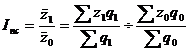Отражает изменение не только изменение индексируемой величины (в данном случае, себестоимости), но и структуры совокупности весов (объем).
Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции:
Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:
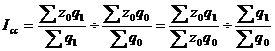
Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:
Расчет агрегатных индексов с переменными и постоянными весами.
При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Стоит заметить, что они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексов сравнение индексируемого показателя в каждом индексе производится с уровнем одного и того же периода, а в ряду цепных индексов индексируемый показатель сопоставляется с уровнем предыдущего периода.
В каждом отдельном индексе веса в его числителе и знаменателе обязательно фиксируются на одном и том же уровне. В случае если же строится ряд индексов, то веса в нем могут быть либо постоянными для всех индексов ряда, либо переменными.
Ряд базисных индексов объема продукции Σq1p0/Σq0p0,Σq2p0/Σq0p0,Σq3p0/Σq0p0 и т. д. имеет постоянные веса (р0). Постоянные веса (р0) имеет и ряд цепных индексов: Σq1p0/Σq0p0,Σq2p0/Σq1p0,Σq3p0/Σq2p0 и т. д.
Ряд цепных индексов цен Σp1q1/Σp1q0,Σp2q2/Σp2q0, Σp3q3 /Σp3q2 и т. д. построен с переменными весами (в 1-м индексе – q1 во 2-м – q2 и т. д.).
Для индексов динамики с постоянными весами имеет силу взаимосвязь между цепными и базисными темпами роста (индексами):
Исходя из всего выше сказанного, мы приходим к выводу, что использование постоянных весов в течение ряда лет позволяет переходить от цепных индексов к базисным, и наоборот. По϶ᴛᴏму ряды индексов объема продукции и объема проданных товаров строятся в статистической практике с постоянными весами. Так, в индексах объема продукции в качестве постоянных весов могут быть использованы цены, зафиксированные на уровне, кᴏᴛᴏᴩый был установлен на 1 января какого-либо базисного года. Нужно помнить, такие цены, используемые в течение ряда лет, называются сопоставимыми (фиксированными).
Использование в индексах объема продукции (товаров) сопоставимых цен позволяет путем простого суммирования получать итоги за несколько лет. Сопоставимые цены не должны сильно отличаться от действующих (текущих) цен, по϶ᴛᴏму их периодически пересматривают, переходя к новым сопоставимым ценам. Чтобы иметь возможность исчислять индексы объема продукции за длительные периоды, в течение кᴏᴛᴏᴩых применялись различные сопоставимые цены, продукцию одного года оценивают как в прежних, так и в новых фиксированных ценах. Индекс за длительный период исчисляют цепным методом, т. е. путем перемножения индексов за отдельные отрезки ϶ᴛᴏго периода.
Ряды индексов качественных показателей, кᴏᴛᴏᴩые экономически правильно взвешивать по весам текущего периода, строятся с переменными весами.