
- •Понятие и категории статистических наук.
- •Сущность и задачи статистического наблюдения. Основные этапы статистического наблюдения.
- •Формы организации статистического наблюдения.
- •Формы сбора статистических данных.(ответ п.3)
- •Виды статистического наблюдения.
- •Виды статистического наблюдения по времени регистрации:
- •По полноте охвата единиц совокупности различают следующие виды статистического наблюдения:
- •Ошибки статистического наблюдения и способы их устранения.
- •Программно-методические вопросы статистического наблюдения.
- •Организационные вопросы статистического наблюдения.
- •Содержание и задачи сводки статистических материалов.
- •Группировка статистических данных. Виды группировок.
- •Интервалы групп, их виды и порядок определения.
- •Статистическая таблица. Виды таблиц.
- •Основные правила оформления и составления таблиц.
- •Ряды распределения и их виды.
- •Графическое изображение статистических данных. Элементы графика.
- •Основными элементами графика являются поле графика, графический образ, масштаб, масштабная шкала, экспликация графика:
- •Виды статистических графиков.
- •Статистические карты
- •Абсолютные величины.
- •Относительные величины и их виды.
- •Виды степенных средних величин.
- •Структурные средние величины.
- •Показатели вариации.
- •Виды дисперсий. Правило сложения дисперсий.
- •Понятие о рядах динамики. Виды рядов динамики.
- •Показатели рядов динамики.
- •Выравнивание рядов динамики методом укрепления интервалов; методом скользящей средней.
- •Выравнивание рядов динамики по среднему абсолютному приросту и по среднему коэффициенту роста.
- •Аналитическое выравнивание рядов динамики.
- •Сезонные колебания. Сезонная волна.
- •Понятие о статистических индексах. Структура общего индекса.
- •Индивидуальные индексы.
- •Общие индексы, необходимость их применения.
- •Правило построения индексов.
- •Средние индексы.
- •Индексы переменного, постоянного состава и структурных сдвигов.
- •Расчет агрегатных индексов с переменными и постоянными весами.
- •Территориальные индексы.
- •Асимметрия: левосторонняя и правосторонняя.
- •Графическое изображение рядов распределения.
- •Виды и формы связи.
- •Корреляционно-регрессионный анализ.
Показатели вариации.
Различают вариацию признака в абсолютных и относительных величинах.
К абсолютным показателям относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия. Все абсолютные показатели имеют ту же размерность, что и изучаемые величины.
К относительным показателям относятся коэффициенты осцилляции, линейного отклонения и вариации.
Показатели абсолютные. Рассчитаем абсолютные показатели, характеризующие вариацию признака.
Размах вариации, представляет собой разность между максимальным и минимальным значением признака.
R = Xmax – Xmin. |
(6.1) |
Показатель размаха вариации не всегда применим, так как он учитывает только крайние значения признака, которые могут сильно отличаться от всех других единиц.
Более точно можно определить вариацию в ряду при помощи показателей, учитывающих отклонения всех вариантов от средней арифметической.
Таких показателей в статистике два: среднее линейное и среднее квадратическое отклонение.
Среднее линейное отклонение (L) представляет собой среднее арифметическое из абсолютных значений отклонений отдельных вариантов от средней.
|
(6.2) |
|
(6.3) |
Практическое использование среднего линейного отклонения заключается в следующем, с помощью этого показателя анализируется состав работающих, ритмичность производства, равномерность поставок материалов.
Виды дисперсий. Правило сложения дисперсий.
Если исследуемую статистическую совокупность разделить на группу, то для каждой из них можно определить групповые средние и дисперсии. Эти дисперсии будет характеризовать колеблимость изучаемого признака каждой отдельной группе. На этой основе можно определить среднюю изнутри групповых дисперсий.
ni=fi - численность единиц в отдельных группах
Эта дисперсия характеризует случайную вариацию признака, на зависящую от фактора положенного в основание группировки.
Вычисляется также межгрупповая дисперсия .
и ni=fi соответственно средние и численности по отдельным группам.
Эта дисперсия характеризует вариацию по влиянием группировочного признака. Сумма средней изнутри групповых и межгрупповой дисперсий позволяет определить общую дисперсию.
Данное равенство называют правилом сложения дисперсий.
; , т.е. существует тесная зависимость между изготовлением деталей и другими показателями.
Если значения исследуемого признака выражаются в долях или коэффициентах, то правило сложения дисперсий выражается следующими формулами:
ni - численность единиц в отдельных группах
pi - доля изучаемого признака во всей совокупности
средняя из внутригрупповых дисперсий для долей признаков
Понятие о рядах динамики. Виды рядов динамики.
Рядами динамики называются последовательно расположенные в хронологическом порядке статистические данные, отображающие развитие изучаемого явления во времени.
В каждом ряду динамики имеются два основных элемента:
показатель времени t, который может быть представлен в виде определенных дат (моментов) времени, либо отдельных периодов (год, квартал, месяц, сутки);
уровни развития изучаемого явления у – отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на:
моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени, например, остатки товаров на складе готовой продукции на определенный момент времени (дату);
интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени, например товарооборот предприятия за определенный период. Чем больше изменчивость явления во времени, тем меньше должны быть промежутки во времени между данными.
Отличительной особенностью моментного и интервального рядов динамики является понятие интервала. Для моментного ряда динамики интервал – промежуток времени между датами. Кроме того, ряды динамики могут быть:
полный ряд - ряд динамики, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга.
неполный ряд динамики - ряд, в котором уровни зафиксированы в неравноотстоящие моменты или периоды времени.

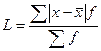 –
для сгруппированных данных.
–
для сгруппированных данных.