Побудова гіперболи за заданою вершиною a та фокусу f.

В основу цього способу покладено спосіб тріади.

Через точку A проводять пряму q₁ перпендикулярно осі AF гіперболи і коло q₂, радіус якого R = |AF|. Центр перетворення O₁ вибирають у фокусі, а O₂ – на відстані R/2 від точки A. Центр O_3¥ віддалений у нескінченність в напрямну осі гіперболи (рис.5.5).

Рисунок 5.5

Для побудови точок кривої q₃ проводять довільну пряму лінію паралельну O₁O₂ і відмічають точки 1 і 2 перетину прямої відповідно із прямою q₁ та колом q₂. Проводять прямі O₂1 та O₁2. Точка 3 перетину цих прямих належить кривій q₃.

Завдання № 2. "Комплексне креслення точки, прямої, площини". Виконується на аркуші формату A3.

При компонуванні креслення слід звернути увагу на розміщення осей та розміри таблиці (див. зразок на рис.3.2).

Послідовність виконання завдання:

1. Побудувати три проекції основи піраміди за заданими координатами точок 1, 2, 3 та з'єднати їх однойменні проекції.

2. За заданими координатами точки S побудувати три проекції вершини та з'єднати їх ребрами S1, S2, S3 з проекціями вершин основи піраміди.

3. Проаналізувати розташування прямих (ребер та сторін основи піраміди) у просторі. Для прямих загального положення визначити натуральну довжину методом прямокутного трикутника; щодо прямих особливого положення, то їхню натуральну довжину треба визначити та указати на відповідній площині проекцій. Результати занести у таблицю.

4. Визначити положення площин (граней та основ піраміди) у просторі шляхом аналізу розташування їхніх проекцій та заповнити таблицю.

5. Побудувати бокову розгортку піраміди методом трикутника, уявно розрізавши її по одному з ребер; потім до будь-якого боку основи прибудувати площину трикутника основи 123.

6. Точка  – контрольне запитання викладача при прийомі роботи.

Завдання № 3. "Перетин площин та визначення дійсної величини площини ΔABC". Виконується на аркуші формату A3.

Зразок завдання наведено на рис.3.3.

Задано координати шести точок A, B, C, D, E, F. Необхідно:

• побудувати двохпроекційне ортогональне креслення двох площин Q(ABC) і S(DEF);

• побудувати лінію MN взаємного перетину площин Q і S;

• установити видимість сторін і полів трикутників ABC і DEF у проекціях;

• визначити дійсну величину площини ΔABC методом обертання навколо головної лінії площини (горизонталі або фронталі).

Послідовність виконанню завдання:

Побудувати горизонтальну і фронтальну проекції трикутників ABC і DEF.

Побудову лінії взаємного перетину заданих площин Q і S рекомендується виконувати знаходженням точки M перетину відрізка BC з площиною S(DEF) і точки N перетину відрізка DE з площиною Q(ABC).

Алгоритм побудови лінії MN перетину площин Q і S:

1. Для побудови точки M виконують такі графічні операції:

а/ через відрізок BC проводять посередник – фронтально-проектуючу площину T.

б/ будують проекції лінії 12 перетину площин T і S.

2. Аналогічні графічні операції виконують для побудови точки N:

а/ через відрізок DE проводять посередник – горизонтально-проектуючу площину R;

б/ будують проекції лінії 34 перетину площин S і R.

3. З'єднують однойменні проекції загальних точок для площин, що перетинаються.

4. Установлюють видимість сторін і полів трикутників ABC і DEF у проекціях. Для цього використовують фронтально-конкуруючі точки 2 і 5. та горизонтально-конкуруючі точки 3 і 6 (точки M і N – межі видимості).

Алгоритм визначення дійсної величини площини ΔABC.

1. Будують двохпроекційне ортогональне креслення площин Q(ABC);

2. Будують горизонталь h(h₁, h₂) ΔABC, яка проходить через точку A.

3. Через точку B проводять горизонтально-проектуючу площину Q перпендикулярно до горизонталі h.

4. Знаходять точку O(O₁, O₂) перетину площини Q з горизонталлю h – центр обертання точки B

5. Знаходять проекції радіуса обертання точки B навколо горизонталі (B₁O₁, B₂O₂) та його дійсну величину методом прямокутного трикутника O₁B₀.

6. Повертають площину ΔABC навколо горизонталі h так, щоб вона стала площиною горизонтального рівня. Для цього на горизонтальному сліді площини Q(h₁⁰) відкладають дійсну величину радіуса обертання O₁B₀ і отримують повернуту точку .

7. Повернуту точку отримують як точку перетину прямої 1₁ з горизонтально-проектуючою площиною, проведеною через точку C перпендикулярно до горизонталі h.

8. З'єднують точи і з точкою A₁. Отриманий ΔA є дійсною величиною ΔABC.

Завдання № 4. Визначення відстані від точки до площини та побудова площини, паралельної заданої. Виконується на форматі A3.

Зразок завдання наведено на рис.3.4.

Задано координати чотирьох точок A, B, C, D. Необхідно:

Визначити відстань l від точки D до площини P(ΔABC);

Побудувати площину Q паралельну площині P і віддалену від неї на відстань l₁ = 1,5l;

Визначити дійсну величину ΔABC методом заміни площин проекцій.

Послідовність виконання завдання:

1). Побудувати горизонтальну і фронтальну проекції ΔABC;

2). Провести в площині ΔABC головні лінії – горизонталь h і фронталь f;

3). Провести проекції перпендикуляра n із точки D до площини ΔABC ( ; );

4). Визначити точку K зустрічі перпендикуляра n із площиною ΔABC (див. завдання 3). Методом прямокутного трикутника визначаємо дійсну величину l = DK (відстань від точки D до площини P(ΔABC).

5). На дійсній величині DK від точки K відкладаємо відрізок KT = l₁ = 1,5l і визначаємо проекції точок T(T₁, T₂).

6). Через точку T проводимо площину Q, задавши її двома прямими a і b що перетинаються, і які відповідно паралельні прямим AB і AC площини P(ΔABC) – (a || AB, b || AC).

7). Методом заміни площин проекцій перетворимо площину ΔABC у проектуючу, для чого введемо нову систему площин проекцій П₁П₄, замінивши площину П₂ на П₄. Площину П₄ вибираємо перпендикулярно до площини П₁ і перпендикулярно до горизонталі площини ΔABC ( ). У системі площин П₁П₄ площина ΔABC стала проектуючою (A₄B₄C₄). Вводимо нову систему площин проекцій П₅П₄, замінивши площину П₁ на П₅. Площину П₅ вибираємо перпендикулярно до площини П₄ і паралельно площині ΔABC. Площина ΔABC стала площиною рівня і на площину проекцій П₅ спроектується в дійсну величину.

Завдання № 5. Визначення дійної величини двогранного кута при ребрі піраміди. Виконується на форматі A3.

Побудувати проекції піраміди, основою якої є трикутник ABC, а ребро SA визначає висоту h піраміди. Визначити дійсну величину двогранного кута φ при ребрі BC.

Приклад виконання завдання наведено на рис.3.5.

Послідовність виконанню завдання:

За координатами будують горизонтальну та фронтальну проекції трикутника основи піраміди ABC.

Проводять горизонталь С1(С₁1₁, C₂1₂) і фронталь 12(1₁2_І, 1₂2₂) у площині трикутника. Знаючи, що горизонтальна проекція перпендикуляра перпендикулярна горизонтальній проекції горизонталі, а фронтальна – фронтальній проекції фронталі площини ΔABC, в точці A будують перпендикуляр AD(A₁D₁, A₂D₂) до площини трикутника.

Оскільки перпендикуляр є прямою загального положення, то визначають дійсну довжину A₂D₀ довільного відрізка висоти піраміди. На відрізку A₂D₀ дійсних довжин відкладають задану висоту h(A₂S₀) піраміди і знаходять вершину піраміди S(S₁, S₂). На рис.3.5. визначення проекцій S₁ і S₂ вершини S піраміди показано двома способами – способом прямокутного трикутника і способом плоскопаралельного переміщення. Задачу виконати одним із наведених способів.

Будують ребра піраміди. За допомогою конкуруючих точок встановлюють їх видимість.

При визначенні дійсної величини двогранного кута при ребрі ВС треба пам'ятати, що двогранний кут зобразиться на площину проекцій у дійсну величину в тому випадку, коли ребро ВС спроектується у точку, тобто стане проектуючим відносно площини проекцій. Такого результату можна досягти шляхом заміни двох площин проекцій.

Отже, проводять вісь Х₁₄ нової системи площин проекцій паралельно В₁С₁ (з метою розміщення побудов на епюрі вісь Х₁₄ зміщено дещо вправо та вниз) і будують нові фронтальні проекції A₄, B₄, C₄, S₄ вершин двогранного кута (для побудови координати вершин беруть з фронтальної площини проекцій і відкладають їх на лініях зв'язку від осі Х₁₄). У новій системі координатних площин проекцій П₁П₄ ребро ВС стало фронтальним рівня.

Другу нову вісь проекцій Х₄₅ проводять перпендикулярно B₄C₄ (з метою розміщення побудов на епюрі вісь Х₄₅ зміщено дещо вправо і вниз)і будують нові горизонтальні проекції A₅, B₅, C₅, S₅ вершин двогранного кута ABSC. При цьому ребро ВС на П₅ спроектується у точку, а грані – у лінії, які обмежують шуканий кут φ.

Завдання № 6. “Переріз 2-х поверхонь проектуючою площиною”. Виконується на аркуші формату A3 (або на двох форматах А4).

Зразок виконання наведено на рис.3.6.

Задано дві проекції геометричних тіл, зрізаних проектуючою площиною, і одна проекція точки M, яка належить поверхні. Необхідно побудувати:

• третю (профільну) проекцію геометричного тіла;

• проекції фігури перерізу;

• натуральну величину (площу) фігури перерізу;

• відсутні проекції точки М;

Послідовність виконанню завдання.

Для усіх варіантів основи геометричних фігур вписані в коло, діаметр якого дорівнює 60 мм, висота фігур становить 80 мм. На відповідній площині проекцій (П₁ або П₂) проводять коло радіусом 30 мм. У коло вписують фігуру основи (многокутник для призми і піраміди). Для тіл обертання це коло є горизонтальною (фронтальною) проекцією геометричного тіла. Після цього будують фронтальну (горизонтальну) і профільну проекції і намічають сліди проектуючої січної площини Σ.

Приступаючи до побудови лінії перерізу, студент повинен знати властивість проектуючої площини. Ця властивість полягає у тому, що з її слідом-проекцією збігаються проекції усіх точок, ліній і плоских фігур, які належать їй. Отже, одна проекція фігури перерізу збігається зі слідом-проекцією площини Σ. Будують другу і третю проекції перерізу.

Для визначення натуральної величини фігури перерізу пропонується використати метод заміни площин проекцій. У результаті заміни площин проекцій плоска фігура і її елементи зобразяться без спотворення.

Побудова відсутніх проекцій точки M, що належить основі фігури, не потребує додаткових пояснень. Якщо точка M знаходиться на бічній поверхні фігури, то для побудови відсутніх проекцій користуються допоміжними січними площинами або твірними.

Завдання № 7. Побудова точок зустрічі прямої з поверхнею геометричного тіла. Виконується на форматі A4.

Зразок виконання наведено на рис.3.7а, 3.7б.

Необхідно:

1). Через пряму провести допоміжну площину.

2). Побудувати лінію перерізу поверхні допоміжною площиною.

Примітка. Для спрощення рішення задачі слід вибирати допоміжну площину таким чином, щоб проекція перерізу була найпростішою.

3). На перетині побудованої лінії перерізу та прямої позначити проекції точок перетину з заданою поверхнею.

На рис.3.7а показано як знайдено точки перетину прямої a з трьохгранною пірамідою, а на рис.3.7б – прямої AB з нахиленим конусом.

Через пряму a (рис.3.7а) проведена допоміжна фронтально - проектуюча площина P(P≡f⁰₂). Ця площина перетинає кожне з ребер AS, BC і CS в точках 1, 2, 3, відповідно. Утворений переріз у вигляді трикутника Δ123 перетинається з заданою прямою a в точках 4 та 5.

Через пряму AB і вершину конуса S (рис.3.7б) проведена допоміжна площина загального положення. Ця площина перетинає конус по твірним S2 і S3. Утворений переріз перетинається з заданою прямою AB в точках K та L.

Завдання № 8. Побудова проекцій геометричного тіла з отвором та виконати перетин його проектуючою площиною. Виконується на форматі A3.

Приклад виконання завдання наведено на рис.3.8.

Необхідно:

Побудувати три проекції геометричного тіла з наскрізним отвором, проекції перетину його проектуючою площиною Q і натуральну величину площини перетину.

Послідовність виконання завдання:

• Побудувати три проекції геометричного тіла з отвором;

• Побудувати лінію взаємного перетину геометричного тіла з поверхнею отвору, використовуючи належність точок лінії взаємного перетину, поверхні геометричного тіла.

• Побудувати проекції та натуральні розміри площини перетину методом заміни площини проекцій, використовуючи досвід попередніх креслень (див. завдання 6).

• На кресленні розміри не ставити, обвід зображення виконати з урахуванням видимості.

Завдання № 9. Побудова проекцій геометричного тіла з двома отворами та виконати перетин його проектуючою площиною. Виконується на форматі A3.

Приклад виконання завдання наведено на рис.3.9.

Необхідно:

Побудувати третє зображення деталі за двома даними, виконати розрізи і натуральний вигляд похилого перерізу.

Зображення багатьох деталей машинобудування ускладнюється наявністю в їхніх формах різних отворів, зрізів, вирізів. Особливу складність у зображенні деталей машин становить наявність трьох поверхонь, які взаємно перерізуються (подвійне проникання). Практично мають місце найрізноманітніші варіанти складних геометричних тіл у формах деталей, які потребують найбільш раціональних способів їх зображення.

Такі деталі мають співвісні наскрізні отвори і фронтально проектуючі наскрізні циліндричні або призматичні отвори.

Геометричне тіло (рис.5.6) являє собою призматичну поверхню 1, основа якої належить горизонтальній площині проекцій П₁, наскрізний циліндричний отвір 2. Вертикальну трикутну призму перерізує трикутний призматичний отвір 3, поверхня якого обмежена фронтально проектуючими площинами F(F₂), Ф(Ф₂) і горизонтальною площиною Σ(Σ₂).

По положенню у просторі отвір 2 – це горизонтально - проектуюча циліндрична поверхня, отвір 3 – фронтально - проектуюча поверхня. Отже, проекції лінії їхнього перетину на відповідних проекціях збігаються із зображенням цих поверхонь.

Зображення лінії перетину горизонтально - проектуючої призми з фронтально проектуючою призматичною поверхнею на профільній площині проекцій побудовано за допомогою точок 1, 2, 3 обрису отвору. Профільна проекція лінії перерізу фронтально - проектуючої призми з задньою гранню вертикальної призми збігається з її проекцією, оскільки вона е фронтальною гранню.

Побудова зображення лінії взаємного перерізу циліндра з трикутною призмою зрозуміла з рис.5.6 (побудова точок 4 і 5).

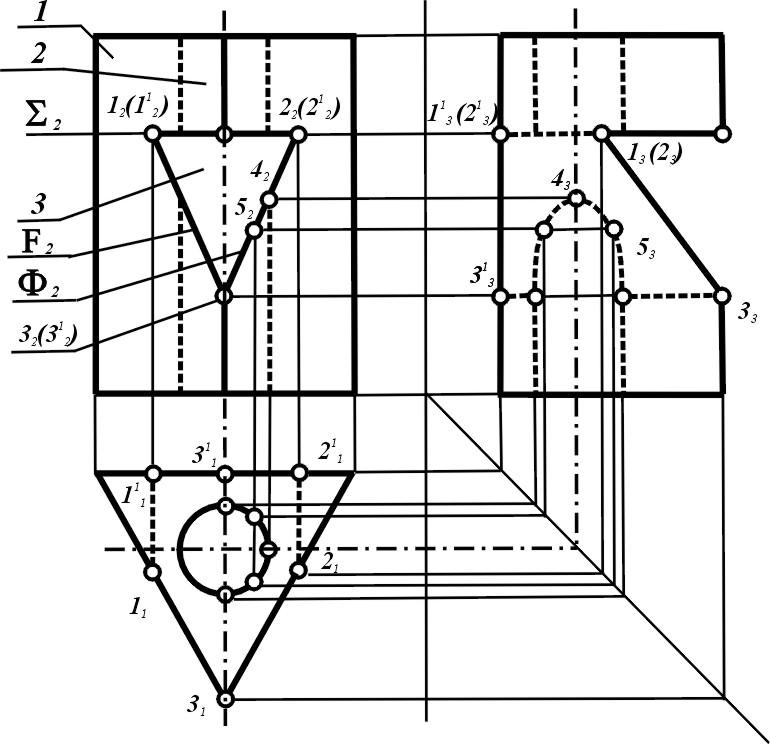
Рисунок 5.6

Зображення на кресленні в залежності від їхнього змісту діляться на види, розрізи і перерізи.

Розглянуті на рис.5.6 зображення виробу на трьох площинах проекцій в інженерній графіці мають інші, ніж у нарисній геометрії, назви: фронтальну проекцію називають видом спереду, або головним видом, горизонтальну – видом зверху, профільну – видом зліва.

Для зменшення кількості зображень допускається на виглядах показувати невидимі частини поверхні предмета за допомогою штрихових ліній.

Деталь, що розглядається, має отвори, які не повністю виявляються на видах. Невидний внутрішній обрис показаний штриховими лініями. Таке креслення незручне для читання. Щоб виявити внутрішню будову деталі, слід виконати відповідні розрізи та перерізи.

При виконанні розрізу або перерізу деталь розсікають уявною площиною і видаляють ту частину, яка знаходиться між спостерігачем і січною площиною. Плоску фігуру, одержану при цьому, називають перерізом. Переріз на кресленні виділяють штриховою. Якщо показати, крім перерізу, ще й видимі поверхні, які розташовані за січною площиною, то одержимо розріз.

Положення січної площини на кресленні позначають розімкнутою лінією, а напрям погляду показують стрілками. Розімкнута лінія не повинна перетинати основний контур відповідного зображення. Розміри розімкнутої лінії наведено на рис.5.7а, а розміри стрілки – на рис.5.7б. Із зовнішнього боку стрілок пишуть однакові великі літери українського алфавіту. Літерні позначення декількох розрізів присвоюють в алфавітному порядку без повторень і пропусків за виключенням літер Й, О, X, Ь, І, Ї. Розріз (переріз) позначають за типом А-А (завжди двома літерами, через тире).

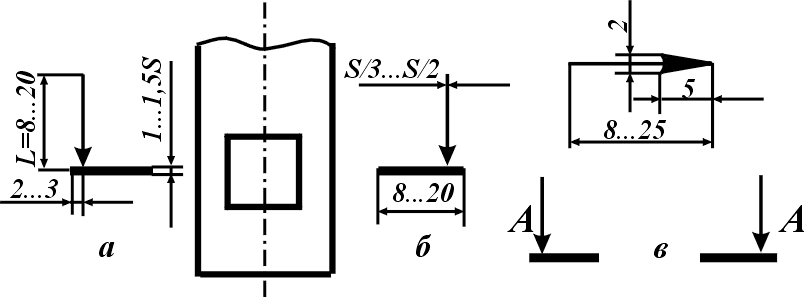
Рисунок 5.7

Прості розрізи позначають не завжди. Їх не позначають, якщо січна площина збігається з площиною симетрії деталі, а розріз розміщено безпосередньо на місці відповідного вигляду. На рис.5.8 і 5.9 фронтальні розрізи не позначено, оскільки січна площина збігається з площиною симетрії деталі.

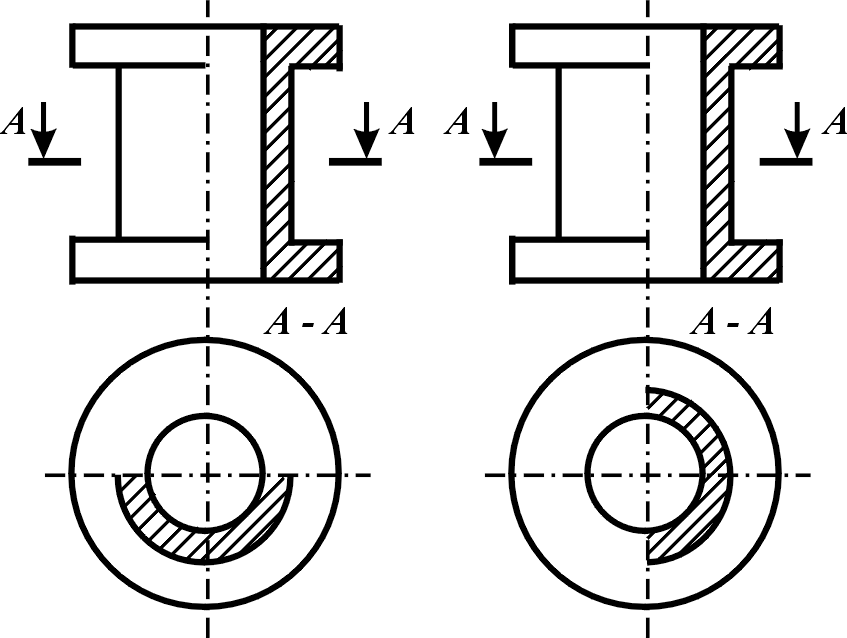
Рисунок 5.8 Рисунок 5.9

Якщо вид і розміщуваний на його місці розріз – фігури симетричні, то можна поєднати половину вигляду і половину розрізу. Лінією розділення їх є вісь симетрії (рис.5.8, 5.9). При цьому треба пам'ятати, що на головному виді зліва (справа) розріз звичайно розміщують праворуч від вертикальної осі симетрії (рис.5.8, 5.9), а на видах зверху (знизу) – нижче горизонтальної (рис.5.8) або праворуч (рис.5.9) від вертикальної осі симетрії.

Якщо контурна лінія предмета збігається з віссю симетрії, то вдаються до поєднання двох зображень: частини вигляду з частиною відповідного розрізу. Ці зображення розділяють суцільною хвилястою лінією так, щоб зберегти зображення контурної лінії (наприклад ребра) (рис.5.10).

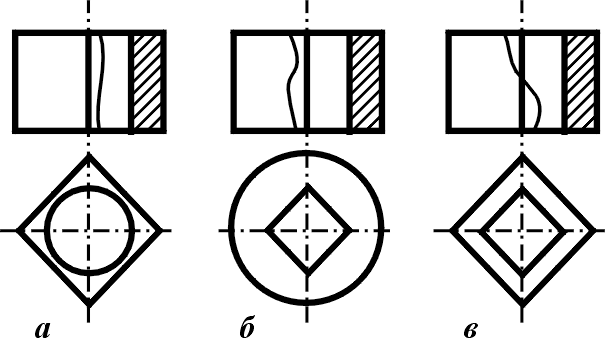
Рисунок 5.10

На зразку (рис.3.9) виконано горизонтальний А-А, фронтальний Б-Б і профільний розрізи. На кресленні горизонтальний і фронтальний розрізи, які виконано уявними площинами А і Б, позначено тому, що січні площини не збігаються з площинами симетрії деталі. Профільний розріз не позначено, оскільки січна площина збігається з площиною симетрії деталі.

При виконанні горизонтального і фронтального розрізів збережено ребра, які збігаються з осями симетрії деталі, – зовнішнє переднє ребро трикутної вертикальної призми і внутрішнє фронтально – проектуюче ребро трикутного отвору.

Деяким студентам на початку засвоєння проекційного креслення важко орієнтуватись у визначенні лінії перерізу і розташування відповідного розрізу. Тут потрібно пам'ятати: якщо розріз виконано горизонтальною січною площиною, то він може бути зображений лише на місці виду зверху, тому що тільки на цьому виді проектується у дійсну величину все, що розміщено у горизонтальній площині. Позначення лінії перерізу горизонтального розрізу може бути зроблено на головному виді або виді зліва.

Вертикальні розрізи можуть бути розміщені: фронтальний – на місці головного виду (слід січної площини позначається на виді зверху або зліва), профільний – на виді зліва (слід січної площини позначається на вигляді зверху або головному вигляді).

Опрацювавши розглянуті вище положення, приступають до виконання необхідних розрізів (рис.3.9): горизонтального (розріз А-А), фронтального (розріз Б-Б) і профільного. Після цього наносять виносні і розмірні лінії і, впевнившись у правильності всіх побудов, виконують штриховку розрізів (на всіх зображеннях штриховка виконується однаково для одного геометричного тіла) і обводять креслення лініями потрібної товщини.

Закінчивши виконання перших двох частин завдання, приступають до виконання похилого перерізу В-В. Уявну січну площину вибирають так, щоб вона проходила через вертикальний і фронтально проектуючій отвори (див. рис.3.9).

При побудові дійсної величини похилого перерізу слід мати на увазі, що переріз предмета будується як сукупність похилих перерізів геометричних тіл, з яких складається предмет.

На практиці похилі перерізи виконують без збереження проекційного зв'язку. Тому на вільному полі креслення проводять лінію a паралельно січній площині В і на ній відкладають фіксовані точки 1₂, 2₂, 3₂, які одержані у перетині сліду В-В січної площини В з відповідними фронтальними проекціями ребер даної деталі. Через точку 2₂ проводять перпендикулярно лінії a вісь симетрії фігури перерізу і на ній відкладають висоту y трикутника 123, яку беруть на вигляді зверху, і відмічають точку 3. 1₂23₂ – дійсна величина фігури перерізу вертикальної трикутної призми. З цієї фігури видаляють призматичний отвір шляхом накладання на неї перерізу трикутної фронтально - проектуючої призми. Для цього відкладають від осі симетрії 2₂2 відрізки, сума яких дорівнює ширині отвору (на рис.3.9 ці відрізки умовно позначені) і через одержані точки проводять лінії паралельно осі. Потім накладають фігуру перерізу циліндричного отвору. Побудова частини еліпса зрозуміла з рис.3.9. Одержану фігуру перерізу обводять лініями необхідної товщини, виконують штриховку і роблять напис “В-В”.

Завдання № 10. “Взаємний перетин поверхонь”. Виконується на форматі A3.

Задано дві проекції геометричних тіл, які взаємно перетинаються. Необхідно побудувати:

• третю проекцію геометричних тіл, що перетинаються;

• проекції лінії їх взаємного перетинання.

Приклад виконання завдання – на рис.3.10.

Послідовність виконання завдання:

До того, як розпочати побудову проекцій лінії перерізу заданих геометричних тіл, студент повинен за підручником детально познайомитися з методами побудови ліній перерізу поверхонь.

Існують три методи побудови ліній перерізу: метод допоміжних січних площин, метод допоміжних концентричних сферичних поверхонь та метод ексцентричних сферичних поверхонь.

Яким би методом не виконувалася побудова лінії перерізу, необхідно спочатку побудувати опорні точки цієї лінії. До них належать:

• точки, проекції яких лежать на проекціях обрисових ліній поверхонь;

• “крайні” точки – найвищі й найнижчі, праві й ліві – найближчі та найдальші від площин проекцій;

• точки, які відокремлюють видиму частину лінії від невидимої.

Визначивши на кресленні всі характерні точки, розпочинають побудову проміжних точок.

На рис.3.10 показано оформлення графічної роботи на прикладі взаємного перерізу прямого кругового конуса з фронтально - проектуючим циліндром. У даному разі фронтальна проекція лінії перерізу збігається з фронтальною проекцією циліндра. Задача зводиться до побудови горизонтальної і профільної проекцій лінії перерізу.

Виділяють на фронтальній і профільній проекціях опорні точки 1 (найнижча) і 5 (найвища). Профільні проекції 1₃ і 5₃ названих точок знаходяться у перетині обрисових твірних конуса і циліндра, а горизонтальні їх проекції 1₁ і 5₁ знайдені за допомогою перерізу конуса і циліндра горизонтальними площинами Δ і Δ¹. Горизонтальну проекцію опорної точки 3 – точки, яка відокремлює видиму частину лінії від невидимої відносно горизонтальної площини проекцій, знайдено за допомогою перерізу конуса і циліндра горизонтальною площиною Δ¹¹. Профільну проекцію знайдено у перетині горизонтальної і горизонтально-вертикальної ліній зв’язку.

Достатню кількість проміжних точок 2, 4, ... побудовано за допомогою допоміжних січних площин Σ, Σ¹, ....

Для засвоєння теми "Перетин поверхонь" студент повинен ознайомитися з такими методами: метод допоміжних січних площин та метод концентричних сфер.

З першим із вказаних методів студент вже знайомився при виконанні завдань 6 - 9.

Нижче розглянуто використання метода концентричних сфер при побудові лінії перетину конуса та похилого кругового циліндра (рис.5.11). Цей метод рекомендується використовувати для тіл обертання, осі яких перетинаються і утворюють площину рівня.

Для рішення задачі відзначимо опорні точки 1 і 3. Як видно з креслення (рис.5.11), фронтальні проекції зазначених точок знаходяться на перетинанні фронтальних нарисів заданих поверхонь, тому що осі поверхонь перетинаються, а їхня загальна площина симетрії паралельна площині П₂. Горизонтальні проекції 1₁ і 3₁ знаходимо по проекційних зв'язках.

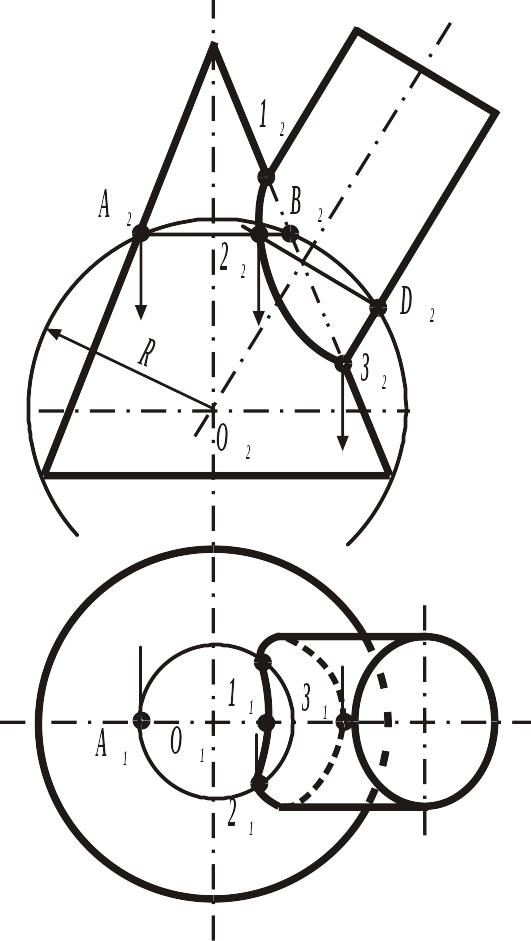
Рисунок 5.11

Для побудови довільних точок кривої перетинання доцільно скористатися посередниками – концентричними сферами з центром у точці O - перетинання осей поверхонь і радіусом сфери R, що лежить у наступних межах: Rmax відповідає відстані від центра до найбільш вилученої опорної точки (у розглянутої прикладі точка 1); Rmin у залежності від розташування центра сфер і іншої опорної точки (точка 3) може приймати два значення: або відповідає відстані від центра до найближчої опорної точки, або відповідає радіусу сфери, яка вписана в одну з поверхонь і перетинає іншу.

Зазначені сфери перетинають поверхні обертання по колах, що на фронтальну площину П₂ проектуються у відрізки прямих.

Розглянемо докладніше побудову двох точок 2 і 4.Сфера довільного радіуса R перетне конус по колу діаметра АВ, а циліндр по колу діаметра CD. На перетинанні проекцій кіл А₂В₂ і C₂D₂ одержимо проекції 2₂, 4₂ шуканих точок 2 і 4. Тому що вісь конуса перпендикулярна площини проекцій П₁, то коло діаметра АВ на площину П₁ проектується в коло. По проекційним зв'язкам знаходимо на горизонтальній проекції цього кола проекції 2₁ і 4₁ точок, що належать лінії перетинання.

Аналогічно відшукують проекції інших точок, що належать лінії перетинання, проводячи з центра O ряд сфер різного радіуса.

Завдання № 11. Побудова аксонометричних проекцій геометричних тіл. Виконується на двох форматах A4.

Приклад виконання завдання – на рис.3.11а, 3.11б.

Необхідно накреслити:

• геометричні тіла із завдань 6 та 9 в прямокутній диметрії та прямокутній ізометрії. При цьому слід врахувати, що гранні тіла слід виконувати в прямокутній симетрії.

Приступаючи до виконання аксонометричних проекцій предметів, студент повинен спочатку вивчити теоретичний матеріал за підручником, а також керуватись викладеним нижче.

Аксонометричні проекції застосовують для наочного зображення предметів або їх частин.

Необхідно пам’ятати, що слово “аксонометрія” означає вимірювання за осями або паралельно осям.

З п'яти стандартних аксонометричних проекцій, програмою передбачається вивчення прямокутної ізометрії та диметрії.

Якщо позначити коефіцієнти спотворення u за віссю O¹X¹, v – за віссю O¹Y¹, а w – за віссю O¹Z¹, то для прямокутної ізометрії теоретичні коефіцієнти спотворення рівні, тобто u = v = w = 0,82, для прямокутної диметрії u = w = 0,94, а v = 0,47.

При побудовах на практиці користуватися теоретичними коефіцієнтами спотворення не зовсім зручно, тому стандарт рекомендує практичні коефіцієнти спотворення: для прямокутної ізометрії u = v = w = 1, а для диметрії u = w = 1, v = 0,5. Побудоване таким чином зображення збільшується: в ізометрії в 1/0,82=1,22, а в диметрії в 1/0,94=1,06 рази, тобто масштаб зображення відповідно буде MA 1,22 : 1 і MA 1,06 :1.

Положення осей ізометричної проекції наведено на рис.5.12а. Осі O¹X¹ і O¹Y¹ розташовують під кутом 30º до горизонтальної лінії (120° між осями).

Рисунок 5.12а

На рис.5.12б показано положення осей для прямокутної диметрії.

Рисунок 5.12б.

Розглянемо побудову аксонометричної проекції на конкретному прикладі.

Нехай задано точку B(20, 25, 30) (рис.5.13а). Необхідно побудувати ізометричну проекцію цієї точки.

Для побудови аксонометричної проекції можна рекомендувати один із способів:

а) Координатний спосіб.

На осі O¹X¹ (рис.5.13б) відкладають відрізок x_B і з його кінця проводять пряму, яка паралельна осі O¹Y¹. На цій прямій відкладають координату y_B. Одержують точку B¹₁, вторинну проекцію точки B. З цієї точки проводять пряму, що паралельна осі O¹Z¹, на якій відкладають z_B. Точка B¹ – аксонометрична проекція точки B.

б) Метод вторинних проекцій.

На осі O¹X¹ (рис.5.13в) від точки O¹ відкладають відрізок x_B і з його кінця проводять прямі, які паралельні осям O¹Y¹ і O¹Z¹. На цих прямих відкладають відповідно координати y_B і z_B. Одержують B¹₁ і B¹₂ – вторинні горизонтальну і фронтальну проекції точки B. Із точки B¹₁ проводять пряму, яка паралельна осі O¹Z¹, а із точки B¹₂ – пряму, яка паралельна осі O¹Y¹. Точка B¹ перетину цих прямих – аксонометрична проекція точки B.

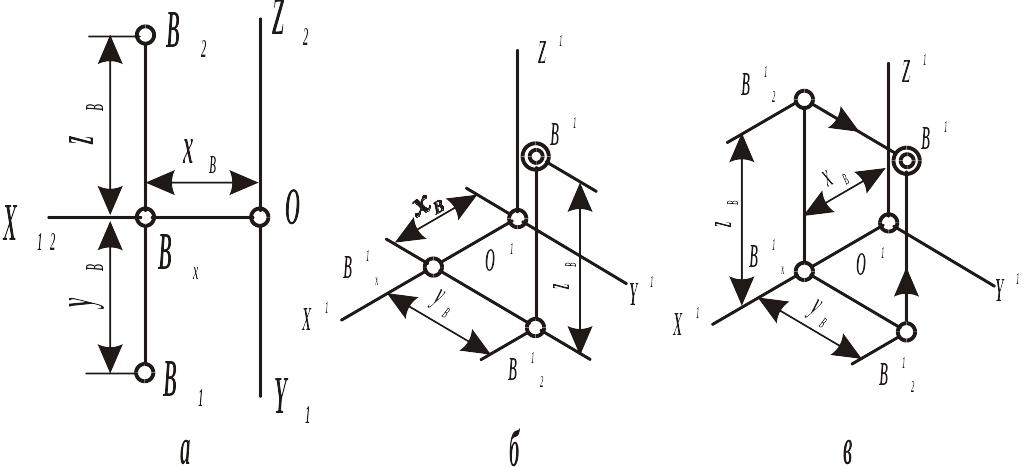
Рисунок 5.13

Прямокутна ізометрія кола

Кола, які розташовані у координатних або паралельних їм площинах, у прямокутній ізометрії зображуються еліпсами (велика вісь еліпса завжди перпендикулярна тій ізометричній осі, до якої перпендикулярна площина кола у просторі).

У прямокутній ізометрії однакові кола, які розташовані у координатних площинах, зображуються в однакові еліпси (рис.5.12а). Велика вісь еліпса при використанні практичних коефіцієнтів спотворення дорівнює 1,22d, мала – 0,71d (d- діаметр зображуваного кола).

Діаметри кіл, що паралельні координатним осям, зображуються відрізками, які паралельні, ізометричним осям, і дорівнюють діаметру кола. На рис.5.12а показано розташування осей еліпсів.

На практиці прийнято замінювати еліпси у прямокутній ізометрії овалами, що значно спрощує побудову. Осі овалів такі ж за довжиною, як і еліпсів.

Прямокутна диметрія кола.

У прямокутній диметрії однакові кола діаметром d, що розташовані у координатних площинах XOY і YOZ, проектуються в однакові еліпси, велика вісь яких дорівнює 1,06d, мала – 0,35d, за умови, що користуємося практичними коефіцієнтами спотворення. Коло, розташоване у площині XOZ, проектується в еліпс з осями: велика вісь дорівнює 1,06d, мала – 0,95d (рис.5.12б).

Діаметри кола, які паралельні координатним осям, проектуються у відрізки, що паралельні осям диметрії із спотвореннями, які відповідають осям.

На практиці еліпси замінюють чотирьох центровими овалами.

Для побудови аксонометрії кола, що розташоване у проектуючій площині чи площині загального положення, треба виділити на колі ряд точок, побудувати аксонометрію цих точок координатним способом і з’єднати їх плавною кривою. Це і буде шуканий еліпс – аксонометрія кола.

Як правило, аксонометричну проекцію деталі будують за ортогональним кресленням. Побудову слід виконувати відносно розташуванню осям проекцій деталі на ортогональному кресленні (побудова буде більш проста, якщо положення виробу відносно координатних осей O¹X¹, O¹Y¹ і O¹Z¹ залишається таким же, як і на ортогональному кресленні). Головний вигляд слід розміщувати на фронтальній площині проекцій.

Найчастіше на аксонометричних проекціях, коли виріб представляє собою симетричну фігуру, вирізають одну четверту або одну восьму частину деталі.

На аксонометричних проекціях, як правило, не застосовують повних розрізів, оскільки це зменшує зорову повноту зображення.

При виконанні розрізів вибирають уявні січні площини, які паралельні координатним площинам. Площини перерізів штрихують.

Лінії штрихування перерізів у аксонометричних проекціях наносять паралельно одній з діагоналей проекцій квадратів, що лежать у відповідних координатних площинах, сторони яких паралельні аксонометричним осям (рис.5.14 – для ізометрії та рис.5.15 – для диметрії).

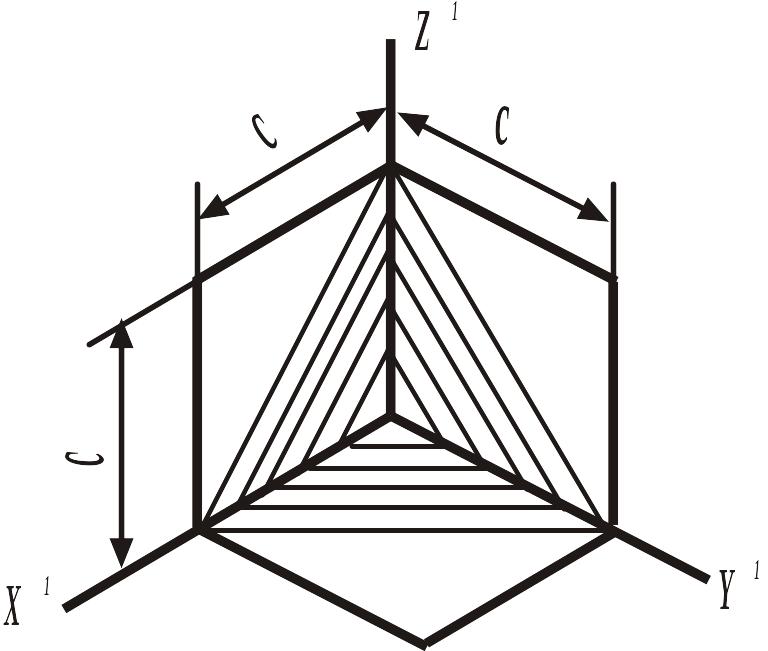
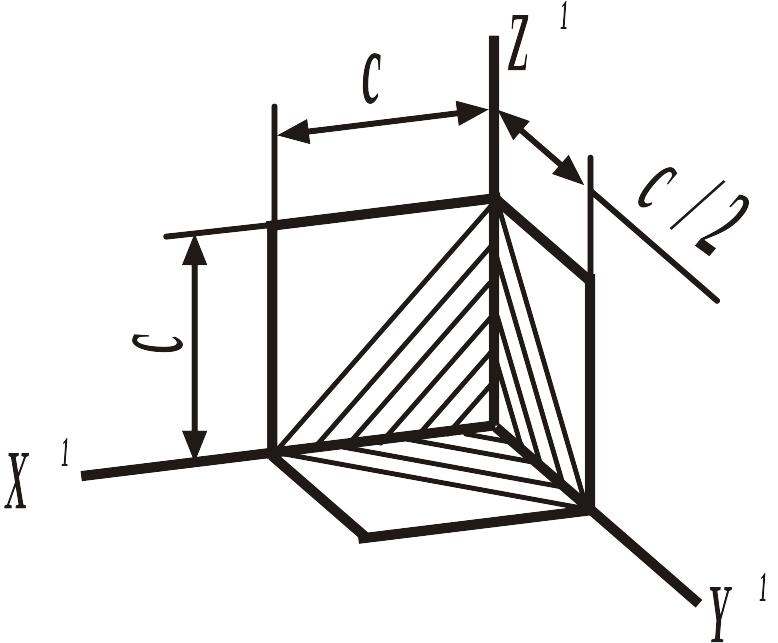
Рисунок 5.14 Рисунок 5.15

Приклад виконання креслення аксонометричних проекцій виробів за їхніми ортогональними кресленнями наведено на рис.3.11.

Побудову прямокутної диметрії зрізаного конуса виконано методом вторинних проекцій. Показано побудову точок 1 і 2 (див. рис.3.11а).

Прямокутна ізометрія деталі з подвійним проникненням наведена на рис.3.11б.

Завдання № 12. Побудова розгортки поверхонь. Виконується на форматі A3.

Приклад виконання завдання – на рис.3.12.

Необхідно накреслити наближену розгортку заданої технічної форми.

У варіантах завдання приведені технічні форми, які можна умовно розділити на три групи.

До першої відносяться технічні конструкції переходів від кругового до квадратного, від прямокутного чи квадратного перетину до кругового. Перехід складається з трикутників, основу яких складають прямокутний перетин конструкції, а протилежні вершини лежать на колі кругового перетину.

Для виконання цього завдання слід ознайомитися з методом обертання прямої відносно осі, яка перпендикулярна до площини проекції.

Побудова розгортки переходів зводиться до визначення дійсних величин трикутників і розгортанню конічних поверхонь.

До другої групи відносяться конструкції переходів від кругового перетину одного діаметра до кругового перетину іншого, розташованих у площинах, не паралельних між собою.

До третьої групи відносяться конструкції переходів від одного кругового або такого, який складається з двох півкіл, з'єднаних прямими лініями, перетину до іншого кругового перетину. Основні поверхні в цих переходах – конічні, циліндричні чи плоскі фігури.

Нижче приводиться приклад побудови розгорнення технічної форми способом тріангуляції (рис.5.16, 5.17, 5.18). Треба побудувати наближену розгортку бічної поверхні конструкції переходу від кругового до квадратного перетину (див. рис.5.16).

Аксонометричне зображення приведене на рис.5.17.

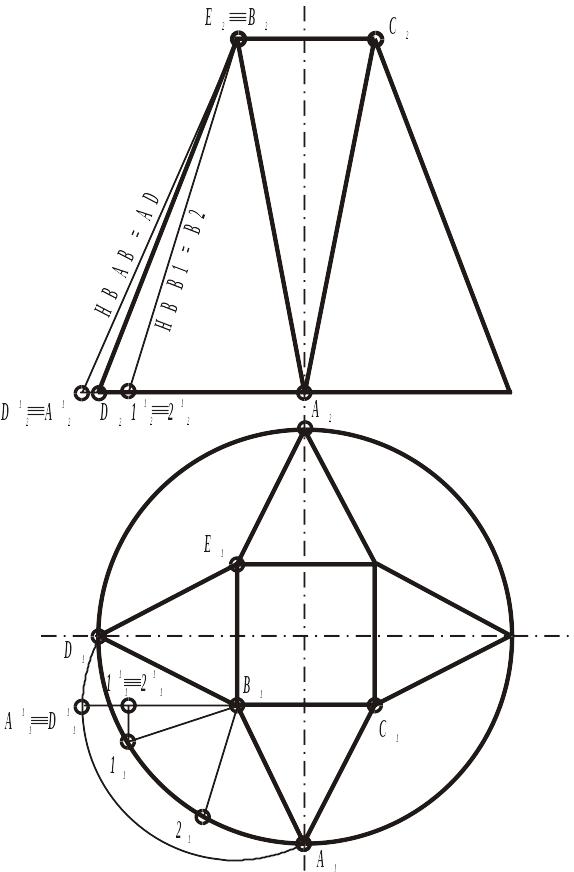
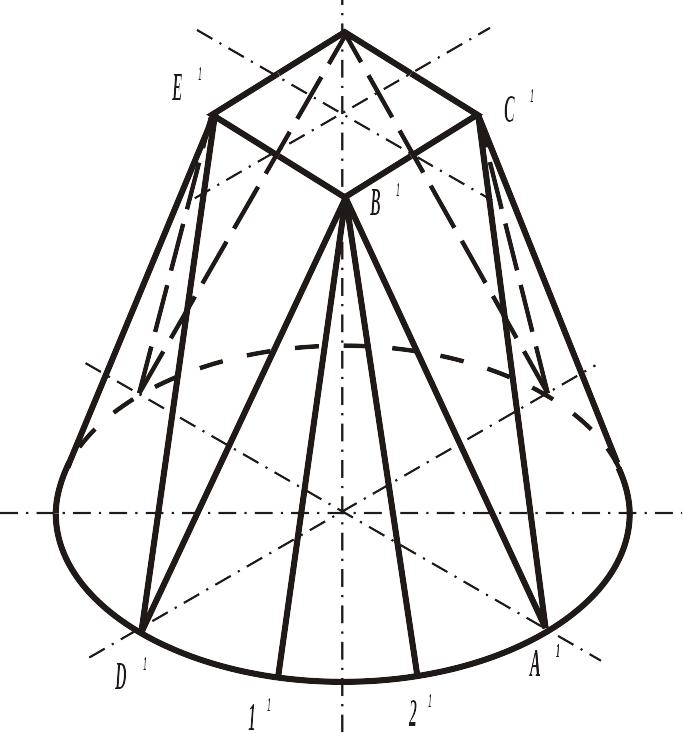
Рисунок 5.16 Рисунок 5.17

Послідовність виконання завдання може бути такий:

1. Виділити елементарні ділянки, що складають дані поверхні. Очевидно, це будуть чотири трикутники ABC(A₁B₁C₁); BDE(B₁D₁E₁);….. і чотири частини конічної поверхні ABD(A₁B₁D₁; A₂B₂D₂);…...

2. Виділену конічну поверхню, наприклад ABD, замінити вписаною пірамідальною, для чого дугу окружності AD(A₁D₁) поділяємо на три частини ˘A₁2₁; ˘2₁1₁; ˘1₁D₁. Отримані точки 1₁, 2₁ з'єднати з точкою B₁.

3. Визначити натуральні величини отриманих відрізків – AB, 2B, 1B, ВD і ін., для чого в даному випадку застосуємо метод обертання навколо осі, що є горизонтально-проектуючою, і проведеною через вершини конічних поверхонь (точки B₁, C₁…). Натуральні величини зазначених відрізків B₂A¹₂, B₂D¹₂, B₂1¹₂, B₂2¹₂ – визначені на фронтальній проекції.

4. Побудувати розгортку поверхні. Побудови 1/2 частини розгортки показана на рис.5.18 і зводиться до послідовної побудови трикутників. Так, наприклад, для побудови ΔAB2 заміряні натуральні величини його сторін |AB| = |A¹₂B|, |B2| = |B₂2¹₂|. Величина сторони |A2| дорівнює довжині дуги ˘A₁2₁, вимірити яку можна, вписавши в цю дугу ламану лінію. Всі інші побудови аналогічні розглянутим.

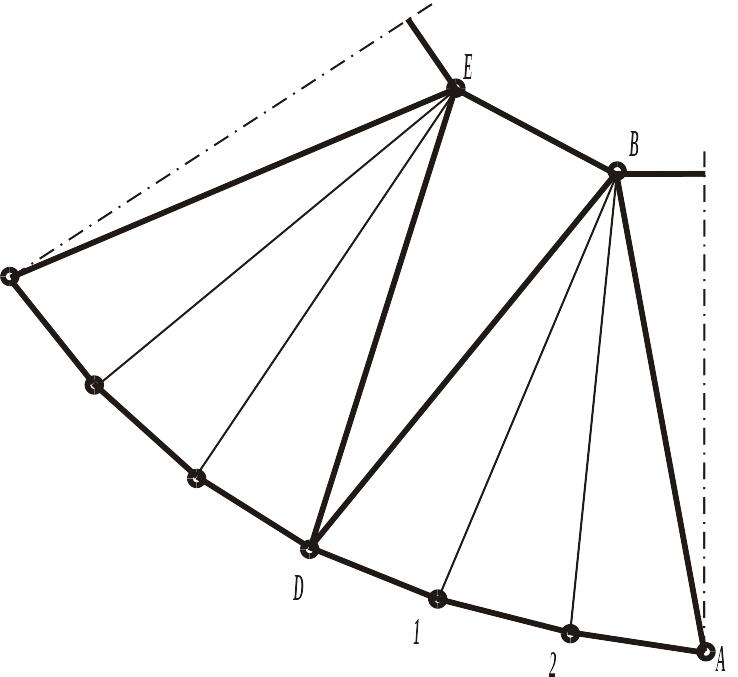
Рисунок 5.18