Вариант №31

№1. Найти матрицу обратную данной. Выполнить проверку.

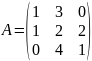
№2. Решить систему линейных уравнений по формулам Крамера. Выполнить проверку правильности решения. Решить систему методом Гаусса.

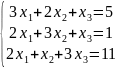
№3. Решить систему линейных уравнений.

№4. Даны координаты вершин пирамиды

.

Найти: 1) длины ребер и ; 2) угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды ; 6) канонические уравнения прямой ; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань и длину этой высоты. Для угловых величин кроме точного значения дать приближенное значение с точностью до (до одной угловой секунды). Сделать схематический рисунок с указанием всех рассматриваемых векторов.

№5. Прямые 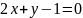и 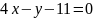являются сторонами треугольника, а точка 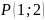- точкой пересечения третьей стороны с высотой, опущенной на нее. Составить уравнение третьей стороны треугольника. Сделать чертеж.

№6. Составить уравнение и построить линию, расстояние каждой точки которой от точки вдвое меньше расстояния от прямой .

№7. Найти пределы функций.

1)		2)
3)		4)

№8. Найти производные данных функций.

1)		2)
3)		4)

№9. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.

Вариант №32

№1. Найти матрицу обратную данной. Выполнить проверку.

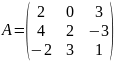
№2. Решить систему линейных уравнений по формулам Крамера. Выполнить проверку правильности решения. Решить систему методом Гаусса.

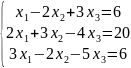
№3. Решить систему линейных уравнений.

№4. Даны координаты вершин пирамиды

.

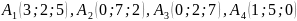Найти: 1) длины ребер и ; 2) угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды ; 6) канонические уравнения прямой ; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань и длину этой высоты. Для угловых величин кроме точного значения дать приближенное значение с точностью до (до одной угловой секунды). Сделать схематический рисунок с указанием всех рассматриваемых векторов.

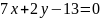№5. Прямая является одной из сторон треугольника, а прямые и его высотами. Составить уравнения двух других сторон треугольника. Сделать чертеж.

№6. Составить уравнение и построить линию, расстояние каждой точки которой от точки и от прямой относится, как 5:4.

№7. Найти пределы функций.

1)		2)
3)		4)

№8. Найти производные данных функций.

1)		2)
3)		4)

№9. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.