ТВиМС

Оглавление

1. Задачи математической статистики. Материальные объекты, их вероятностная природа. 2

2. Основные понятия выборочного метода. Точечные оценки числовых характеристик случайной величины. 2

3. Оценка плотности вероятностей и функции распределения. 2

4. Интервальное оценивание. Доверительные интервальные оценки числовых характеристик распределения. 5

5

5. Задачи структурной и параметрической идентификации. 7

8

8

6. Вероятностные модели типовых распределений. 8

9

7. Упорядочение моделей на плоскость моментов. Выбор типа модели. 10

8. Статистическое оценивание параметров модели. Метод моментов. Метод максимального правдоподобия. 11

9. Проверка статистических гипотез. Постановка задачи. Общая логическая схема проверки гипотез. Свойства критериев. 13

10. Гипотезы о равенстве дисперсий двух случайных величин (при известных и неизвестных математических ожиданиях). 15

16

11. Гипотезы о равенстве математических ожиданий двух случайных величин (при известных и неизвестных дисперсиях). 18

18

12. Критерии проверки гипотезы об однородности двух или нескольких выборок. Критерий однородности ². 19

13. Ранговый критерий однородности Вилкоксона-Манна-Уитни. 20

15. Критерии проверки гипотезы о согласии эмпирического и теоретического распределений. Критерии согласия ² – Пирсона и Колмогорова-Смирнова. Применимость критериев. 23

16. Задачи корреляционного анализа. Типы измерителей статистической связи. Постановка задачи корреляционного анализа. 27

17. Понятие тесноты статистической связи между количественными переменными. Парный коэффициент корреляции. 28

18. Проверка гипотезы о статистической значимости линейной статистической связи. Интервальная оценка парного коэффициента корреляции. 29

30

30

19. Исследование нелинейной зависимости между количественными признаками. Корреляционное отношение. 31

32

20. Проверка гипотезы об отсутствии нелинейной корреляционной связи. 32

33

21. Ранговая корреляция. Методы ранговой корреляции. 33

22. Ранговые коэффициенты корреляции Спирмена и Кендалла. 33

23. Ложная корреляция и частный коэффициент корреляции. 37

Ложная корреляция – это корреляция, которая возникла не в результате прямого соотношения между оцениваемыми переменными, а в результате их связей с третьей переменной (или четвертой, или более), при которой нет никакой связи, объединяющей эти переменные. 37

24. Множественная корреляция. Коэффициент конкордации. 38

25. Проверка гипотезы о статистической значимости выборочного коэффициента конкордации. 39

1. Задачи математической статистики. Материальные объекты, их вероятностная природа.

Математическая статистика (МС) – это часть прикладной математической дисциплины "Теория вероятностей и математическая статистика", которая изучает случайные явления, использует одинаковые с теорией вероятности методы и понятия и основана на аксиоматике /1/.

Исследование поведения объекта или явления обычно осуществляется на основе изучения статистических данных – наблюдений и измерений. Поэтому первой задачей является определение способов сбора и группировки статистической информации. Вторая задача состоит в разработке методов анализа статистических данных, адекватных целям исследования. Итак, задачи математической статистики состоят в разработке методов сбора, систематизации и обработки статистических данных для их удобного представления, интерпретации и формирования научных и практических выводов. 

Материальные объекты. Их вероятностная природа

Все законы природы и общества могут быть разбиты на несколько классов, среди которых важное местозанимают детерминированные и статистические (стохастические). Детерминированные законы – это те, для которых характерно наличие причинной обусловленности протекающих процессов. К этому классу относятся законы небесной механики, физические законы (электричество, механика и пр.), т.е. все те, которые не имеют вероятностную природу. Статистические (стохастические) законы определяют будущее состояние системы (объекта) неоднозначно, с некоторой вероятностью. Например, такие явления макромира, как долговременные изменения температуры, или явления микромира – положение электрона в электронной оболочке ("электронное облако") и др.

Можно утверждать, что без случайности нет развития. Случайностью объясняются возникновение жизни на Земле, совершенствование биологических видов, исторические события, творческая деятельность, развитие социально-экономических систем.

Именно поэтому математическая статистика становится все более значимым инструментом статистического анализа и прогнозирования состояния, поведения и развития различных систем, в том числе экономических процессов и явлений.

2. Основные понятия выборочного метода. Точечные оценки числовых характеристик случайной величины.

3. Оценка плотности вероятностей и функции распределения.

Оценивание функционных характеристик.  Оценивание функции распределения и плотности вероятностей

Пусть дана выборка из генеральной совокупности x_i,  . Необходимо получить оценку функции распределения . Положим, что x_iнезависимы. Для получения функции   выполним следующую последовательность действий:  • сформируем вариационный ряд:

х₍₁₎ ≤ х₍₂₎ ≤ …≤ х_(i) ≤ … ≤ х_(n);

• выделим минимальный х_min = х₍₁₎ и максимальный х_max = х_(n) элементы вариационного ряда;  • для каждого значения случайной величины найдем такое n_х, равное числу элементов выборки, значения которых меньше или равны заданному х. Тогда отношение

называется эмпирической функцией распределения (оценкой функции распределения).  Функция распределения, полученная по генеральной совокупности, называется истинной, или теоретической, функцией распределения и обозначается F(x).  Свойства эмпирической функции распределения:

• 0 ≤   ≤ 1, (  лежит в интервале от 0 до 1);

•  – неубывающая функция;

•  – непрерывна справа;

•  – кусочно-постоянна и изменяется только в точках вариационного ряда. В общем случае   можно представить в виде

=

0, при х х(1) ,  , при х(1) < х  х(n) ,  1, при х > х(n) ,

(3)

где n _х – количество элементов выборки, значения которых меньше или равны заданному х. В асимптотическом пределе (при  )   = F(x).

График функции   называется графиком накопленных частот.

  График накопленных частот случайной величины Х

Ломаная, соединяющая точки (х_j, n_j),  , называется полигоном частот. Ломаная, соединяющая точки (х_j, _j),   называется полигоном относительных частот. Здесь х_j – середины интервалов разбиения, а отношение

называется относительной частотой попадания в интервал.

  Полигон частот случайной величины Х

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длиной h, а высотами   (плотность частоты).

Гистограмма частот случайной величины X

Площадь j-го прямоугольника гистограммы равна,

,

а площадь всей гистограммы

S =  = n.

Функцией относительных частот (плотностью относительной частоты), или гистограммой оценки плотности вероятностей, называют фигуру, состоящую из прямоугольников с основаниями h и высотами

(4)

  Оценка плотности распределения вероятностей

Площадь j-го прямоугольника равна

,

а площадь гистограммы

 = 1.

В асимптотическом пределе

,

оценка плотности вероятности равна истинному значению плотности вероятностей.  Плотность вероятностей и функция распределения являются функционными характеристиками и дают исчерпывающие сведения об интересующем нас законе распределения случайной величины.

4. Интервальное оценивание. Доверительные интервальные оценки числовых характеристик распределения.

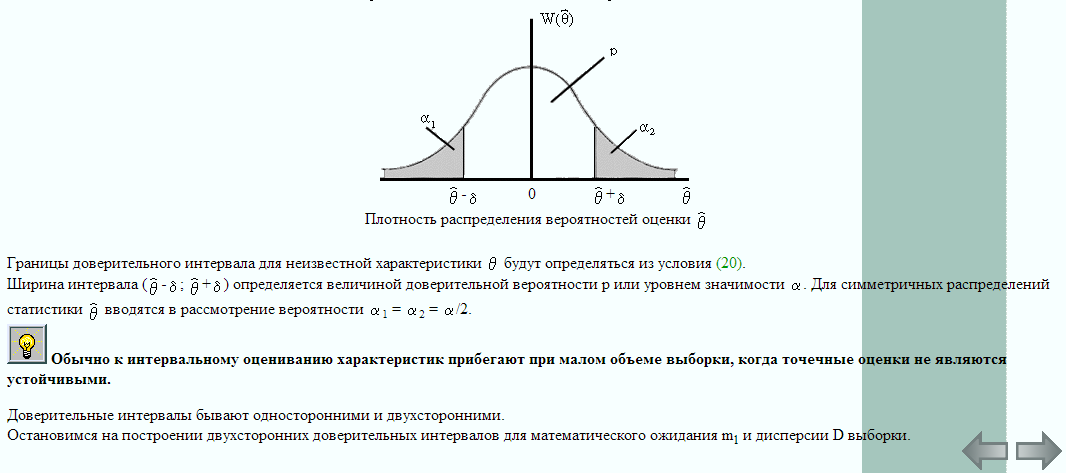
5. Задачи структурной и параметрической идентификации.

6. Вероятностные модели типовых распределений.

7. Упорядочение моделей на плоскость моментов. Выбор типа модели.

При решении прикладных статистических задач перспективным является описание исследуемого явления на модельном уровне (параметрическое описание), что требует развитых средств выбора модели из некоторым образом сформированного набора моделей.

Поскольку существует большое разнообразие моделей, то актуальным становится вопрос формирования набора моделей, из которых впоследствии будет осуществлен выбор адекватной модели. Здесь возможны два подхода:

• формирование произвольного набора моделей, например с ориентацией на прикладную область;

• формирование набора моделей по некоторому принципу (полноты, наименьшей избыточности и другое).

Выбор модели из набора можно осуществлять простым перебором моделей с последующим оцениванием параметров модели , проверкой гипотез о согласии модели и эмпирического распределения и выбором оптимальной модели в смысле минимальной критической статистики.

Другой метод выбора строится на основе предварительного упорядочения моделей по некоторым характеристикам. Рассмотрим метод упорядочения, в основе которого лежат характеристики β1^2(коэф ассиметрии случ вел) и β2(непривед коэф эксцесса) распределения случайной величины. Метод получил название метода плоскости моментов. Плоскость моментов – это плоскость в координатах b₁² и b₂. Поскольку характеристики b₁² и b₂ – случайные величины, то зона притяжения каждой модели определяется не только значениями b₁² и b₂, но и дисперсией этих характеристик. На рис приведена плоскость моментов с расположенными на ней моделями нормального, равномерного и экспоненциального распределений.

  Область недопустимых значений b ₁² и b₂ (критическая область) ограничивается соотношением b₂ ³ b₁² + 1.

Последовательность выбора модели по плоскости моментов состоит из следующих шагов:

• расположение на плоскости моментов моделей распределений в соответствии с их значениями b₁² и b₂;

• построение зоны притяжения модели (доверительных интервалов для b₁² и b₂);

• вычисление оценок   и   по выборке из генеральной совокупности и расположение точки с координатами ( ,  ) на плоскости моментов;

• выбор модели, в зону притяжения которой попала точка с координатами (  и  ).

НЕДОСТАТКИ:

• метод применим только для моделей, имеющих теоретические характеристики b₁² и b₂ ( распределение Коши, для которых теоретические моменты не существуют);

• с увеличением значений характеристик b₁² и b₂ дисперсии их оценок также увеличиваются и зоны притяжения различных моделей, расположенных на плоскости моментов, начинают перекрываться – растет неопределенность при выборе моделей;

• на плоскости моментов существует критическая область, попадание в которую   и   не позволит выбрать адекватную эмпирическим данным модель.