29) Дифференциальное уравнение свободных гармонических механических колебаний и его решение. Энергия колебаний. Физический маятник.

Энергия колебаний равна сумме кинетической и потенциальной энергий:

При гармонических колебаниях полная механическая энергия системы остаётся постоянной. При колебаниях происходит превращение кинетической энергии в потенциальную энергию, и наоборот.

30) Затухающие гармонические колебания. Коэффициент затухания и логарифмический декремент затухания. Время релаксации.

Затух. гармон. колеб.: в реальной колебательной системе действуют силы трения, которые уменьшают энергию системы. Из этого следует, что уменьшается амплитуда колебаний, т.е. колебания являются затухающими.

Коэффициент затухания (β) – физическая величина, обратная времени, в течение которого амплитуда уменьшается в e раз.

𝜒=βT=

Логарифмический декремент затухания (𝜒) – физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.

Если 𝜒=0,01, то N=100.

Время релаксации (𝜏) – это время, в течение которого амплитуда А уменьшается в e раз.

31.Вынужденные колебания. Расчёт амплитуды и фазы

Вынужденные колебания – это колебания под воздействием внешней периодической силы. Внешняя периодическая сила: совершает работу A>0, даёт поток энергии в колебательную систему(КС), не даёт колебаниям затухать, несмотря на силу трения, может изменяться во времени по различным законам.

Пусть в КС происходят линейные свободные колебания под действием упругой силы (пруж. маятник):F(x)= - kx, в системе действует .Подействуем на КС внешней силой: .Тогда уравнение 2-го закона Ньютона, учитывая силу трения и приложенную силу имеет вид: ( )

Диф. урав-ние вынужденных колебаний: ( -коэффициент затухания, -собственная частота КС.

Общее решение: Частное решение:

x=x1+x2

Определим постоянные А и ϕ. Продифференц. дважды по времени

В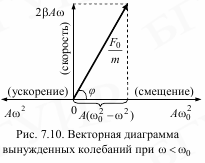 оспользуемся векторной диаграммой

Выполним действия по сложению векторов по амплитуде:

По x: Δ=

По теореме Пифагора:

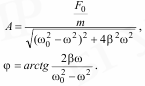
32. Резонанс механических колебаний

Резонанс - явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой к собственной частоте колебательной системы.

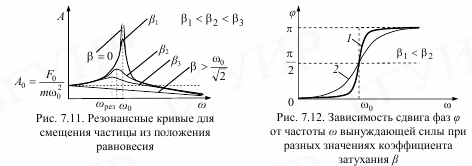
При резонансной частоте амплитуда вынужденных колебаний имеет максимум. Чем меньше β, тем больше . В случае β=0, и , что физически бессмысленно.

В реальных условиях на осциллятор всегда действуют силы сопротивления среды. При слабом затухании и значение ϕ при резонансе практически равно . Если β становится настолько большим, что , то выражение для резонансной частоты становится мнимым. Следовательно, резонанс отсутствует, амплитуда монотонно уменьшается с увеличением частоты вынуждающей силы.

При амплитуда достигает статистического отклонения - предельного значения смещения под действием постоянной силы (случай статистической деформации системы под действием постоянной силы , когда ).

При амплитуда стремится к 0. При большой частоте система не успевает колебаться и смещения относительно положения равновесия нет.

В случае малого затухания ( ) внешняя сила компенсирует в точке резонанса силу сопротивления среды, резонансная амплитуда

,где -добротность колебательной системы; - статистическое отклонение. Следовательно, чем больше , тем больше .