17. Экстремум функции двух переменных. Необходимое и достаточное условия экстремума. Нахождение наибольшего и наименьшего значений функции в замкнутой области.

Понятие максимума и минимума можно распространить и на функции нескольких переменных (здесь для случая двух переменных).

Определение. Если в некоторой окрестности точки выполняется неравенство , то говорят, что имеет максимум (минимум) в точке .

Теорема. (Необходимое условие экстремума).

Если дифференцируемая имеет экстремум в точке , то обе частные производные функции в этой точке равны нулю.

Точки, в которых обе частные производные функции обращаются в нуль, называются стационарными. Если не ограничиваться рассмотрением только дифференцируемых функций, то необходимое условие экстремума нужно дополнить.

Если имеет экстремум в точке , то:

А) или обе частные производные равны нулю в точке ;

Б) или хотя бы одна из частных производных равна бесконечности или не существует в точке .

В подозрительных точках экстремума может и не быть (сравните с функцией одной переменной).

Теорема. (Достаточные условия экстремума).

Если в критической точке выполняется неравенство , то функция имеет в точке экстремум, причем:

А) если , то минимум;

Б) если , то максимум.

Если  , то в точке нет экстремума;

Если  , то экстремум может быть и может не быть (нужны дополнительные исследования).

18. Производная сложной функции. Дифференцирование неявной функции Производная сложной функции.

Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру, 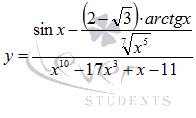смотрится очень внушительно, но сложной эта функция не является, в отличие от .

В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров.

При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами.

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а - целая рациональная функция (смотрите классификацию элементарных функций), тогда .

В свою очередь, g(x) также может быть сложной функцией. Например, . Условно такое выражение можно обозначить как . Здесь f – функция синуса, - функция извлечения квадратного корня, - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом .

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции.

Дифференцирование неявных функций

Теорема существования и дифференцируемости функции, заданной неявно

Теорема 1. Пусть функция F(x,y) удовлетворяет условиям

1. F(x0,y0) = 0 ;

2. частные производные F'x и F'y непрерывны в некоторой окрестности точки (x0,y0) ;

3. F'y(x0,y0) ≠ 0 .

Тогда

1. уравнение F(x,y) = 0 определяет неявно в некоторой окрестности точки x0 единственную непрерывную функцию y(x) , удовлетворяющую условию y(x0) = y0 .

2. функция y(x) имеет производную, непрерывную в окрестности точки x0 .

Выясним смысл условий теоремы.

Существование непрерывной неявной функции y = f(x) в окрестности точки (x0, y0) следует из теоремы существования, так как:

• условие 1 гарантирует существование точки, координаты которой удовлетворяют уравнению F(x,y) = 0 ;

• из условия 2 следует непрерывность функции F(x,y) в окрестности точки (x0,y0) , а из условия 3 — ее монотонность по y при каждом фиксированном x из этой окрестности.

Следовательно, условия 1–3 обеспечивают выполнение условий существования неявной функции y(x) , удовлетворяющей условию y(x0) = y0 и непрерывной в окрестности точки x0 .

Производная функции, заданной неявно

Функция y(x) в окрестности точки x0 обращает уравнение F(x,y) = 0 в тождество, т.е.

F(x,y(x)) ≡ 0.

Дифференцируя это тождество, получaeм dF(x, y(x)) ≡ 0, а в силу инвариантности формы полного дифференциала имеем

F'x · dx + F'y · dy(x) ≡ 0.

Отсюда получаем следующие формулы.

Дифференциал функции, заданной неявно:

dy(x) = −   F'x F'y · dx,

Производная функции, заданной неявно:

dy dx   = −   F'x F'y .

Теорема 1 обобщается для неявных функций любого числа переменных. Например:

Теорема 2. Пусть функция F(x,y,z) = 0 удовлетворяет условиям

1. F(x0,y0,z0) = 0 ;

2. частные производные F'x , F'y и F'z непрерывны в некоторой окрестности точки (x0,y0,z0) ;

3. F'z(x0,y0,z0) ≠ 0 .

Тогда

1. уравнение F(x,y,z) = 0 определяет неявно в некоторой окрестности точки (x0,y0) единственную непрерывную функцию z(x,y) , удовлетворяющую условию z(x0,y0) = z0 ;

2. функция z(x,y) имеет непрерывные частные производные в окрестности точки (x0,y0) , вычисляемые по формулам

∂z ∂x   = −   F'x F'z ,    и     ∂z ∂y   = −   F'y F'z .