15. Дифференциал функции нескольких переменных и его применение в приближенных вычислениях и для оценки погрешностей Применение дифференциала к приближенным вычислениям

Понятие дифференциала подсказывает, что если какой-Либо процесс по характеру своего изменения близок к линейному, то приращение функции мало отличается от дифференциала. Кроме того, если функция имеет конечную производную в некоторой точке х, то ее приращение и дифференциал также бесконечно малы при , стремящемся к нулю:

,

Так как дифференцируемая функция непрерывна,

Потому что произведение ограниченной функции на бесконечно малую при DX, стремящемся к нулю, есть функция бесконечно малая.

Более того, эти две бесконечно малые функции при эквивалентны:

Эквивалентность и дает возможность при малых приращениях аргумента приближенно считать

Или

Что может дать эта формула? Пусть в некоторой точке сравнительно просто вычисляются значения и . Тогда в другой точке , отстоящей недалеко от , возможно представление :

(11. 16)

Здесь остается открытым вопрос о точности получаемого результата. Это обстоятельство снижает ценность данной формулы приближенного вычисления, но в основном она полезна и широко применяется на практике.

Рассмотрим пример. В прямоугольном треугольнике катеты a=5 м и b=12 м. Какой будет гипотенуза этого треугольника, если катет a уменьшить на 0,2 м (рис. 11.5, a)?

Найдем первоначальную длину гипотенузы:

.

После уменьшения катета a на 0,2 м гипотенуза будет равна (рис. 11.5, a)

Применим теперь формулу (11.16) для приближенного нахождения с в связи с уменьшением катета a, рассматривая функцию вида:

(B=Const);

;

В обоих случаях мы получили приближенное значение искомой величины. Но в первом случае погрешность возникает в результате приближенных вычислений, а во втором, сравнительно более простом, – В связи с применением приближенной формулы (к ней также может добавиться погрешность, вызванная приближенными вычислениями). Отметим, что при уменьшении катета a На 0,2 м гипотенуза с уменьшилась примерно на 0,08 м, а полученные нами приближенные значения при этом отличаются лишь на 0,001 м.

Рассмотрим другую ситуацию: в этом же треугольнике уменьшим гипотенузу с на 0,2 м, оставив катет b без изменения (рис. 11.5, б). Определим, как в этом случае изменится катет A:

16. Уравнение касательной плоскости и нормали к поверхности

Определение: Плоскость, в которой распложены все касательные к линиям на поверхности, проходящим через точку касания M₀, называется касательной плоскостью к поверхности в точке M₀.

Определение: Нормалью к поверхности называется прямая перпендикулярная касательной плоскости и проходящая через точку касания.

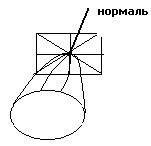Так как нормаль перпендикулярна касательной плоскости, то в качестве направляющего вектора можно взять вектор нормали к касательной плоскости (координаты вектора нормали - это частные производные.)

Тогда уравнение нормали имеет вид: ;

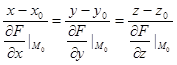То есть если уравнение поверхности задано в виде z=f(x,y), точка M₀(x₀,y₀) и f(x₀,y₀) принадлежат поверхности, точка M₀ – точка касания, тогда уравнение касательной плоскости имеет вид: .

А в случае поверхности, заданной уравнением вида F(x,y,z)=0, уравнение касательной плоскости имеет вид: 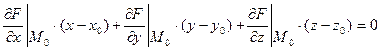, где

точка M₀(x₀,y₀,z₀) – точка касания.

 

Каноническое уравнение прямой в пространстве