
- •1.Первообразная и неопределенный интеграл, их свойства.
- •2.Табличные интегралы. Метод внесения под знак дифференциала
- •3. Замена переменной. Интегралы от иррациональных функций
- •Интегралы от иррациональных функций
- •4. Метод интегрирования по частям
- •5. Интегрирование рациональных дробей
- •6. Интегрирование тригонометрических функций
- •7. Определенный интеграл, его геометрический смысл и свойства
- •8. Формула Ньютона-Лейбница. Интегрирование по частям и замена
- •9. Несобственные интегралы, их сходимость, признаки сравнения
- •Если интегралы ограничены в совокупности, откуда и следует сходимость интеграла
- •10. Вычисление площади плоской фигуры: в декартовой, полярной системах координат; для функций, заданных параметрически
- •11. Вычисление длины дуги плоской кривой
- •13. Функция многих переменных. Область определения. График, линии и поверхности уровня
- •14. Непрерывность функции двух переменных. Частные производные. Производные высших порядков
- •Частные производные
- •15. Дифференциал функции нескольких переменных и его применение в приближенных вычислениях и для оценки погрешностей Применение дифференциала к приближенным вычислениям
- •16. Уравнение касательной плоскости и нормали к поверхности
- •17. Экстремум функции двух переменных. Необходимое и достаточное условия экстремума. Нахождение наибольшего и наименьшего значений функции в замкнутой области.
- •18. Производная сложной функции. Дифференцирование неявной функции Производная сложной функции.
- •Дифференцирование неявных функций
- •19. Производная по направлению. Градиент
- •20. Двойной интеграл, его геометрический смысл и свойства
- •21. Вычисление двойного интеграла в декартовой системе координат
- •22. Вычисление двойного интеграла в полярной системе координат
- •23. Вычисление площадей и объемов с помощью двойного интеграла
- •24. Приложение двойного интеграла в механике
- •25. Криволинейный интеграл 1-го рода, его свойства и вычисление
- •26. Масса, моменты, центр тяжести плоской кривой
- •27. Криволинейный интеграл 2-го рода, его физический смысл, свойства, вычисление и приложения
- •28. Формула Грина
- •29. Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Восстановление функции по полному дифференциалу
- •30. Числовые ряды. Сумма и сходимость числового ряда. Свойства сходящихся рядов. Ряд геометрической прогрессии
- •31. Необходимый признак сходимости числового ряда. Гармонический ряд
- •32. Признаки сравнения для рядов с положительными членами. Табличные ряды
- •37. Функциональные ряды, их область сходимости
- •38. Степенные ряды. Радиус и область сходимости степенного ряда
- •39. Ряды Тейлора и Маклорена. Нахождение коэффициентов ряда Маклорена
- •40. Разложение в ряд Маклорена функций
- •41. Применение рядов Маклорена для вычисления значений функций
- •42. Взятие неопределенных интегралов и вычисление определенных интегралов с помощью степенных рядов
14. Непрерывность функции двух переменных. Частные производные. Производные высших порядков
Определение. Число
Обозначают это так:
Все положения теории пределов функции одной переменной легко переносятся без существенных изменений на функции нескольких переменных. Определение. Пусть
Подчеркнем, что предел не
зависит от того, каким образом точка
Обозначим
Очевидно, что из непрерывности
функции двух переменных в точке
следует
непрерывность функции одной переменной
Если в какой-либо точке плоскости для нарушается условие , то функция имеет разрыв в этой точке. |
Частные производные
Пусть
![]() --
внутренняя точка области
--
внутренняя точка области
![]() ,
и в области
задана
функция
,
и в области
задана
функция
![]() .
Рассмотрим ограничение функции
на
прямую
.
Рассмотрим ограничение функции
на
прямую
![]() ,
проходящую через точку
параллельно
оси
,
проходящую через точку
параллельно
оси
![]() .
Эта прямая задаётся условиями
.
Эта прямая задаётся условиями
![]() при
при
![]() ;
переменная
;
переменная
![]() может
при этом произвольно меняться. Поэтому
для рассматриваемого ограничения
может
при этом произвольно меняться. Поэтому
для рассматриваемого ограничения
![]() имеется
естественная параметризация, смысл
которой в том, что "замораживаются"
все переменные, от которых зависит
имеется
естественная параметризация, смысл
которой в том, что "замораживаются"
все переменные, от которых зависит
![]() ,
кроме
:
,
кроме
:
![]()
Получили функцию одного переменного
![]() ,
как параметризацию ограничения с помощью
параметра
.
,
как параметризацию ограничения с помощью
параметра
.
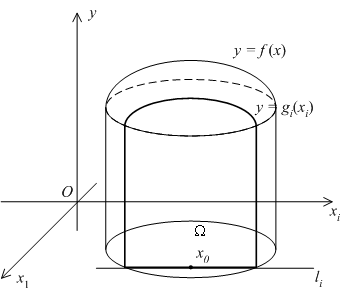
Рис.7.12.
Функция
может
иметь производную в точке
![]() ,
равную некоторому числу
,
равную некоторому числу
![]() .
Это число называют частной производной
функции
по
переменной
,
вычисленной в точке
.
Эта частная производная обозначается
.
Это число называют частной производной
функции
по
переменной
,
вычисленной в точке
.
Эта частная производная обозначается
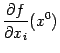 или
или
![]() .
.
Сразу же заметим, что значения
частных производных от функции
в
точке
,
вычисленные по разным переменным
и
![]() ,
могут быть различными, так что обозначение
типа
,
могут быть различными, так что обозначение
типа
![]() ,
без указания переменной, по которой
вычислена частная производная, не имеет
смысла: в обозначении обязательно нужно
указывать переменную, по которой мы
дифференцируем.
,
без указания переменной, по которой
вычислена частная производная, не имеет
смысла: в обозначении обязательно нужно
указывать переменную, по которой мы
дифференцируем.
Итак, чтобы вычислить частную производную от функции по некоторой переменной , нужно фиксировать значения всех переменных, кроме (то есть временно считать их постоянными), а затем по обычным правилам вычисления производных найти производную по этой единственной переменной . Теперь ясно, что для вычисления частных производных никаких новых правил дифференцирования вдобавок к тем, что известны нам для функций одной переменной, не потребуется, ведь при вычислении частной производной мы считаем, что может изменяться только одна переменная.
Считая точку
![]() ,
в которой вычисляется значение частной
производной
,
переменной точкой области
и
предполагая, что во всех точках
эта
производная существует, мы получаем,
что частная производная
,
в которой вычисляется значение частной
производной
,
переменной точкой области
и
предполагая, что во всех точках
эта
производная существует, мы получаем,
что частная производная
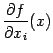 --
это функция, заданная в области
(или
в её части, если производная существует
не везде в
).
--
это функция, заданная в области
(или
в её части, если производная существует
не везде в
).
Поскольку частную производную
функции
можно
вычислять по каждой из
![]() переменных
переменных
![]() ,
то функция
имеет
частных
производных
,
то функция
имеет
частных
производных
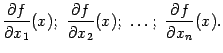
Эти частные производные, вообще говоря, -- различные функции. Их называют также частными производными первого порядка от функции . Итак, функция переменных имеет частных производных первого порядка.
Производные высшего порядка явно заданной функции
Пусть функция y = f(x) имеет конечную производную f '(x) в некотором интервале (a, b), т.е. производная f '(x) также является функцией в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции f, которая обозначается в виде
![]()
Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:
![]()
Производные более высокого порядка (если они существуют) определяются как
![]()
Таким образом, понятие производной n-го порядка вводится индуктивно путем последовательного вычисления n производных, начиная с производной первого порядка. Переход к производной следующего, более высокого порядка производится с помощью рекуррентной формулы
![]()
В ряде случаев можно вывести общую формулу для производной произвольного n-го порядка без вычисления промежуточных производных. Некоторые такие примеры рассмотрены ниже. Отметим, что для нахождения производных высшего порядка можно использовать следующие линейные соотношения:
![]()
Производные высшего порядка неявно заданной функции
Производная n-го порядка неявно заданной функции находится последовательным (n раз) дифференцированием уравнения F(x, y) = 0. На каждом шаге, после соответствующих подстановок и преобразований, можно получить явное выражение для производной, зависящее лишь от переменных x, y, т.е. производные имеют вид
![]()
Производные высшего порядка функции, заданной параметрически
Рассмотрим функцию y = f(x), заданную параметрически с помощью двух уравнений
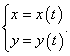
Первая производная данной функции выражается формулой
![]()
Дифференцируя еще раз по x, находим производную второго порядка:
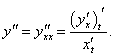
Аналогично определяются производные третьего и более высокого порядка:


 .
.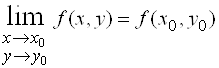 ,
то функция
называется
непрерывной в точке
,
то функция
называется
непрерывной в точке