
- •1.Первообразная и неопределенный интеграл, их свойства.
- •2.Табличные интегралы. Метод внесения под знак дифференциала
- •3. Замена переменной. Интегралы от иррациональных функций
- •Интегралы от иррациональных функций
- •4. Метод интегрирования по частям
- •5. Интегрирование рациональных дробей
- •6. Интегрирование тригонометрических функций
- •7. Определенный интеграл, его геометрический смысл и свойства
- •8. Формула Ньютона-Лейбница. Интегрирование по частям и замена
- •9. Несобственные интегралы, их сходимость, признаки сравнения
- •Если интегралы ограничены в совокупности, откуда и следует сходимость интеграла
- •10. Вычисление площади плоской фигуры: в декартовой, полярной системах координат; для функций, заданных параметрически
- •11. Вычисление длины дуги плоской кривой
- •13. Функция многих переменных. Область определения. График, линии и поверхности уровня
- •14. Непрерывность функции двух переменных. Частные производные. Производные высших порядков
- •Частные производные
- •15. Дифференциал функции нескольких переменных и его применение в приближенных вычислениях и для оценки погрешностей Применение дифференциала к приближенным вычислениям
- •16. Уравнение касательной плоскости и нормали к поверхности
- •17. Экстремум функции двух переменных. Необходимое и достаточное условия экстремума. Нахождение наибольшего и наименьшего значений функции в замкнутой области.
- •18. Производная сложной функции. Дифференцирование неявной функции Производная сложной функции.
- •Дифференцирование неявных функций
- •19. Производная по направлению. Градиент
- •20. Двойной интеграл, его геометрический смысл и свойства
- •21. Вычисление двойного интеграла в декартовой системе координат
- •22. Вычисление двойного интеграла в полярной системе координат
- •23. Вычисление площадей и объемов с помощью двойного интеграла
- •24. Приложение двойного интеграла в механике
- •25. Криволинейный интеграл 1-го рода, его свойства и вычисление
- •26. Масса, моменты, центр тяжести плоской кривой
- •27. Криволинейный интеграл 2-го рода, его физический смысл, свойства, вычисление и приложения
- •28. Формула Грина
- •29. Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Восстановление функции по полному дифференциалу
- •30. Числовые ряды. Сумма и сходимость числового ряда. Свойства сходящихся рядов. Ряд геометрической прогрессии
- •31. Необходимый признак сходимости числового ряда. Гармонический ряд
- •32. Признаки сравнения для рядов с положительными членами. Табличные ряды
- •37. Функциональные ряды, их область сходимости
- •38. Степенные ряды. Радиус и область сходимости степенного ряда
- •39. Ряды Тейлора и Маклорена. Нахождение коэффициентов ряда Маклорена
- •40. Разложение в ряд Маклорена функций
- •41. Применение рядов Маклорена для вычисления значений функций
- •42. Взятие неопределенных интегралов и вычисление определенных интегралов с помощью степенных рядов
Если интегралы ограничены в совокупности, откуда и следует сходимость интеграла
Частный признак сравнения.
Если при
![]() функция
функция
![]() является
бесконечно малой порядка
является
бесконечно малой порядка
![]() >0
по сравнению с
>0
по сравнению с
![]() ,
то интеграл
сходится
при
>1
и расходится при
,
то интеграл
сходится
при
>1
и расходится при
![]() .
.
Функция
![]() называется
бесконечно малой n-го
порядка по сравнению с
называется
бесконечно малой n-го
порядка по сравнению с
![]() при
при
![]() ,
если
,
если
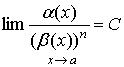 ,
где 0<
,
где 0<![]() <
<
10. Вычисление площади плоской фигуры: в декартовой, полярной системах координат; для функций, заданных параметрически



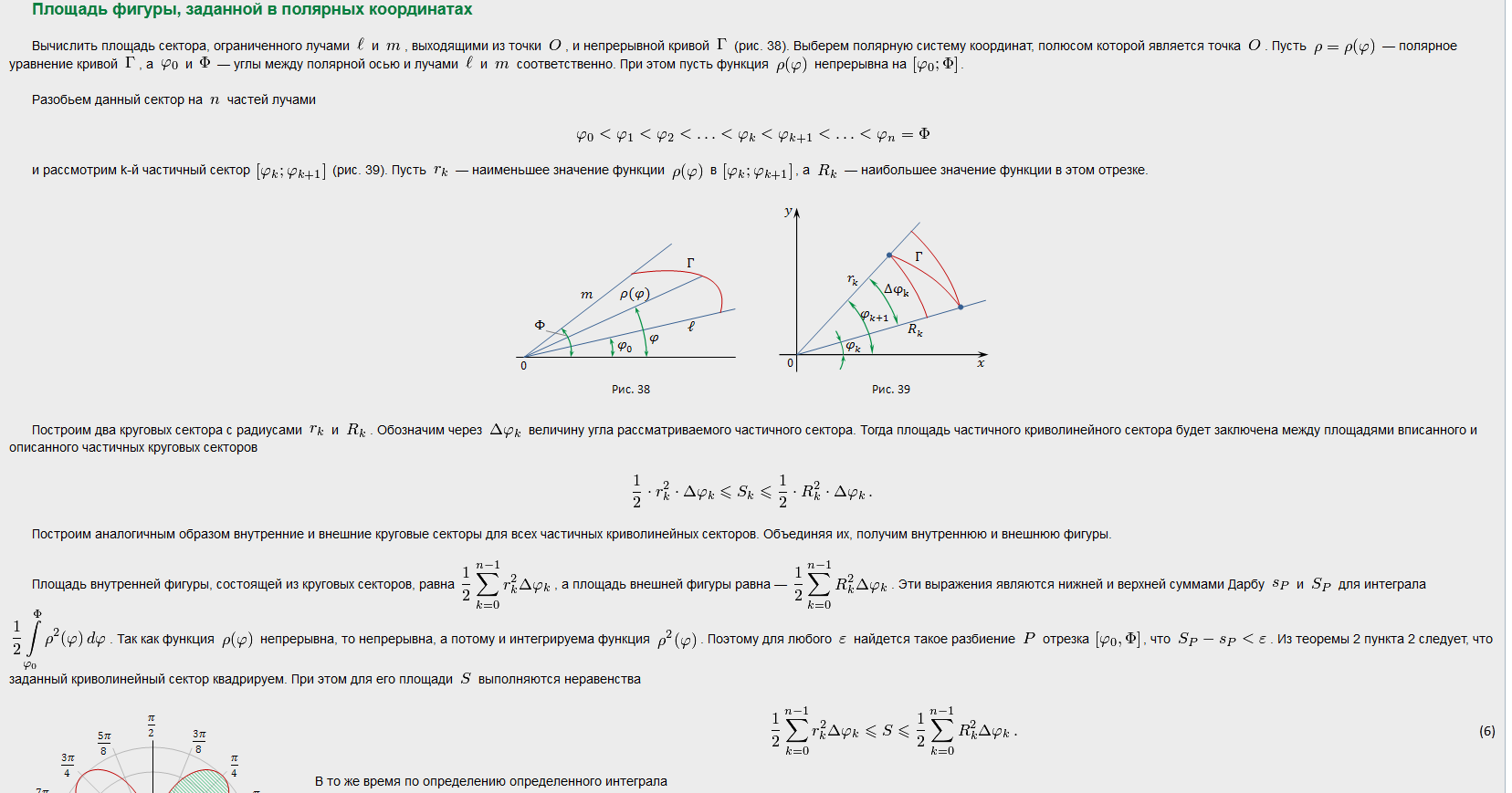

11. Вычисление длины дуги плоской кривой
Пусть кривая
![]() ,
заданная уравнением
,
заданная уравнением
![]() ,
где
,
где
![]() ,
лежит в плоскости
,
лежит в плоскости
![]() (Рис.
14).
(Рис.
14).

Рис. 14
Определение. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
1. Для кривой, заданной уравнением
![]() ,
,
![]()
Если функция
и
ее производная
![]() непрерывны
на отрезке
непрерывны
на отрезке
![]() ,
то длина дуги кривой
вычисляется
по формуле
,
то длина дуги кривой
вычисляется
по формуле
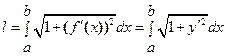 .
(13)
.
(13)
12. Вычисление объемов тел вращения
|
Пусть требуется вычислить объем
тела, образованного вращением вокруг
оси Ох фигуры, ограниченной линиями:
|
С помощью произвольно выбранных
точек
![]() разобьем
отрезок
разобьем
отрезок
![]() на
n элементарных отрезков длиной
на
n элементарных отрезков длиной
![]() i
= 1, 2, …, n. Через точки деления проведем
плоскости перпендикулярно оси Ох.
Получим n элементарных объемов тел
вращения. На каждом элементарном отрезке
выберем произвольно точку
i
= 1, 2, …, n. Через точки деления проведем
плоскости перпендикулярно оси Ох.
Получим n элементарных объемов тел
вращения. На каждом элементарном отрезке
выберем произвольно точку
![]() и
вычислим значение функции
и
вычислим значение функции
![]() .
Каждое элементарное тело вращения
заменим цилиндром с радиусом основания
и
высотой
.
Каждое элементарное тело вращения
заменим цилиндром с радиусом основания
и
высотой
![]() ,
объем которого равен
,
объем которого равен
![]() .
Объем всего тела вращения приближенно
равен
.
Объем всего тела вращения приближенно
равен
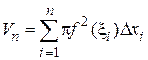 .
.
Данная сумма является
интегральной. Перейдем к пределу при
![]() ,
,
![]() и
получим точное значение объема
и
получим точное значение объема
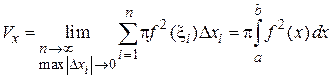
или
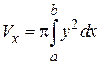 .
.
Если тело образуется вращением
вокруг оси Оy фигуры, ограниченной
линиями:
![]() ,
,
![]() ,
то его объем находится по формуле
,
то его объем находится по формуле
 .
.
13. Функция многих переменных. Область определения. График, линии и поверхности уровня
Определение 16.1. Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у из некоторой области их изменения D соответствует определенное значение величины z, то говорят, что z является функцией от x и y в области D.
Символически функция двух переменных обозначается так:
![]() .
.
Как и функция одной переменной она может быть задана аналитически, таблично и графически. Переход от одного способа задания к другому осуществляется по тем же правилам, что и для функции одной переменной.
Пусть функция задана формулой
![]() .
Составим для нее таблицу значений, в
первой строке которой будут находиться
значения х, а в первом столбце –
значения у. Выберем произвольные
значения для х и у, а z
получается согласно заданному правилу.
.
Составим для нее таблицу значений, в
первой строке которой будут находиться
значения х, а в первом столбце –
значения у. Выберем произвольные
значения для х и у, а z
получается согласно заданному правилу.
x y |
0,1 |
0,2 |
0,3 |
0,4 |
|
0,2 |
0,4 |
0,6 |
0,8 |
|
1,2 |
1,4 |
1,6 |
1,8 |
|
2,2 |
2,4 |
2,6 |
2,8 |
|
3,2 |
3,4 |
3,6 |
3,8 |
|
4,2 |
4,4 |
4,6 |
4,8 |
Для того чтобы построить график этой функции нужно из каждой точки М(х,у) плоскости ХОY поднять перпендикуляр z и потом объединить полученные точки аппликат. Следует учесть, что графическое изображение функции двух переменных в трехмерном декартовом базисе в общем случае представляет некоторую поверхность. В лекции 8 мы показывали, что построение линии «по точкам» страдает приближенностью и даже ошибочностью, потому что не может учесть такие важные точки, как разрывы, экстремумы и т.д. Поэтому если надо построить график поверхности, решают вопрос в общем виде, определив ее тип, а потом переходят к построению.
Если на плоскости самая простая и самая изученная линия – это прямая, то наиболее простая поверхность в пространстве – это плоскость, уравнение которой в общем виде записывается так:
![]() .
(16.1)
.
(16.1)
Разделив обе части равенства на D, получим равносильное уравнение
![]() ,
(16.2)
,
(16.2)
где
![]()
![]() ,
,
![]() .
Его называют уравнением плоскости «в
отрезках».
.
Его называют уравнением плоскости «в
отрезках».
По полученному уравнению (16.2)
легко изобразить плоскость в декартовой
системе координат. Найдем точки ее
пересечения с осями координат: с осью
ОХ :
![]() ,
,
![]()
![]() ,
с осью ОY:
,
с осью ОY:
![]() ,
,
![]() ,
и с осью ОZ:
,
,
и с осью ОZ:
,
![]() .
Соединим полученные точки, продолжая
их во все стороны, и получим изображение
плоскости.
.
Соединим полученные точки, продолжая
их во все стороны, и получим изображение
плоскости.
Для нашего случая
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Построим эту плоскость по точкам
.
Построим эту плоскость по точкам
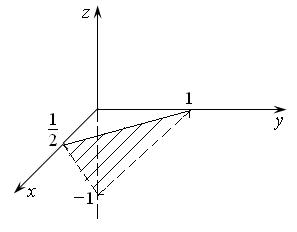
Рис. 16.1
В разделе «Аналитическая геометрия» мы также изучили кривые второго порядка – окружность, эллипс, гиперболу и параболу. В трехмерном пространстве они перешли в сферу, эллипсоид, гиперболоид (однополостный и двуполостный) и параболоид. В сечении этих тел плоскостями, параллельными координатным плоскостям, получаются все те же окружность, эллипс и т.д. Но на этом дело не закончилось. Кривые, вырвавшись в трехмерное пространство, создали эллиптический гиперболоид, гиперболический параболоид, конические и цилиндрические поверхности. Перечень поверхностей второго порядка и их графики приведены в приложении 1. Вглядитесь в их уравнения и постарайтесь понять логику их названий.
Как и в случае одной переменной, функция двух переменных существует не при любых значениях х и у.
Определение 16.2. Совокупность
пар значений (х, у), при которых
определяется функция
![]() ,
называется областью определения
или областью существования этой
функции.
,
называется областью определения
или областью существования этой
функции.
Область определения наглядно
иллюстрируется геометрически, как
совокупность точек, принадлежащих
плоскости ХОY. Именно она называется
областью определения функции. В
дальнейшем мы будем рассматривать
области, ограниченные некоторыми
линиями. Эти линии называются границами
области. Точки, не лежащие на границе,
называют внутренними точками
области. Область, состоящая только из
внутренних точек, называется незамкнутой,
или открытой. Если к области относятся
и точки границы, то ее называют замкнутой.
Область называется ограниченной,
если существует такое положительное
число С, что расстояние любой точки
![]() плоскости
от начала координат О(0,0) меньше С,
т.е.
плоскости
от начала координат О(0,0) меньше С,
т.е.
![]() .
.
Пример 16.1. Найти
область определения функции
![]() .
.
Решение. Для того чтобы z имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е. х и у должны удовлетворять неравенству
![]() ,
или
,
или
![]() .
.
Все точки, удовлетворяющие этому неравенству, лежат в круге радиуса 1 с центром в начале координат и на границе этого круга (рис. 16.2).
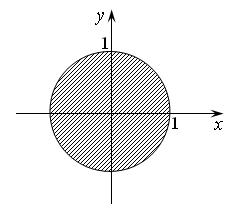
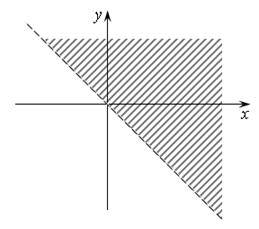
Рис. 16.2 Рис. 16.3

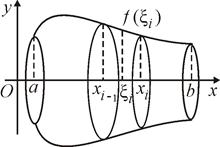 Рис.
67
Рис.
67