5. Интегрирование рациональных дробей
Теорема 6. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором ее знаменатель не равен нулю, существует и выражается через элементарные функции, а именно рациональные дроби, логарифмы и арктангенсы.
Доказательство.
Представим
рациональную дробь
в виде:
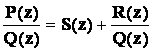. При этом последнее слагаемое является
правильной дробью, и по теореме 5 ее
можно представить в виде линейной
комбинации простейших дробей. Таким
образом, интегрирование рациональной
дроби сводится к интегрированию
многочлена S(x)
и простейших дробей, первообразные
которых, как было показано, имеют вид,
указанный в теореме.
Замечание. Основную трудность при этом составляет разложение знаменателя на множители, то есть поиск всех его корней.
Пример
1. Найти интеграл
Подынтегральная
функция является правильной рациональной
дробью. Разложение на неприводимые
сомножители знаменателя имеет вид
Это означает, что разложение подынтегральной
функции в сумму простейших дробей имеет
следующий вид:
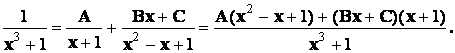
Найдем коэффициенты разложения комбинированным методом:
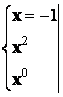
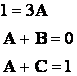
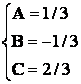
Таким образом,
Пример
2. Найти интеграл
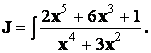
Подынтегральная функция – неправильная дробь, поэтому выделяем целую часть:
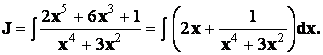
Первый из интегралов – табличный, а второй вычислим разложением правильной дроби на простейшие:
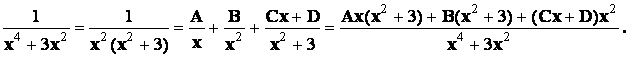
Имеем по методу неопределенных коэффициентов:
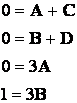
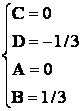
Таким образом,
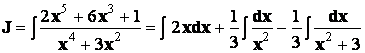
6. Интегрирование тригонометрических функций
Множество задач сводится к нахождению интегралов трансцендентных функций, содержащих тригонометрические функции. В данной статье сгруппируем наиболее часто встречающиеся виды подынтегральных функций и на примерах рассмотрим методы их интегрирования.
Начнем с интегрирования синуса, косинуса, тангенса и котангенса.
Из таблицы
первообразных сразу заметим, что
и
.
Метод
подведения под знак дифференциала
позволяет вычислить неопределенные
интегралы функций тангенса и котангенса:
К началу страницы
Поясним, как были найдены формулы
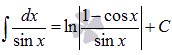и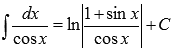
,
находящиеся в таблице первообразных.
Разберем первый случай, второй абсолютно аналогичен.
Воспользуемся
методом
подстановки:
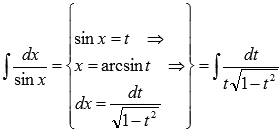
Пришли к задаче
интегрирования
иррациональной функции. Здесь
нам также поможет метод подстановки:
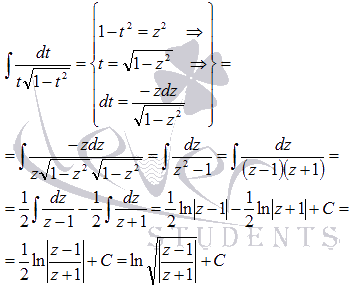
Осталось провести
обратную замену
и
t = sinx:
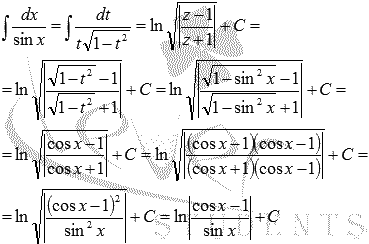
К началу страницы
Отдельно хочется остановиться на интегралах, содержащих степени тригонометрических функций, вида
.
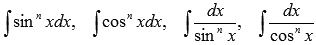Подробно о
принципах их нахождении можете
ознакомиться в разделе интегрирование
с использованием рекуррентных формул.
Если изучите вывод этих формул, то без
особого труда сможете брать интегралы
вида
,
где m и n – натуральные числа.
К началу страницы
Когда тригонометрические функции идут в комбинациях с многочленами или показательными функциями, то применяется метод интегрирования по частям.этом разделе даны рекомендации для нахождения интегралов
,
.
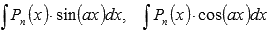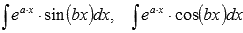К началу страницы
Максимум творчества приходится вкладывать, когда подынтегральная функция содержит тригонометрические функции с различными аргументами.
Здесь на помощь приходят основные формулы тригонометрии. Так что выписывайте их на отдельный листочек и держите перед глазами.