37. Функциональные ряды, их область сходимости

Ряд    членами которого являются функции, называется функциональным рядом.

Совокупность тех значений  x,  при которых функциональный ряд сходится, называется областью сходимости ряда.

В области сходимости его сумма является функцией от  x,  поэтому сумму функционального ряда обозначают  S(x) .

Наибольшее использование в технике имеют степенные ряды и ряды Фурье.

38. Степенные ряды. Радиус и область сходимости степенного ряда

Функциональный ряд вида:

называется степенным рядом. Постоянные числа  a₀, a₁, a₂, ..., a_n...  называются коэффициентами ряда. Постоянное число  x₀  называется центром ряда.

Областью сходимости степенного ряда является интервал  ,  который называется интервалом сходимости степенного ряда, число R называется радиусом сходимости. На интервале сходимости степенной ряд сходится абсолютно, при    степенной ряд расходится.

При  x = R, x = -R   вопрос о сходимости степенного ряда решается индивидуально для каждого конкретного ряда. Внутри интервала сходимости степенные ряды можно почленно дифференцировать и интегрировать.

Радиус сходимости определяется следующими пределами:

39. Ряды Тейлора и Маклорена. Нахождение коэффициентов ряда Маклорена

Функция  f(x)  называется аналитической в точке  x₀,  если в некоторой окрестности числа  x₀  функция  f(x)  является суммой степенного ряда

,

который называется рядом Тейлора функции  f(x). 

В частном случае, при x = 0 ряд Тейлора называется рядом Маклорена:

,

Ряды Тейлора и Маклорена можно использовать для нахождения приближенных значений аналитической функции.

40. Разложение в ряд Маклорена функций

41. Применение рядов Маклорена для вычисления значений функций

Найти число с максимальной степенью точности, составляющей 0,001.

Здесь необходимо разложение в ряд Маклорена (30.10). В данном случае, если , то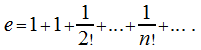 Поскольку из (30.9)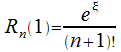 , а , то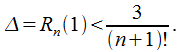

В случае, когда получаем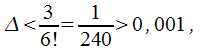 если же , то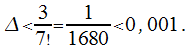

Следовательно .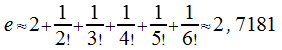

Предположим, что необходимо найти разлагается на ряд Тейлора (30.6). В этом случае возможно осуществление почленно интегрирования внутри интервала сходимости. Определенный интеграл находят с заданной степенью точности.

Пример: Найти интеграл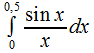 с максимальной точностью, составляющей 0, 001.

На основе разложения (30.12) запишем:

 

 

Учитывая то, что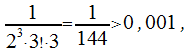 а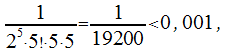 то в соответствии с признаком Лейбница имеем

 

.

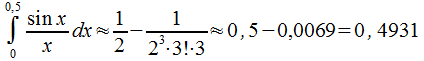42. Взятие неопределенных интегралов и вычисление определенных интегралов с помощью степенных рядов

Если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости этого ряда, то соответствующий определенный интеграл можно вычислить с заданной точностью.

Пример 32.6; Вычислить интеграл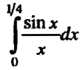 С точностью до о, ooooi.

Разделив почленно ряд для sin* нал, получим

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем

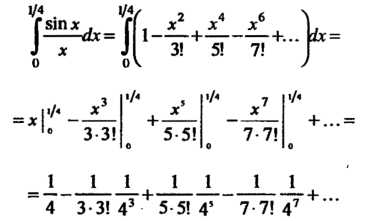
Ограничиваясь первыми двумя членами этого ряда, находим

Погрешность не превзойдет первого отброшенного члена:

Пример 32.7 Вычислить интеграл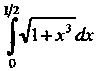 С точностью до

Подынтегральная функция разлагается в степенной ряд

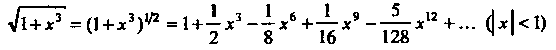
Интегрируя этот ряд почленно в промежутке , находим

Поскольку То для вычисления данного интеграла

С указанной точностью достаточно взять два первых члена полученного ряда, т. е.