28. Формула Грина

Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция

с непрерывными частными производными первого порядка 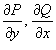. Тогда справедлива формула Грина

где символ указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если , то формула Грина принимает вид

где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией

Ротором или вихрем векторного поля называется вектор, обозначаемый или и равный

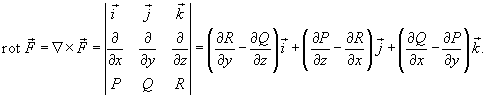
Формула Грина в векторной форме записывается в виде

Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.

29. Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Восстановление функции по полному дифференциалу

Криволинейный интеграл второго рода от векторной функции не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция , такая, что

В этом случае криволинейный интеграл второго рода от функции вдоль кривой C от точки A до точки B выражается формулой

(Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение

Векторное поле, обладающее свойством , называется потенциальным, а функция называется потенциалом.

Признак потенциальности поля

Криволинейный интеграл II рода от функции не зависит от пути интегрирования, если

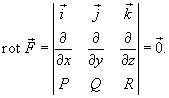
Предполагается, что каждый компонент функции имеет непрерывные частные производные по переменным x, y и z. Если криволинейный интеграл рассматривается в плоскости Oxy, то в случае потенциального поля будет справедливо соотношение

В этом случае признак потенциальности векторного поля упрощается и принимает вид

Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна.

30. Числовые ряды. Сумма и сходимость числового ряда. Свойства сходящихся рядов. Ряд геометрической прогрессии

Пусть мы имеем числовую последовательность , где .

Приведем пример числовой последовательности: .

Числовой ряд – это сумма членов числовой последовательности вида .

В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: .

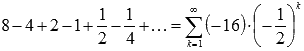называют общим членом числового ряда или k–ым членом ряда.

Для предыдущего примера общий член числового ряда имеет вид .

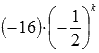Частичная сумма числового ряда – это сумма вида , где n – некоторое натуральное число. называют также n-ой частичной суммой числового ряда.

К примеру, четвертая частичная сумма ряда есть .

Частичные суммы образуют бесконечную последовательность частичных сумм числового ряда.

Для нашего ряда n –ая частичная сумма находится по формуле суммы первых n членов геометрической прогрессии 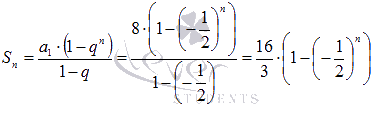, то есть, будем иметь следующую последовательность частичных сумм: .

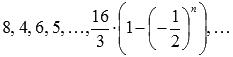Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.

Суммой сходящегося числового ряда называется предел последовательности его частичных сумм, то есть, .

В нашем примере , следовательно, ряд сходится, причем его сумма равна шестнадцати третьим: .

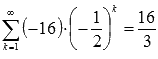В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица: . n–ая частичная сумма определяется выражением 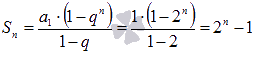, а предел частичных сумм бесконечен: .

Еще одним примером расходящегося числового ряда является сумма вида . В этом случае n–ая частичная сумма может быть вычислена как . Предел частичных сумм бесконечен .

 СУММА ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ВИДА СО ЗНАМЕНАТЕЛЕМ q ЯВЛЯЕТСЯ СХОДЯЩИМСЯ ЧИСЛОВЫМ РЯДОМ, ЕСЛИ , И РАСХОДЯЩИМСЯ РЯДОМ ПРИ .

Докажем это.

Мы знаем, что сумма первых n членов геометрической прогрессии находится по формуле .

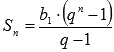При справедливо 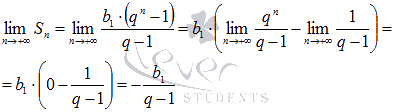что указывает на сходимость числового ряда.

При q = 1 имеем числовой ряд . Его частичные суммы находятся как , а предел частичных сумм бесконечен , что указывает на расходимость ряда в этом случае.

Если q = -1, то числовой ряд примет вид 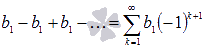. Частичные суммы принимают значение для нечетных n, и для четных n. Из этого можно сделать вывод, что предел частичных сумм не существует и ряд расходится.

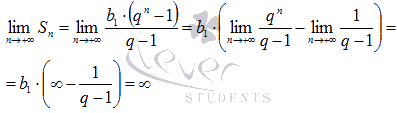При справедливо что указывает на расходимость числового ряда.