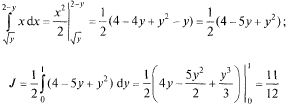- •1.Первообразная и неопределенный интеграл, их свойства.
- •2.Табличные интегралы. Метод внесения под знак дифференциала
- •3. Замена переменной. Интегралы от иррациональных функций
- •Интегралы от иррациональных функций
- •4. Метод интегрирования по частям
- •5. Интегрирование рациональных дробей
- •6. Интегрирование тригонометрических функций
- •7. Определенный интеграл, его геометрический смысл и свойства
- •8. Формула Ньютона-Лейбница. Интегрирование по частям и замена
- •9. Несобственные интегралы, их сходимость, признаки сравнения
- •Если интегралы ограничены в совокупности, откуда и следует сходимость интеграла
- •10. Вычисление площади плоской фигуры: в декартовой, полярной системах координат; для функций, заданных параметрически
- •11. Вычисление длины дуги плоской кривой
- •13. Функция многих переменных. Область определения. График, линии и поверхности уровня
- •14. Непрерывность функции двух переменных. Частные производные. Производные высших порядков
- •Частные производные
- •15. Дифференциал функции нескольких переменных и его применение в приближенных вычислениях и для оценки погрешностей Применение дифференциала к приближенным вычислениям
- •16. Уравнение касательной плоскости и нормали к поверхности
- •17. Экстремум функции двух переменных. Необходимое и достаточное условия экстремума. Нахождение наибольшего и наименьшего значений функции в замкнутой области.
- •18. Производная сложной функции. Дифференцирование неявной функции Производная сложной функции.
- •Дифференцирование неявных функций
- •19. Производная по направлению. Градиент
- •20. Двойной интеграл, его геометрический смысл и свойства
- •21. Вычисление двойного интеграла в декартовой системе координат
- •22. Вычисление двойного интеграла в полярной системе координат
- •23. Вычисление площадей и объемов с помощью двойного интеграла
- •24. Приложение двойного интеграла в механике
- •25. Криволинейный интеграл 1-го рода, его свойства и вычисление
- •26. Масса, моменты, центр тяжести плоской кривой
- •27. Криволинейный интеграл 2-го рода, его физический смысл, свойства, вычисление и приложения
- •28. Формула Грина
- •29. Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Восстановление функции по полному дифференциалу
- •30. Числовые ряды. Сумма и сходимость числового ряда. Свойства сходящихся рядов. Ряд геометрической прогрессии
- •31. Необходимый признак сходимости числового ряда. Гармонический ряд
- •32. Признаки сравнения для рядов с положительными членами. Табличные ряды
- •37. Функциональные ряды, их область сходимости
- •38. Степенные ряды. Радиус и область сходимости степенного ряда
- •39. Ряды Тейлора и Маклорена. Нахождение коэффициентов ряда Маклорена
- •40. Разложение в ряд Маклорена функций
- •41. Применение рядов Маклорена для вычисления значений функций
- •42. Взятие неопределенных интегралов и вычисление определенных интегралов с помощью степенных рядов
20. Двойной интеграл, его геометрический смысл и свойства
Если
![]() в
D, то двойной интеграл от функции
в
D, то двойной интеграл от функции
![]() по
области D равен объему тела,
ограниченного поверхностью
по
области D равен объему тела,
ограниченного поверхностью
![]() ,
,
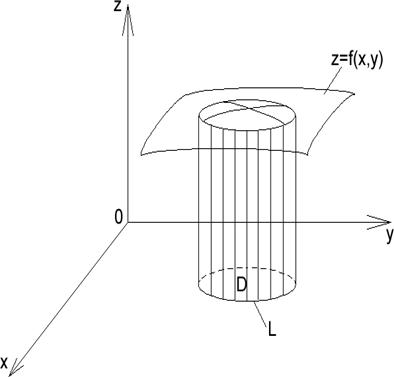
Рис. 5
плоскостью XOY и цилиндрической поверхностью, образующая которой параллельна оси OZ, а направляющей является линия L – граница области D (рис. 5).
Из такого представления двойного
интеграла следует, что двойной интеграл
есть число, которое зависит только от
вида подынтегральной функции
![]() и
от положения и вида области интегрирования.
и
от положения и вида области интегрирования.
21. Вычисление двойного интеграла в декартовой системе координат
О: Область D называется правильной в направлении оси OY (ОХ), если любая прямая, параллельная оси OY(OX) и проходящая через внутреннюю точку области Д пересекает ее границу в двух точках.
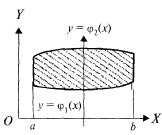
Рис. 23.3
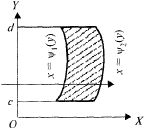
Рис. 23.4
Граница области D, правильной
в направлении оси OY (рис. 23.3), может быть
задана уравнениями![]()
![]() и
двойной интеграл в этом случае вычисляется
по формуле
и
двойной интеграл в этом случае вычисляется
по формуле
![]() (23.5)
(23.5)
причем сначала вычисляется
внутренний интеграл![]()
в котором х считается постоянной. Выражение справа в (23.5) называется повторным, или двукратным интегралом.
Граница области D, правильной
в направлении оси ОХ (рис. 23.4), может быть
задана уравнениями:![]()
![]() Тогда
двойной интеграл вычисляется по формуле
Тогда
двойной интеграл вычисляется по формуле
![]() (23.6)
(23.6)
Если область D правильная в направлении ОХ и OY (правильная область), то применимы обе формулы.
Рассмотрим геометрический смысл формулы (23.5), для формулы (23.6) рассуждения аналогичные (вывод формул приведен в [6. С. 310]).
Предположим, что![]() и
граница области D является правильной
в направлении оси OY.
и
граница области D является правильной
в направлении оси OY.
Из разд. 23.1![]()
Подсчитаем теперь объем V методом поперечных сечений (см. п.18.2.1):
![]() (23.7)
(23.7)
Проводя через т. (х,0,0) плоскость
перпендикулярно оси ОХ, получим в сечении
криволинейную трапецию![]()
(рис. 23.5), с площадью![]()
для точек линии![]() при
постоянном х зависит только от у:
при
постоянном х зависит только от у:
![]() -
(23.8)
-
(23.8)
площадь поперечного сечения цилиндрического тела. Подставляя (23.8) в (23.7), получаем
![]()
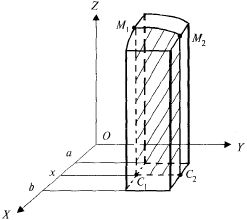
Рис. 23.5
Таким образом, в формуле (23.7) слева и справа имеем объем цилиндрического тела.
Формулы (23.5) и (23.6) выведены в предположении, что область имеет специальный вид.
В общем случае область D разбивают на конечное число частей, являющихся правильными, и вычисляют для каждой из частей интеграл по формуле (23.5) или (23.6). Интеграл по всей области (свойство 3°) равен сумме полученных интегралов.
Если область ГУ.![]() то
формулы (23.5) и (23.6)
то
формулы (23.5) и (23.6)
примут вид
![]()
Пример:![]()
Решение разбивается на три этапа:
1) построение области D;
2) переход к повторному интегралу, расстановка пределов интегрирован ия;
3) вычисление повторного интеграла.
Решая систему![]() находим
т. пересечения параболы
находим
т. пересечения параболы
и прямой (1, 1), (-2, 4). Строим
область, (-2, 4)![]() D
(рис. 23.6). Так как область правильная, то
можно воспользоваться формулами (23.5) и
(23.6).
D
(рис. 23.6). Так как область правильная, то
можно воспользоваться формулами (23.5) и
(23.6).
При решении по (23.5) область придется разбить на две: ОВС и СВА, так как линия ОБА задается разными уравнениями:
![]()
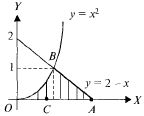
Рис. 23.6
При вычислении по формуле
(23.6) приходим к одному повторному
интегралу![]() Закончим
Закончим
решение, пользуясь последней формулой: