
- •1.Первообразная и неопределенный интеграл, их свойства.
- •2.Табличные интегралы. Метод внесения под знак дифференциала
- •3. Замена переменной. Интегралы от иррациональных функций
- •Интегралы от иррациональных функций
- •4. Метод интегрирования по частям
- •5. Интегрирование рациональных дробей
- •6. Интегрирование тригонометрических функций
- •7. Определенный интеграл, его геометрический смысл и свойства
- •8. Формула Ньютона-Лейбница. Интегрирование по частям и замена
- •9. Несобственные интегралы, их сходимость, признаки сравнения
- •Если интегралы ограничены в совокупности, откуда и следует сходимость интеграла
- •10. Вычисление площади плоской фигуры: в декартовой, полярной системах координат; для функций, заданных параметрически
- •11. Вычисление длины дуги плоской кривой
- •13. Функция многих переменных. Область определения. График, линии и поверхности уровня
- •14. Непрерывность функции двух переменных. Частные производные. Производные высших порядков
- •Частные производные
- •15. Дифференциал функции нескольких переменных и его применение в приближенных вычислениях и для оценки погрешностей Применение дифференциала к приближенным вычислениям
- •16. Уравнение касательной плоскости и нормали к поверхности
- •17. Экстремум функции двух переменных. Необходимое и достаточное условия экстремума. Нахождение наибольшего и наименьшего значений функции в замкнутой области.
- •18. Производная сложной функции. Дифференцирование неявной функции Производная сложной функции.
- •Дифференцирование неявных функций
- •19. Производная по направлению. Градиент
- •20. Двойной интеграл, его геометрический смысл и свойства
- •21. Вычисление двойного интеграла в декартовой системе координат
- •22. Вычисление двойного интеграла в полярной системе координат
- •23. Вычисление площадей и объемов с помощью двойного интеграла
- •24. Приложение двойного интеграла в механике
- •25. Криволинейный интеграл 1-го рода, его свойства и вычисление
- •26. Масса, моменты, центр тяжести плоской кривой
- •27. Криволинейный интеграл 2-го рода, его физический смысл, свойства, вычисление и приложения
- •28. Формула Грина
- •29. Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Восстановление функции по полному дифференциалу
- •30. Числовые ряды. Сумма и сходимость числового ряда. Свойства сходящихся рядов. Ряд геометрической прогрессии
- •31. Необходимый признак сходимости числового ряда. Гармонический ряд
- •32. Признаки сравнения для рядов с положительными членами. Табличные ряды
- •37. Функциональные ряды, их область сходимости
- •38. Степенные ряды. Радиус и область сходимости степенного ряда
- •39. Ряды Тейлора и Маклорена. Нахождение коэффициентов ряда Маклорена
- •40. Разложение в ряд Маклорена функций
- •41. Применение рядов Маклорена для вычисления значений функций
- •42. Взятие неопределенных интегралов и вычисление определенных интегралов с помощью степенных рядов
1.Первообразная и неопределенный интеграл, их свойства.
Определение первообразной.
Первообразной
функции f(x)
на промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство
![]() для
любого х
из заданного промежутка.
для
любого х
из заданного промежутка.
Если
принять во внимание тот факт, что
производная от константы С
равна нулю, то справедливо равенство
![]() .
Таким образом, функция f(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
.
Таким образом, функция f(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение неопределенного интеграла.
Все
множество первообразных функции f(x)
называется неопределенным интегралом
этой функции и обозначается
![]() .
.
Выражение
![]() называют
подынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
называют
подынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
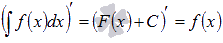 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции.
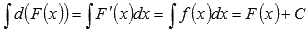 Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
 ,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
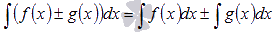 Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для
доказательства третьего и четвертого
свойств достаточно найти производные
от правых частей равенств:
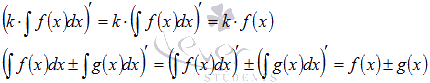
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
2.Табличные интегралы. Метод внесения под знак дифференциала

Сначала немного поговорим о постановке задачи в общем виде, а затем перейдём к примерам интегрирования подстановкой. Допустим, в нас есть некий интеграл ∫g(x)dx. Однако в таблице интегралов нужной формулы нет, да и разбить заданный интеграл на несколько табличных не удаётся (т.е. непосредственное интегрирование отпадает). Однако задача будет решена, если нам удастся найти некую подстановку u=φ(x), которая сведёт наш интеграл ∫g(x)dx к какому-либо табличному интегралу ∫f(u)du=F(u)+C. После применения формулы ∫f(u)du=F(u)+C нам останется только вернуть обратно переменную x. Формально это можно записать так:
∫g(x)dx=|u=φ(x)|=∫f(u)du=F(u)+C=F(φ(x))+C.
Проблема в том, как выбрать такую подстановку u. Для этого понадобится знание, во-первых, таблицы производных и умение её применять для дифференцирования сложных функций, а во-вторых, таблицы неопределенных интегралов. Кроме того, нам будет крайне необходима формула, которую я запишу ниже. Если y=f(x), то:
dy=y′dx(1)
Т.е. дифференциал некоторой функции равен производной этой функции, умноженной на дифференциал независимой переменной. Это правило очень важно, и именно оно позволит применять метод подстановки. Здесь же укажем пару частных случаев, которые получаются из формулы (1). Пусть y=x+C, где C – некая константа (число, попросту говоря). Тогда, подставляя в формулу (1) вместо y выражение x+C, получим следующее:
d(x+C)=(x+C)′dx
Так как (x+C)′=x′+C′=1+0=1, то указанная выше формула станет такой:
d(x+C)=(x+C)′dx=1⋅dx=dx.
Запишем полученный результат отдельно, т.е.
dx=d(x+C)(2)
Полученная формула означает, что прибавление константы под дифференциалом не изменяет оный дифференциал, т.е. dx=d(x+10), dx=d(x−587) и так далее.
Рассмотрим еще один частный случай для формулы (1). Пусть y=Cx, где C, опять-таки, является некоторой константой. Найдем дифференциал этой функции, подставляя в формулу (1) выражение Cx вместо y:
d(Cx)=(Cx)′dx
Так как (Cx)′=C⋅(x)′=C⋅1=C, то записанная выше формула d(Cx)=(Cx)′dx станет такой: d(Cx)=Cdx. Если разделить обе части этой формулы на C (при условии C≠0), то получим d(Cx)C=dx. Этот результат можно переписать в несколько иной форме:
dx=1C⋅d(Cx)(C≠0)(3)
Полученная формула говорит о том, что умножение выражения под дифференциалом на некую ненулевую константу требует введения соответствующего множителя, компенсирующего такое домножение. Например, dx=15d(5x), dx=−119d(19x).
В примерах №1 и №2 формулы (2) и (3) будут рассмотрены подробно.
Замечание относительно формул
В данной теме будут использоваться как формулы 1-3, так и формулы из таблицы неопределённых интегралов, которые тоже имеют свои номера. Чтобы не было путаницы, условимся о следующем: если в теме встречается текст "используем формулу №1", то означает он буквально следующее "используем формулу №1, расположенную на этой странице". Если нам понадобится формула из таблицы интегралов, то это будем оговаривать каждый раз отдельно. Например, так: "используем формулу №1 из таблицы интегралов".
И ещё одно небольшое примечание
Перед началом работы с примерами рекомендуется ознакомиться с материалом, изложенным в предыдущих темах, посвящённых понятию неопределённого интеграла и непосредственному интегрированию. Изложение материала в этой теме опирается на сведения, указанные в упомянутых темах.
