
- •Гипотеза Планка
- •Виды фотоэлектрического эффекта.Законы внешнего фотоэффекта
- •§ 203. Уравнение Эйнштейна для внешнего фотоэффекта. Экспериментальное подтверждение квантовых свойств света
- •История открытия
- •Внешний фотоэффект
- •Законы внешнего фотоэффекта
- •Теория Фаулера
- •Квантовый выход
- •Внутренний фотоэффект
- •Вентильный фотоэффект
- •Фотовольтаический эффект
- •Ядерный фотоэффект
- •Современные исследования
- •Коэффициент полезного действия
- •Другие похожие показатели
- •Кпд котлов
- •Тепловые насосы и холодильные машины
- •Формулировка
- •[Править] Следствия [править] Недостижимость абсолютного нуля температур
- •[Править] Поведение термодинамических коэффициентов
- •[Править] Нарушения третьего начала термодинамики в моделях
- •Принцип действия тепловой машины. Коэффициент полезного действия тепловых машин
- •[Править]Обратный эффект Комптона
- •Нульмерные дефекты
- •[Править]Термодинамика точечных дефектов
- •[Править]Миграция точечных дефектов
- •[Править]Источники и стоки точечных дефектов
- •Комплексы точечных дефектов
- •Одномерные дефекты
- •Двумерные дефекты]
- •Трёхмерные дефекты
- •Методы избавления от дефектов
- •Полезные дефекты
- •Постулаты Бора
- •§4 Опыты Франка и Герца
- •Спектр атома водорода по Бору
- •Собственная и примесная проводимость полупроводников
- •Физическая природа
- •Применение
- •Основное уравнение мкт
- •Вывод основного уравнения мкт
- •Уравнение среднеквадратичной скорости молекулы
- •Давление газа
- •Состояние физической системы
- •Примеры
- •Обобщённые координаты
- •Примеры
- •Степени свободы в статистической физике и термодинамике
- •Вымораживание степеней свободы
- •Степени свободы молекулы
- •Формулировка
- •Изобарный процесс
- •Изохорный процесс
- •Изотермический процесс
- •Изоэнтропийный процесс
- •1.Статистический и термодинамический методы
- •2.Молекулярно-кинетическая теория идеальных газов
- •2.1.Основные определения
- •2.2.Опытные законы идеального газа
- •2.3.Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
- •2.5.Распределение Максвелла
- •2.6.Распределение Больцмана
- •3.Термодинамика
- •3.1.Внутренняя энергия. Закон равномерного распределения энергии по степеням свободы
[Править] Нарушения третьего начала термодинамики в моделях
Третье начало термодинамики часто нарушается в модельных системах. Так, при энтропия классического идеального газа стремится к минус бесконечности. Это говорит о том, что при низких температурах уравнение Менделеева — Клапейрона неадекватно описывает поведение реальных газов.
Таким образом, третье начало термодинамики указывает на недостаточность классической механики и статистики и является макроскопическим проявлением квантовых свойств реальных систем.
В квантовой механике, тем не менее, в модельных системах третье начало также может нарушаться. Таковы все случаи, когда применяется распределение Гиббса и основное состояние является вырожденным.
Несоблюдение третьего начала в модели, однако, не исключает того, что в каком-то диапазоне изменения физических величин эта модель может быть вполне адекватна.
Принцип действия тепловой машины. Коэффициент полезного действия тепловых машин

Большая часть двигателей на Земле - это тепловые двигатели. Устройства, превращающие энергию топлива в механическую энергию, называются тепловыми двигателями. Любой тепловой двигатель (паровые и газовые турбины, двигатели внутреннего сгорания) состоит из трех основных элементов:рабочего тела (это газ), которое совершает работу в двигателе; нагревателя, от которого рабочее тело получает энергию, часть которой затем идет на совершение работы; холодильника, которым является атмосфера или специальные устройства.
Ни один тепловой двигатель не может работать при одинаковой температуре его рабочего тела и окружающей среды. Обязательно температура нагревателя больше температуры холодильника. При совершении работы тепловыми двигателями происходит передача теплоты от более горячих тел к более холодным. Рабочее тело двигателя получает количество теплоты QН от нагревателя, совершает работу A' и передает холодильнику количество теплоты Q<subХ< sub=""></subХ<>. В соответствии с законом сохранения энергии А' < QН - QХ. В случае равенства речь идет об идеальном двигателе, в котором нет потерь энергии.
Отношение
работы к энергии, которое получило
рабочее тело от нагревателя, называют
коэффициентом полезного действия
(КПД):![]() <
1.
<
1.
В процессе работы многочисленных тепловых машин возникают тепловые потери, которые в конечном счете приводят к повышению внутренней энергии атмосферы, т. е. к повышению ее температуры. Это может привести к таянию ледников и катастрофическому повышению уровня Мирового океана, а вместе с тем к глобальному изменению природных условий. При работе тепловых установок и двигателей в атмосферу выбрасываются вредные для человека, животных и растений оксиды азота, углерода и серы. С вредными последствиями работы тепловых машин можно бороться путем повышения КПД, их регулировки и создания новых двигателей, не выбрасывающих вредные вещества с отработанными газами.
Фотоэффект |
|
Фотоэффектом называется испускание электронов с поверхности металла под действием света. В 1888 г. Г. Герц обнаружил, что при облучении ультрафиолетовыми лучами электродов, находящихся под высоким напряжением, разряд возникает при большем расстоянии между электродами, чем без облучения. |
|
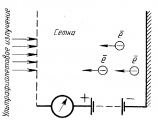
Фотоэффект можно наблюдать в следующих случаях: 1. Цинковую пластину, соединенную с электроскопом, заряжают отрицательно и облучают ультрафиолетовым светом. Она быстро разряжается. Если же ее зарядить положительно, то заряд пластины не изменится. |
|
2. Ультрафиолетовые лучи, проходящие через сетчатый положительныйэлектрод, попадают на отрицательно заряженную цинковую пластину и выбивают из нее электроны, которые устремляются к сетке, создавая фототек, регистрируемый чувствительным гальванометром. |
|
Законы фотоэффекта Количественные закономерности фотоэффекта (1888—1889) были установлены А. Г. Столетовым. |
|
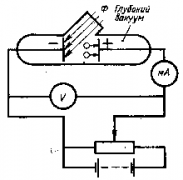
Он использовал вакуумный стеклянный баллон с двумя электродами. Через кварцевое стекло на катод попадает свет (в том числе ультрафиолетовое излучение). С помощью потенциометра можно регулировать напряжение между электродами. Ток в цепи измерялся миллиамперметром. |
|
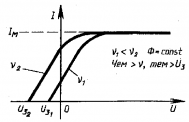
В результате облучения электроны, выбитые из электрода, могут достигнуть противоположного электрода и создать некоторый начальный ток. При увеличении напряжения, поле разгоняет электроны, и ток увеличивается, достигая насыщения, при котором все выбитые электроны достигают анода. Если
приложить обратное напряжение, то
электроны тормозятся и ток уменьшается.
При так называемом запирающем
напряжении фототок
прекращается. Согласно закону
сохранения энергии |
|
Важнейшим свойством фотоэффекта является его безынерционность,которая не может быть объяснена с точки зрения волной теории. |
|
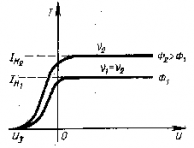
Первый закон Исследуя зависимость силы тока в баллоне от напряжения между электродами при постоянном световом потоке на один из них, он установил первый закон фотоэффекта. Фототок насыщения пропорционален световому потоку, падающему на металл. Т.к. сила тока определяется величиной заряда, а световой поток - энергией светового пучка, то можно сказать: число электронов, выбиваемых за 1 с из вещества, пропорционально интенсивности света, падающего на это вещество. |
|
Второй закон Изменяя условия освещения на этой же установке, А. Г. Столетовоткрыл второй закон фотоэффекта: кинетическая энергия фотоэлектронов не зависит от интенсивности падающего света, а зависит от его частоты. Из опыта следовало, что если частоту света увеличить, то при неизменном световом потоке запирающее напряжение увеличивается, а, следовательно, увеличивается и кинетическая энергия фотоэлектронов. Таким образом, кинетическая энергия фотоэлектронов линейно возрастает с частотой света. |
|
Третий закон Заменяя в приборе материал фотокатода, Столетов установил третий закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, т. е. существует наименьшая частота nmin, при которой еще возможен фотоэффект. При n < nmin ни
при какой интенсивности волны падающего
на фотокатод света фотоэффект не
произойдет. Т.к. |
|
Теория фотоэффекта А. Эйнштейн, развив идею М. Планка (1905), показал, что законы фотоэффекта могут быть объяснены при помощи квантовой теории. Явление фотоэффекта экспериментально доказывает: свет имеет прерывистую структуру. Излученная порция E=hv сохраняет свою индивидуальность и поглощается веществом только целиком. |
|
Эйнштейн предположил: 1. Один фотон может выбить только один электрон (это верно для всех процессов с небольшой интенсивностью излучения). 2. На основании закона сохранения энергии:
Его смысл: энергия кванта тратится на работу выхода электрона из металла и сообщение электрону кинетической энергии. |
|
В этом уравнении: ν - частота падающего света, m - масса электрона (фотоэлектрона), υ - скорость электрона, h - постоянная Планка, A - работа выхода электронов из металла. |
|
Работа выхода - это характеристика материала (табличная величина). Она показывает, какую работу должен совершить электрон, чтобы преодолеть поверхностную разность потенциалов и выйти за пределы металла. Работа выхода обычно измеряется в электронвольтах (эВ). |
|
Доказательство законов фотоэффекта 1.
Число фотонов Nф равно
числу электронов Nэ.
Энергия света 2.
Из уравнения Эйнштейна: 3.
Минимальная частота света соответствует
Ек=0,
то |
|
Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.
Цикл Карно назван в честь французского военного инженера Сади Карно, который впервые его исследовал в 1824 году.
Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этомэнтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.
[править]Описание цикла Карно
Цикл Карно в координатах P и V
Цикл Карно в координатах T и S
Пусть тепловая
машина состоит
из нагревателя с температурой ![]() ,
холодильника с температурой
,
холодильника с температурой ![]() и рабочего
тела.
и рабочего
тела.
Цикл Карно состоит из четырёх стадий:
Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты
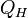 .
При этом объём рабочего тела увеличивается.
.
При этом объём рабочего тела увеличивается.Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру , приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты
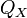 .
.Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.
При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:
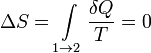 при
при ![]() .
.
Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).
[править]КПД тепловой машины Карно
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
![]() .
.
Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику
![]() .
.
Отсюда коэффициент полезного действия тепловой машины Карно равен
![]() .
.
Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равнаабсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Поэтому максимальный КПД любой тепловой машины будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлинга равен КПД цикла Карно.
[править]Связь между обратимостью цикла и КПД
Для того, чтобы цикл был обратимым, из него должна быть исключена передача теплоты при наличии разности температур (так как такие процессы необратимы в силу постулата Томсона). Значит, передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того, чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.
Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: вдвигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД.
Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше чем КПД цикла Карно.
Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие упругого рассеивания егоэлектронами. Обнаружен американским физиком Артуром Комптоном в 1923 году для рентгеновского излучения. В 1927 Комптон получил за это открытие Нобелевскую премию по физике.
Иллюстрация к эффекту Комптона
При
рассеянии фотона на
покоящемся электроне частоты
фотона
и ![]() (до
и после рассеяния соответственно)
связаны соотношением:
(до
и после рассеяния соответственно)
связаны соотношением:
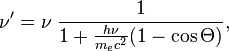
где ![]() —
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
—
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
Перейдя к длинам волн:
![]()
где ![]() — комптоновская
длина волны электрона.
— комптоновская
длина волны электрона.
Для электрона ![]() м.
Уменьшение энергии фотона после
комптоновского рассеяния
называется комптоновским
сдвигом.
В классической электродинамике рассеяние
электромагнитной волны на заряде
(томсоновское
рассеяние)
не сопровождается уменьшением её
частоты.
м.
Уменьшение энергии фотона после
комптоновского рассеяния
называется комптоновским
сдвигом.
В классической электродинамике рассеяние
электромагнитной волны на заряде
(томсоновское
рассеяние)
не сопровождается уменьшением её
частоты.
Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волнаявляется непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.



 ,
где m- масса электрона, а υmax -
максимальная скорость фотоэлектрона.
,
где m- масса электрона, а υmax -
максимальная скорость фотоэлектрона.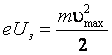

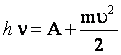 -
уравнение Эйнштейна.
-
уравнение Эйнштейна.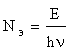 .
.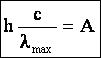 .
.