3.Термодинамика

3.1.Внутренняя энергия. Закон равномерного распределения энергии по степеням свободы

Внутренняя энергия U - энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.Внутренняя энергия - однозначная функция термодинамического состояния системы, т.е. в каждом состоянии система обладает вполне определенной (единственной) энергией. Внутренняя энергия не зависит от того, как система пришла в данное состояние: при переходе из состояния (1) в состояние (2) изменение внутренней энергии DU определяется только разностью значений внутренней энергии этих состояний DU = U₁ - U₂  и не зависит от пути перехода.

Число степеней свободы системы i - это число независимых переменных (координат), полностью определяющих положение системы в пространстве:

- Одноатомная молекула идеального газа имеет три степени свободы поступательного движения, т.е. i=3.

- Двухатомная молекула идеального газа имеет три степени поступательного движения и две степени свободы вращательного движения, т.е. i=5.

- Трехатомная молекула (и вообще нелинейная многоатомная молекула) идеального газа имеет три степени поступательного движения и три степени вращательного движения, т.е. i=6.

- Для реальных молекул следует учитывать также степени свободы колебательного движения.

- Независимо от числа степеней свободы молекул три степени свободы всегда поступательные; ни одна из поступательных степеней свободы не имеет преимущества перед остальными.

Закон Больцмана о равномерном распределении энергии по степеням свободы молекул:

для системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень - в среднем энергия, равная kT (на колебательную степень свободы приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы). Таким образом, средняя энергия молекулы Е> = ikT/2, где i -   сумма числа поступательных i_пост, числа вращательных i_вращ и удвоенного числа колебательных i_колеб степеней свободы молекулы i = i_пост + i_вращ + 2i_колеб. Для идеального газа i совпадает с числом степеней свободы молекулы.

Внутренняя энергия 1 моль идеального газа равна сумме кинетических энергий N_A молекул

U_m = ikTN_A = iRT/2, (1a)

и изменение внутренней энергии 1 моль идеального газа dU_m =(iR/2)dT (1b)

(молекулы между собой не взаимодействуют и поэтому взаимная потенциальная энергия молекул газа равна нулю).

Внутренняя энергия произвольной массы m идеального газа U = (m/M)(iRT/2)=n(iRT/2), где М - молярная масса (масса одного моля), n = m/M - количество вещества.

Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплотыδQ, полученного телом, к соответствующему приращению его температуры δT:

Единица измерения теплоёмкости в системе СИ — Дж/К.

Удельная теплоёмкость

Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.

Массовая теплоёмкость (С) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг⁻¹·К⁻¹).

Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м⁻³·К⁻¹).

Молярная теплоёмкость (С_μ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)).

Теплоёмкость для различных состояний вещества

Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).

Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна:

где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная.

А при постоянном давлении

Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К).

Теория теплоёмкости

Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела

Существует несколько теорий теплоёмкости твердого тела:

• Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).

• Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.

• Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.

Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц.

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости  , предельными частными явлениями политропного процесса являются изотермический процесс ( ) и адиабатный процесс ( ).

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными ^?.

Показатель политропы

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

где р — давление, V — объем газа, n — «показатель политропы».

. Здесь   — теплоёмкость газа в данном процессе,   и   — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс: 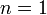 , так как  , значит, по закону Бойля — Мариотта  , и уравнение политропы вынуждено выглядеть так:  .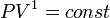

• Изобарный процесс: 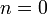 , так как  , и уравнение политропы вынуждено выглядеть так:  .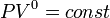

• Адиабатный процесс: 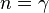  (здесь   — показатель адиабаты), это следует из уравнения Пуассона.

• Изохорный процесс: 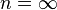 , так как  , и в процессе 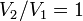 , а из уравнения политропы следует, что 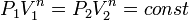 , то есть, что  , то есть 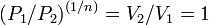 , а это возможно, только если   является бесконечным.

Термодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия), совпадают.

Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу.

Компонентами любой тепловой машины являются рабочее тело, нагреватель и холодильник (с помощью которых меняется состояние рабочего тела).

Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропиясистемы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, цикл Стирлинга ицикл Эрикссона), в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора. Общим (т.е. указанные циклы частный случай) для всех этих циклов с регенерацией является Цикл Рейтлингера. Можно показать (см. статью Цикл Карно), что обратимые циклы обладают наибольшей эффективностью.

Основные принципы

Прямое преобразование тепловой энергии в работу запрещается постулатом Томсона (см. Второе начало термодинамики). Поэтому для этой цели используются термодинамические циклы.

Для того, чтобы управлять состоянием рабочего тела, в тепловую машину входят нагреватель и холодильник. В каждом цикле рабочее тело забирает некоторое количество теплоты ( ) у нагревателя и отдаёт количество теплоты   холодильнику. Работа, совершённая тепловой машиной в цикле, равна, таким образом,

,

так как изменение внутренней энергии   в круговом процессе равно нулю (это функция состояния).

Напомним, что работа не является функцией состояния, иначе суммарная работа за цикл также была бы равна нулю.

При этом нагреватель потратил энергию  . Поэтому тепловой, или, как его ещё называют, термический или термодинамический коэффициент полезного действия тепловой машины (отношение полезной работы к затраченной тепловой энергии) равен

.

Вычисление работы и КПД в термодинамическом цикле

Работа в термодинамическом цикле, по определению, равна

,

где   — контур цикла.

C другой стороны, в соответствии с первым началом термодинамики, можно записать

.

Аналогичным образом, количество теплоты, переданное нагревателем рабочему телу, равно

.

Отсюда видно, что наиболее удобными параметрами для описания состояния рабочего тела в термодинамическом цикле служат температура и энтропия.

[править]Цикл Карно и максимальный КПД тепловой машины

Основная статья: Цикл Карно.

Цикл Карно в координатах T и S

Представим себе следующий цикл:

Фаза А→Б. Рабочее тело с температурой, равной температуре нагревателя, приводится в контакт с нагревателем. Нагреватель сообщает рабочему телу   тепла в изотермическом процессе (при постоянной температуре), при этом объём рабочего тела увеличивается.

Фаза Б→В. Рабочее тело отсоединяется от нагревателя и продолжает расширяться адиабатически (без теплообмена с окружающей средой). При этом его температура уменьшается до температуры холодильника.

Фаза В→Г. Рабочее тело приводится в контакт с холодильником и передает ему   тепла в изотермическом процессе. При этом объём рабочего тела уменьшается.

Фаза Г→А. Рабочее тело адиабатически сжимается до исходного размера, и его температура увеличивается до температуры нагревателя.

Его КПД равен, таким образом,

,

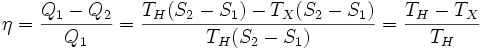то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо.

Можно показать, что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бо́льшим КПД.

Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно.