Двумерные дефекты]

Граница наклона

Основной дефект-представитель этого класса — поверхность кристалла. Другие случаи — границы зёрен материала, в том числе малоугловые границы (представляют собой ассоциации дислокаций), плоскости двойникования, поверхности раздела фаз и др.

Трёхмерные дефекты

Объёмные дефекты. К ним относятся скопления вакансий, образующие поры и каналы; частицы, оседающие на различных дефектах (декорирующие), например пузырьки газов, пузырьки маточного раствора; скопления примесей в виде секторов (песочных часов) и зон роста. Как правило, это поры или включения примесных фаз. Представляют собой конгломерат из многих дефектов. Происхождение — нарушение режимов роста кристалла, распад пересыщенного твердого раствора, загрязнение образцов. В некоторых случаях (например, при дисперсионном твердении) объемные дефекты специально вводят в материал, для модификации его физических свойств.

Методы избавления от дефектов

Основной метод, который помогает избавляться от дефектов в кристалле — метод зонной плавки. Этот метод хорошо применим для кремния. Плавят малую часть кристалла, чтобы впоследствии перекристаллизовать расплав. Используют также просто отжиг. Дефекты при повышенной температуре обладают высоким коэффициентом диффузии. Вакансии могут выходить на поверхность, и поэтому говорят об испарении дефектов.

Полезные дефекты

При пластической деформации металлов (например, ковке, прокатке), генерируются многочисленные дислокации, по-разному ориентированные в пространстве, что затрудняет разрушение кристалла по сетке дислокаций. Таким образом увеличивается прочность металла, но в то же время снижается пластичность.

В искусственно выращенных рубинах, сапфирах для лазеров добавл

Постулаты Бора — основные допущения, сформулированные Нильсом Бором в 1913 году для объяснения закономерности линейчатого спектра атома водорода и водородоподобных ионов (формула Бальмера-Ридберга) и квантового характера испускания и поглощения света. Бор исходил из планетарной модели атома Резерфорда.

Постулаты

Модель атома Бора

• Атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.

• Электрон в атоме, не теряя энергии, двигается по определённым дискретным круговым орбитам, для которых момент импульса квантуется: 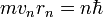 , где 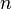  — натуральные числа, а 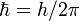  — постоянная Планка. Пребывание электрона на орбите определяет энергию этих стационарных состояний.

• При переходе электрона с орбиты (энергетический уровень) на орбиту излучается или поглощается квант энергии 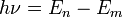 , где   — энергетические уровни, между которыми осуществляется переход. При переходе с верхнего уровня на нижний энергия излучается, при переходе с нижнего на верхний — поглощается.

Используя данные постулаты и законы классической механики, Бор предложил модель атома, ныне именуемую Боровской моделью атома^[1]. В дальнейшем Зоммерфельд расширил теорию Бора на случай эллиптических орбит. Её называют моделью Бора-Зоммерфельда.

Уровни энергии

Для получения энергетических уровней в атоме водорода в рамках модели Бора записывается второй закон Ньютона для движения электрона по круговой орбите в поле кулоновской силы притяжения:

где m — масса электрона, e — его заряд, Z — заряд ядра и k — кулоновская константа, зависящая от выбора системы единиц. Это соотношение позволяет выразить скорость электрона через радиус его орбиты:

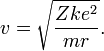
Энергия электрона равна сумме кинетической энергии движения и его потенциальной энергии:

Используя правило квантования Бора, можно записать:

откуда радиус орбиты выражается через квантовое число n. Подстановка радиуса в выражение для энергии даёт:

Комбинация констант

 ≈ 13,6 эВ

называется постоянной Ридберга. Она равна энергии связи электрона в атоме водорода в основном состоянии, т.е. минимальной энергии, необходимой для ионизации атома водорода в низшем (стабильном) энергетическом состоянии.

Экспериментальное подтверждение

Основная статья: Опыт Франка — Герца

В 1914 году Франк и Герц поставили опыт, подтверждающий теорию Бора: атомы разреженного газа обстреливались медленными электронами с последующим исследованием распределения электронов по абсолютным значениям скоростей до и после столкновения. При упругом ударе распределение не должно меняться, так как изменяется только направление вектора скорости. Результаты показали, что при скоростях электронов меньше некоторого критического значения удары упруги, а при критической скорости столкновения становятся неупругими, электроны теряют энергию, а атомы газа переходят в возбуждённое состояние. При дальнейшем увеличении скорости удары снова становились упругими, пока не достигалась новая критическая скорость. Наблюдаемое явление позволили сделать вывод о том, что атом может или вообще не поглощать энергию, или же поглощать в количествах равных разности энергий стационарных состояний.

Фа́зовый перехо́д (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий. С точки зрения движения системы по фазовой диаграмме при изменении её интенсивных параметров (температуры, давления и т. п.), фазовый переход происходит, когда система пересекает линию, разделяющую две фазы. Поскольку разные термодинамические фазы описываются различными уравнениями состояния, всегда можно найти величину, которая скачкообразно меняется при фазовом переходе.

Поскольку разделение на термодинамические фазы — более мелкая классификация состояний, чем разделение по агрегатным состояниям вещества, то далеко не каждый фазовый переход сопровождается сменой агрегатного состояния. Однако любая смена агрегатного состояния есть фазовый переход.

Наиболее часто рассматриваются фазовые переходы при изменении температуры, но при постоянном давлении (как правило равном 1 атмосфере). Именно поэтому часто употребляют термины «точка» (а не линия) фазового перехода, температура плавления и т. д. Разумеется, фазовый переход может происходить и при изменении давления, и при постоянных температуре и давлении, но и при изменении концентрации компонентов (например, появление кристалликов соли в растворе, который достиг насыщения).

Классификация фазовых переходов

При фазовом переходе первого рода скачкообразно изменяются самые главные, первичные экстенсивные параметры: удельный объём, количество запасённой внутренней энергии, концентрация компонентов и т. п. Подчеркнём: имеется в виду скачкообразное изменение этих величин при изменении температуры, давления и т. п., а не скачкообразное изменение во времени (насчёт последнего см. ниже раздел Динамика фазовых переходов).

Наиболее распространённые примеры фазовых переходов первого рода:

• плавление и кристаллизация

• испарение и конденсация

• сублимация и десублимация

При фазовом переходе второго рода плотность и внутренняя энергия не меняются, так что невооружённым глазом такой фазовый переход может быть незаметен. Скачок же испытывают их производные по температуре и давлению: теплоёмкость, коэффициент теплового расширения, различные восприимчивости и т. д.

Фазовые переходы второго рода происходят в тех случаях, когда меняется симметрия строения вещества (симметрия может полностью исчезнуть или понизиться). Описание фазового перехода второго рода как следствие изменения симметрии даётся теорией Ландау. В настоящее время принято говорить не об изменении симметрии, но о появлении в точке перехода параметра порядка, равного нулю в менее упорядоченной фазе и изменяющегося от нуля (в точке перехода) до ненулевых значений в более упорядоченной фазе.

Наиболее распространённые примеры фазовых переходов второго рода:

• прохождение системы через критическую точку

• переход парамагнетик-ферромагнетик или парамагнетик-антиферромагнетик (параметр порядка — намагниченность)

• переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата)

• переход жидкого гелия в сверхтекучее состояние (п.п. — плотность сверхтекучей компоненты)

• переход аморфных материалов в стеклообразное состояние

Современная физика исследует также системы, обладающие фазовыми переходами третьего или более высокого рода.

В последнее время широкое распространение получило понятие квантовый фазовый переход, т.е. фазовый переход, управляемый не классическими тепловыми флуктуациями, а квантовыми, которые существуют даже при абсолютном нуле температур, где классический фазовый переход не может реализоваться вследствие теоремы Нернста.

Динамика фазовых переходов

Как сказано выше, под скачкообразным изменением свойств вещества имеется в виду скачок при изменении температуры и давления. В реальности же, воздействуя на систему, мы изменяем не эти величины, а её объем и её полную внутреннюю энергию. Это изменение всегда происходит с какой-то конечной скоростью, а значит, что для того, чтобы «покрыть» весь разрыв в плотности или удельной внутренней энергии, нам требуется некоторое конечное время. В течение этого времени фазовый переход происходит не сразу во всём объёме вещества, а постепенно. При этом в случае фазового перехода первого рода выделяется (или забирается) определённое количество энергии, которая называется теплотой фазового перехода. Для того, чтобы фазовый переход не останавливался, требуется непрерывно отводить (или подводить) это тепло, либо компенсировать его совершением работы над системой.

В результате, в течение этого времени точка на