Потеря устойчивости за пределом пропорциональности материала стержня

Формулы (5.10) и (5.12) получены в предположении линейно упругой работы материала, что соответствует условию: , (5.16)

где - предел пропорциональности.

Отсюда вытекает условие, определяющее пределы применимости формулы Эйлера: (5.17)

Предельная гибкость , выше которой применима формула Эйлера, определяется соотношением: . Эта величина зависит от физико-механических характеристик материала, из которого изготовлен стержень. В частности, для стержней, изготовленных из стали 3: ( =200 МПа; Е = МПа); . Стержни, удовлетворяющие условию , называются гибкими.

В том случае, когда гибкость стержня ниже предельной ( ), потеря устойчивости происходит при напряжениях, превышающих предел пропорциональности, и применение формул (5.10), (5.11) может внести существенную погрешность в расчет.

Стержни средней гибкости ( ), широко распространенные в инженерной практике (в том числе и в практике строительства), могут терять устойчивость при напряжениях существенно ниже , , и расчет на устойчивость таких стержней необходим. Существующие теории расчета на устойчивость стержней средней и малой гибкости сводятся к двум концепциям.

Концепция Энгессера-Шенли.

Согласно этой концепции потеря устойчивости центрально сжатого стержня связывается с возможностью появления и развития смежной изгибной формы равновесия при монотонно возрастающей нагрузке, причем появление изгибной формы равновесия возможно уже при касательно-модульной нагрузке (рис. 5.4):

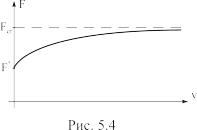
,(5.18) где - касательный модуль при критическом значении напряжения.

При прогибы формально обращаются в бесконечность. Однако критическим считается напряжение ,

Концепция Ясинского-Кармана.

Эта концепция основана на идее Эйлера о появлении смежной изгибной формы равновесия при неизменной нагрузке. Из условий равновесия системы сил внутреннего взаимодействия, соответствующей продольному изгибу, вытекают следущие соотношения:

; (5.20)

; , (5.21)

где (5.22) приведенный (редуцированный) модуль, соответствующий критическому напряжению.

S_t, S_c, I_t, I_c – статические моменты и моменты инерции растянутой и сжатой зон при продольном изгибе.

Особенно обширный опытный материал собрал Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в зависимости от гибкости для целого ряда материалов. Обобщение данных экспериментов позволило ему заметить, что для большинства конструкционных материалов эти завистимости близки к линейным, т.е. (5.23)

Исключения составляет чугун, для которого (5.24)

a, b, c – эмпирические коэффициенты. Данные об этих коэффициентах для различных материалов приведены в таблице 5.1 (см. приложение).

Если строить график для пластичного материала, то получим кривую, имеющую 2 участка (рис. 5.5). Аппроксимируя эту кривую на участке стержней малой гибкости ( ) прямой , а на участке стержней средней гибкости ( ) – прямой Ясинского , получим, например, для стержней, выполненных из строительной стали 3 ( МПа, МПа), график представленный на рис. 5.6.

Пользуясь графиками, приведенными на рис. 5.5., и рис. 5.6., можно определить критическое напряжение, а затем вычислить критическую силу по формуле: (5.25)

В тех случаях, когда внешняя нагрузка на конструкции не является осевой сжимающей силой F для конкретного стержня, но стержень при этом центрально сжат, по формуле (5.25) определяют критическое значение продольной силы для этого стержня – , а далее (зная зависимость продольной силы в стержне от нагрузки F из уравнения равновесия) – критическое значение нагрузки.

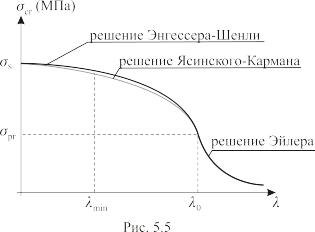
ПРИМЕР 5.1.

Требуется определить:

– критическое значение силы при которой сжатый подкос может потерять устойчивость, т.е. когда

– нормальное напряжение в растянутом стержне , возникающее от внешней силы .

Стержни и выполнены из стальных труб (сталь-3) с наружным диаметром см, и внутренним диаметром см. тогда .

РЕШЕНИЕ

1.Предварительные вычисления. Длина стержня см

2. Определим гибкость стержня ВС, предполагая одинаковое (шарнирное) закрепление концов стержня в обоих главных плоскостях , т.е. .

Сначала определим осевой момент инерции для трубчатого сечения :

Площадь поперечного сечения:

Радиус инерции сечения:

Тогда гибкость

3.Определим критическую сжимающую силу для подкоса ВС: т.к. гибкость (для стали 3), критическую силу определяем по формуле Ясинского (5.23) и (5.25). Из табл. 5.1 для Ст.3 находим

4.Вырежем узел "В" и из уравнений равновесия установим связь между силой F и продольной силой в подкосе (рис. 5.7 б).

Знак "минус" показывает сжимающий характер продольной силы в подкосе.

Отсюда выразим :

Найдем критическое значение силы : кН.

5.Определим нормальное напряжение в растянутом стержне АВ по формуле:

Для этого из уравнения равновесия найдем силу N_АВ:

Отсюда находим – кН.

Определяем кПа.

ПРИМЕР 5.2.

Требуется: Определить критическую силу и критическое напряжение в поперечном сечении сжатой стойки, изображенной на рис. 5.8. Поперечное сечение – на рис. 5.8 б.

Нижний конец бруса защемлен в обоих главных плоскостях. Закрепление верхнего конца принять: относительно оси "Z" –шарнирное, относительно оси "Y" – жесткое защемление. Материал – сталь 3, кПа.

РЕШЕНИЕ

1. Определяем величины главных центральных моментов инерции поперечного сечения стержня

2. Площадь поперечного сечения

3. Главные радиусы инерции -

4. Определим гибкости в обоих главных плоскостях –

5. Критическую силу определяем по большей гибкости

Т.к. (для Ст.3), критическую силу определяем по формуле Эйлера, в которой вместо I_min подставим .

кН

6. Определим критическое напряжение: МПа << 200

Критическое напряжение значительно меньше предела пропорциональности для Ст.3, равного 200 МПа, что подтверждает правомерность использования формулы Эйлера.

ПИМЕР 5.3.

Требуется.

Определить критическое значение интенсивности распределенной нагрузки , при которой деревянная сжатая стойка ВС может потерять устойчивость (рис. 5.9). При этом принять: кПа, .

РЕШЕНИЕ

1.Определим критическое значение продольной силы для стержня ВС. Оба конца стержня закреплены шарнирно, значит . а) Определим минимальный момент инерции сечения

см⁴

см⁴

I_z < I_y , значит I_z = I_min = 144 см⁴.

б ) Определим минимальный радиус инерции сечения –

.

в ) Определим гибкость стержня:

г ) По таблице 5.1 находим предельную гибкость стержня из дерева – =110. Так как гибкость 173 > ₀ = 110, то критическую силу определяем по формуле Эйлера:

2. Из уравнения равновесия, М_А = 0 , установим связь между интенсивностью распределенной нагрузки q и сжимающей силой R_c=|N_BC|.

3.Определяем критическое значение интенсивности нагрузки q:

Ответ: q_cr = 1,75 кН/м.

ПРИМЕР 5.4.

Требуется:

Определить критическую силу F_cr для сжатого стержня, показанного на рис. 5.10. Материал стержня – Ст.3, сечение составлено из 4-х неравнополочных уголков 63х40х5мм. (ГОСТ 8510-86), ₀=100.

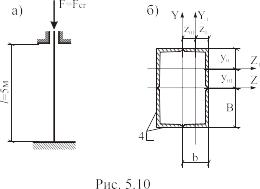
РЕШЕНИЕ

1. Определим минимальный радиус инерции сечения:

а ) Определим главные центральные моменты инерции.

Из таблицы сортаментов для прокатных неравнополочных стальных уголков для уголка № 63х40х5 мм. выписываем:

I_z1= 19,9 см⁴; y₀=2,08 см.

I_y1= 6,3 см⁴; z₀= 0,95 см.

b= 4 см; А₁= 4,98 см².

В=6,3 см.

Проводим оси симметрии всего сечения У и Z и центральные оси отдельных уголков У_i и Z_i (рис. 5.10),

Вычисляем расстояния от общих осей У и Z до осей У₁ и Z₁:

y₀₁ = B – y₀ = 6,3 – 2,08 = 4,22 см.

z₀₁ = b – z₀ = 4 – 0,95 = 3,05 см.

Учитывая наличие осей симметрии, определяем главные центральные моменты инерции всего сечения:

Так как оси Z и У являются осями симметрии, центробежный момент инерции равен нулю. ( I_zy=0). Значит найденные I_z и I_y – главные центральные моменты инерции, при этом I_y<I_z. Значит – I_min = I_y =210,52 см⁴.

б ) Определяем минимальный радиус инерции сечения:

2. Определяем гибкость при =0,5 (обаконца стержня защемлены):

3. Определяем критическое напряжение и критическую силу.

Так как гибкость =77<₀=100 (для стали 3), критическую силу определяем по формуле Ф. Ясинского, при коэффициентах – а=310 МПа, в=1,14 МПа.

Ответ: F_cr=442,7 кН.