Устойчивость. Понятие об устойчивости форм равновесия

При F=Fcr исходная форма равновесия стержня становится неустойчивой (рис. 5.1.б), и снятие возмущения не приведет к восстановлению исходной формы равновесия. При F>Fcr любое возмущение приводит систему к новой криволинейной форме равновесия, которая может оказаться устойчивой (рис. 5.1.в).

В целях обеспечения надежности работы конструкции в расчет водится допускаемое значение нагрузки F_adm: ,

где к_st>1-коэффициент запаса устойчивости.

Коэффициент запаса устойчивости принимается несколько большим, чем коэффициент запаса прочности (к_st>к),

Формула Эйлера для критической силы.

Согласно методу Эйлера исследуется возможность существования, наряду с исходной, другой формы упругого равновесия, порожденной возмущениями.

Т акой формой в рассматриваемой задаче является изгибная (рис. 5.2), и при ее описании в силу малости возмущений, можно воспользоваться приближенным дифференциальным уравнением оси изогнутой балки.

Так как в данном случае 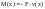, то (5.2) преобразуется виду: , (5.3)

где .

Пусть EI(x)=EI=const. Тогда уравнение (5.3) – линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общий интеграл этого уравнения имеет вид: , (5.4)

где А, В – постоянные интегрирования. Для определения А, В необходимо использовать кинематические граничные условия, которые в данном случае запишутся следующим образом:

x=0, а) x=l, б)

Подставляя а) в (5.4) получим В=0.

Из б) следует: Asinkl=0 (5.5)

Так как А 0 (из условия существования возмущенной формы), то из (5.5) следует уравнение: sinkl=0

Корни трансцендентного уравнения (5.6) (исключая тривиальный kl=0) определяют критические значения нагрузки, при которых возможно существование изгибной формы равновесия:

Отсюда при к получаем: , n=1,…,

Соотношение (5.7) определяет бесконечный ряд критических значений нагрузки, соответствующим различным формам изгиба стержня в результате потери устойчивости. Однако практическое значение имеет только первая форма, соответствующая минимальной критической силе

В том случае, когда на деформацию стержня не наложены какие-либо дополнительные ограничения, возмущенная форма равновесия реализуется в плоскости минимального сопротивления изгибу, и критическое значение силы равно: (5.8)

При этом возмущенная форма равновесия (первая собственная форма) соответствует полуволне синусоиды: волне, то в общем случае

где - приведенная длина стержня (длина шарнирноопертого стержня, теряющего устойчивость при той же критической силе, что и заданный); - коэффициент приведения длины. Величины коэффициентов приведения, соответствующих схемам а) - г), приведены на рис. 5.3.

Критическое напряжение. Проверка устойчивости стержня

Критическое напряжение потери устойчивости по формуле Эйлера находится путем деления величины критической силы, определенной по (5.10) на площадь сечения A_br (без учетвозможных ослаблений сечения): (5.11)

Обозначим – – минимальный радиус инерции сечения; – гибкость стержня.

Преобразуя (5.11) используя эти обозначения, получим: , (5.12)

Величина называется расчетным сопротивлением по устойчивости. Условие устойчивости центрально сжатого стержня можно записать в виде (5.13)

Условие устойчивости также может быть записано по отношению к нагрузке: , (5.14)

где F_adm – допускаемая нагрузка.

При более сложном характере нагружения условия устойчивости запишутся по отношению к параметру загружения. При однопараметрическом нагружении (все нагрузки пропорциональны одному параметру Р₀) условие устойчивости имеет вид: , (5.15) где P_0cr – критическое значение параметра нагружения.