Учет влияния продольной силы при изгибе с кручением

При использовании принципа суперпозиции наличие в числе внутренних силовых факторов продольной силы N приведет лишь к корректировке соотношения для нормальных напряжений в сечениях. Для стержней круглого сплошного и трубчатого поперечных сечений формула для максимального по модулю нормального напряжения в опасной точке контура имеет вид:

(4.32)

Условие прочности, например, по третьей теории прочности запишется следующим образом:

Д ля решения проектной задачи подбора сечения из условия прочности можно в данном случае рассмотреть следующий алгоритм:

1. На начальном этапе сечение подбирается без учета продольной силы по методике, изложенной ранее. Подобранные размеры (номер в сортаменте) округляется с учетом требований ГОСТ-ов в большую сторону.

2. Проводится проверка прочности подобранного на первом этапе сечения с учетом влияния продольной силы. При невыполнении условия прочности делаются шаги в сторону увеличения сечения вплоть до выполнения условия прочности. На случай, если шаг принят слишком большим и скорректированное сечение недонапряжено больше 5%, в алгоритме необходимо предусмотреть возврат и уменьшение шага корректировки.

ПРИМЕР 4.6

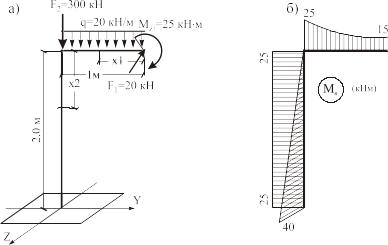
Дано: Стержень с ломаной осью загружен силами, как показано на рис. 4.20 а.

Требуется: Подобрать диаметр стержня трубчатого сечения при следующих условиях: R = 200 МПа, с = d_int/d_ext = 0,8.

РЕШЕНИЕ

1. Строим эпюры внутренних усилий, используя приведенную в предыдущем примере методику. (Для каждого грузового участка используем местную систему координат).

1-й участок, 0 x₁ 1м. (4.21).

Изгибающие моменты:

М_Z = M_Z1+q =15+20 ;

x₁=0; М_Z=15кНм (растягиваются верхние волокна).

x₁=0,5м; М_Z=15+20 =17,5кНм.

x₁=1м; М_Z=15+20 =25 кНм.

М_Y=F₁x₁=20 x₁;

x₁=0; М_Y=0;

x₁=1м; М_Y=201м=20 кНм (растягиваются передние волокна).

Крутящие моменты – M_x=M_t=0

Продольные силы – N=0

2-й участок; 0 x₂ 2м.

Изгибающие моменты:

М_Z=–М_Z1–q1 = –15–2010,5= –25 кНм.

М_Y=F₁х₂=20х₂;

х₂=0; М_Y(0)=0;

х₂=2м; М_Y(2)=40 кНм (растягиваются передние волокна)

Крутящие моменты:

M_X=M_t=F₁1м=20 кНм.

Продольная сила:

N= –300–q1м= –320 кНм

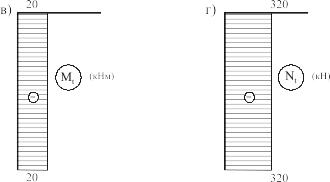
По полученным значениям строим эпюры М_в, М_t и N (рис.4.20 б, в и г).

2. Выясняем опасное сечение. Из визуального анализа эпюр видно, что наиболее опасным является сечение в нижней части 2-го участка – т.е. сечение у жесткой заделки.

Выпишем все внутренние усилия в указанном опасном сечении:

М_y=40 кНм; M_Z=25 кНм; М_t=20 кНм; N=320 кН.

3. Определим общий изгибающий момент M_B.

М_в= кНм.

4. Определим расчетный момент по 3-й гипотезе прочности.

кНм.

5. Подбор диаметра сечения стержня ведем по методу последовательных приближений, т.к. в опасном сечении, кроме изгибающего и крутящего моментов, имеется продольная сила N=320 кН.

а) В первом приближении определим диаметр стержня без учета продольной силы по аналогии с предыдущим примером 4.6.

Из условия равенства W = W_тр для кольцевого сечения находим наружный диаметр трубы [11]:

,

По таблице сортаментов для круглого горячекатаного стального проката (ГОСТ 2590-88) примем ближайший больший диаметр: d_ext = 165 мм = 16,5 см.

Проверим прочность по 3-й гипотезе прочности, по формуле (4.24), но уже с учетом влияния нормальной силы N на нормальное напряжение .

Предварительно определим площадь поперечного сечения А и осевой момент сопротивления W при принятом диаметре d_ext=16,5см.

Определяем суммарное нормальное напряжение:

=223,08 МПа.

Определяем касательное напряжение от крутящего момента:

Полученные напряжения  и  подставим в условие прочности

Имеет место перенапряжение, определим его в процентах:

-(недопустимо)

Выполним 2-е приближение проверим прочность следующего большего диаметра по таблице ГОСТа, d_ext=170 мм=17 см.

Повторим расчет при этом диаметре:

10^-6м³

Определяем суммарное нормальное напряжение

=202,73 Мпа.

Определяем касательное напряжение от крутящего момента:

МПа

Полученные напряжения  и  подставим в условие прочности (

МПа > R

Имеет место перенапряжение, определим его в процентах:

(недопустимо)

Имеет место недопустимое перенапряжение.

Повторим расчет при , d_ext=175 мм=17,5 см:

10^-6м³

Определяем суммарное нормальное напряжение:

=186,79 МПа.

Определяем касательное напряжение от крутящего момента:

МПа

Полученные напряжения  и  подставим в условие прочности

МПа>R

Условие прочности выполняется с незначительным запасом.

Окончательно принимаем: d_ext=17,5см=175 мм. d_int=,8d_ext=0,8175=140 мм.